Усталостное разрушение является результатом многократно повторяющихся упругих и пластических деформаций, распределенных неравномерно по объему детали. Высокий уровень форсирования современных дизелей определяет тепловые и механические нагрузки, действующие на поршень, что приводит к его преждевременному разрушению. По данным исследования в работе [7] форсирование двигателя ЯМЗ-240 по мощности свыше 30 % с помощью газотурбинного наддува (ГТН) привело первоначально к массовому выходу поршней из строя по причине образования трещин на кромке камеры сгорания (КС). Точно так же при форсировании дизелей Д-240 у поршней с камерой сгорания типа ЦНИДИ на кромке КС уже через 4000 часов появились трещины [3, 12].
В связи с этим возникает закономерный вопрос, насколько уменьшается долговечность поршней при наличии трещин и какими моделями следует пользоваться при ее расчете.
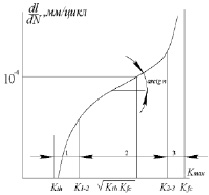
Рис. 1. Диаграмма усталостного разрушения (схема): 1, 3 – области низких и высоких скоростей роста трещины; 2 – область справедливости формулы Париса
Цель исследования – провести анализ предложенных в настоящее время моделей усталостного роста трещин при нагружении детали переменной нагрузкой и определить приемлемую из них для расчета долговечности поршня при наличии трещины на кромке камеры сгорания.
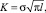(1)
где σ – напряжения вблизи вершины трещины; l – длина трещины.
По существу, коэффициент К характеризует концентрацию напряжений у вершины трещины и зависит от действующей нагрузки, геометрии детали, размера трещины, а в случае и анизотропного материала – еще и от характеристики упругости. Весь процесс роста трещины условно делят на несколько участков (рис. 1) [13, 14, 17].
Для первого участка характерны низкие скорости роста трещины. Второй участок – прямолинейный; он характеризуется средними скоростями увеличения размера трещины. На этих участках трещина относится к классу устойчивых. Третий участок отличают высокие скорости и неустойчивый рост трещины.
Для аналитического описания скорости роста трещины предложено более 60 формул [4, 6]. Все эти зависимости практически следуют из формулы П. Париса и Эрдогана [4], которая основана на том, что все процессы, происходящие в вершине трещины, а также скорость развития длины трещины Ltr от числа циклов N dLtr/dN (ее рост) зависят от коэффициента концентрации напряжений.
Эта формула записывается в следующем виде:
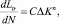(2)
где Ltr – длина трещины; С – коэффициент, зависящий от свойств материала, частоты и среднего напряжения; n – константа материала; ΔK = Kmax – Kmin перепад (изменение коэффициента интенсивности напряжений в цикле); N – число циклов.
Многочисленные экспериментальные данные хорошо подтверждают эту формулу, причем показатель степени n для различных материалов находится в пределах от 2 до 7 (наиболее часто n = 3…4) [4, 5, 6, 11]. Чем больше показатель степени n, тем более хрупкое состояние материала наблюдается при испытании.
Существует также модификация записи формулы Париса. Эта формула выглядит следующим образом [11]:
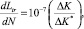мм/цикл, (3)
где ΔK* – граничное значение размаха ΔK, соответствующее режиму нагружения, для которого величина местного напряжения на кромке трещины равна пределу текучести σ0,2 материала.
Формула Париса описывает средний (линейный) участок полной диаграммы усталостного разрушения, которая в большинстве случаев имеет S-образный вид (рис. 1). Эта диаграмма порождает характеристики трещиностойкости при циклическом нагружении.
Долговечность каждого участка также различна. Долговечность первого участка составляет примерно 15…25 %, второго – 65…75 % и третьего несколько десятков процента. Таким образом, самым долговечным является второй участок диаграммы роста трещины. Этот участок заключен между пороговым КИН (величина местного напряжения на кромке трещины меньше предела текучести σ0,2 материала) ΔKth и его граничным значением ΔK*. Собственно, отношение между этими коэффициентами составляет основу прогнозирования остаточного ресурса детали [1].
Порог развития усталостной трещины ΔKth представляет собой минимальное значение КИН, определяющее безопасную границу уровня переменных напряжений для тел с трещинами. Значения порогов ΔKth зависят от типа металла и его механических свойств (в первую очередь от предела текучести), от коэффициента асимметрии цикла r, толщины образца, частоты нагружения. С ростом предела текучести уменьшается и трещиностойкость [15]. Значения ΔKth для зарубежных алюминиевых сплавов показаны на рис. 2.
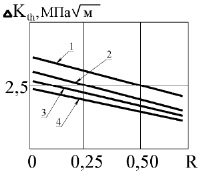
Рис. 2. Зависимость порогов ΔKth от R для зарубежных алюминиевых сплавов (в скобках дана марка отечественных сплавов): 1 – RR58 (АК-4) [Батиас и др., 7]; 2 – 7075-Т651 (В95); 3 – 7075-Т7351 (В95); 4 – 2L93; 2, 3, 4 – по данным Биверса [8]
По величине КИН судят об устойчивости или неустойчивости трещины. Трещина называется устойчивой, если она не увеличивается или ее рост линейно зависит от нагрузки.
Проблема оценки долговечности детали с трещиной заключается в том, чтобы правильно определить геометрию трещины, подсчитать критический размер и располагать информацией о закономерностях ее роста. Для оценки скорости роста трещины и увеличения ее начального размера до критической величины чаще всего используют расчетные модели, в основе которых лежит описание поведения трещины в рамках линейной теории упругости. Между тем установлено, что напряжения у вершины трещины обычно превышают предел текучести и обуславливают локальную пластическую зону; ее размеры по сравнению с трещиной малы. Учет малой зоны пластичности у вершины трещины осуществляется поправочным коэффициентом, предложенным Ирвином [2, 4, 9, 11].
Ирвин и Орован заметили [4], что в металле перед трещиной образуются пластические деформации и во время распространения трещины энергия расходуется на образование зоны пластической деформации при вершине распространяющейся трещины. Материал при вершине трещины не будет готов к расцеплению, пока напряжения и деформации не станут достаточно велики, чтобы стало возможно образование трещины. К моменту, когда возникнет такая ситуация, образуется довольно большая зона пластической деформации. Трещина может расти только в том случае, если в процессе ее роста выделяется достаточно энергии, чтобы совершить работу по образованию зоны пластической деформации при новой вершине трещины.
В.К. Румб и В.В. Медведев [13, 14] предлагают определять радиус зоны пластической деформации r в случае объемного напряженного состояния по зависимости
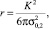(4)
где σ0,2 – предел текучести материала.
С учетом радиуса пластической зоны эффективная длина трещины, эквивалентная фактической поврежденности материала, составит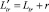 
.
Таким образом, при расчете остаточного ресурса зону пластической деформации у вершины трещины можно учитывать достаточно просто, если длину трещины заменить ее эффективной величиной. Однако если радиус зоны пластической деформации велик, то погрешность оценки долговечности становится большой. В этом случае требуется использовать методы упругопластического разрушения.
Согласно работам Е.М. Морозова [9] предполагается, что если Kmax < Kth, то трещина не растет. Отметим, что развитие трещины возможно при наличии пластической деформации, когда КИН равен Kfc, и при хрупком разрушении KIC. Поскольку в процессе циклического нагружения возможно изменение механических свойств материала, то вообще Kfc < KIC (например, Kfc = (0,8...0,9)KIC). Коэффициент KIC представляет собой вязкость разрушения (механическая характеристика материала, оценивающая его сопротивление распространению трещины при хрупком разрушении) для трещины определенного типа деформации (отрыв, поперечный сдвиг, продольный сдвиг). Тем не менее экспериментальное определение этих характеристик достаточно сложно, потому допустимо считать что Kfc = KIC (или KC для данной толщины).
Анализу упругих напряженных состояний в зоне концентрации посвящено большое число фундаментальных работ по решению краевых задач теории упругости (Н.И. Мусхелишвили, Г.Н. Савин, Р. Петерсон, Г. Нейбер и др.). Обобщение результатов этих работ, а также многочисленных экспериментальных исследований, позволило получить обширную справочную информацию о важнейших параметрах концентрации напряжений, входящих в расчеты прочности и ресурса – теоретических коэффициентов концентрации и градиентах напряжений [16].
Отметим также, что использование МКЭ для решения задач механики разрушения используется достаточно широко [8].
Результаты исследования и их обсуждения
Совершенно очевидно, что скорость распространения усталостной трещины не в такой степени определяется такими свойствами материала, как предел прочности или предел текучести. На практике экспериментальные точки на диаграмме dLtr/dN от ΔK имеют большой разброс в значениях. Это означает, что любое выражение, полученное эмпирическим путем, может обладать определенными достоинствами (в особенности, когда оно применимо к ограниченному числу данных для небольшого количества сплавов).
Результаты расчета реально представлять в виде графика dLtr/dN от КИН. При известных условиях нагружения расчет количества циклов, необходимых для роста трещины, может быть сведен к интегрированию выражения
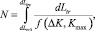(5)
где Ltr0 – минимальный размер трещины, поддающийся обнаружению; Ltr c – ее критическая длина.
Стоит отметить, еще один критерий разрушения – критерий раскрытия трещины (КРТ или COD), предложенный одновременно Уэллсом, Коттрелом и Баренблатом [4]. КРТ – экспериментальная характеристика, зависящая от температуры, скорости деформирования и объемности напряженного состояния. Использование данного критерия основано на допущении, что разрушение наступает, когда раскрытие трещины в вершине достигает некоторого критического значения, характерного для рассматриваемого материала. Использование этого критерия связано со многими трудностями, а измерение КРТ технически осуществить нелегко [4, 6].
Согласно критерию Гриффитса [4], рост трещины будет происходить в том случае, если освобождаемая при этом энергия достаточна для обеспечения всех затрат энергии, связанных с ростом трещины. Таким образом, в условиях плоской деформации должно выполняться следующее условие:
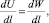(6)
где U – упругая энергия, а W – энергия, необходимая для роста трещины.
В то же время при расширении трещины освобождается потенциальная энергия, которая может быть израсходована на разрушение.
Из формулы (6) после подстановки значений U и W Гриффитс предложил зависимость для определения критического напряжения ps при расширении трещины:
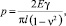
где p – величина напряжения в вершине трещины; E – модуль упругости материала; γ – плотность поверхностной энергии, т.е. работа, необходимая для образования единицы свободной поверхности; l – длина трещины; ν – коэффициент Пуассона.
Эта формула при заданной длине l определяет критическое напряжение p = ps, приводящее к расширению трещины, так как с увеличением длины l критическое напряжение уменьшается и далее происходит быстрое (лавинное) распространение трещин.
Выводы
Обзор моделей роста усталостных трещин показывает, что для оценки остаточной долговечности поршня при наличии трещины можно воспользоваться зависимостью Париса или ее модифицированным видом [4]. Пластические свойства материала поршня из алюминиевого сплава можно учесть с помощью введения поправки на критическую длину трещины или по формуле (4).
Библиографическая ссылка
Гоц А.Н., Глинкин С.А. ОБЗОР МОДЕЛЕЙ УСТАЛОСТНОГО РАЗРУШЕНИЯ ПРИ ЦИКЛИЧЕСКОМ НАГРУЖЕНИИ // Фундаментальные исследования. – 2016. – № 9-3. – С. 478-482;URL: https://fundamental-research.ru/ru/article/view?id=40769 (дата обращения: 23.11.2024).