Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ануфриев Д.П. 1 Холодов Ю.В. 1

---

1 ГАОУ АО ВО «Астраханский государственный архитектурно-строительный университет»

Актуальность статьи определяется необходимостью решения задачи управления жилищным строительством в условиях рыночных отношений, выделения факторов, позволяющих обеспечить устойчивый рост жилищного строительства региона на основе математических моделей, отражающих причинно-следственные связи. Для математического моделирования бизнес-процесса управления строительным комплексом предложено использовать математическое моделирование на базе нелинейных моделей математической физики. В статье методами нелинейной динамики проанализированы взаимоотношения дольщиков и банка, предоставившего ипотечный кредит. В зависимости от величины процентной ставки получена динамика возврата заемных средств и проведена количественная оценка вероятностей рисков семьи при выплате ипотечного кредита. Теоретические выкладки подтверждены мониторинговыми социологическими исследованиями, проведенными в Астраханской области в 2012–2015 гг.

Статья в формате PDF

0 KB

нелинейная динамика

вероятности рисков

связанные с выплатой заемных средств

функция распределения динамики выплат по ипотечному кредиту

процентная ставка по ипотечному кредиту

1. Ануфриев Д.П. Жилище как элемент социально-экономической системы региона (опыт прикладного исследования) // Вестник МГСУ. – 2014. – № 2. – С. 187–196.

2. Ануфриев Д.П. Жилищно-коммунальный комплекс в социально-экономической системе Юга России (на примере Астраханской области) // Известия Волгоградского государственного технического университета. – 2014. – № 24 (151). – Т. 19.

3. Ануфриев Д.П. Качество жизни населения как индикатор новой индустриализации (на примере Астраханской области) / Д.П. Ануфриев, Е.В. Каргаполова, И.И. Потапова // Вестник Омского университета. – Сер. Экономика. – 2015. – № 3. – С. 232–238.

4. Ануфриев Д.П. Качество жизни населения: оценка состояния и пути улучшения / В.А. Алешкин, Л.В. Боронина, Е.В. Каргаполова, Н.В. Купчикова, О.В. Рубальский, П.Н. Садчиков; под общ. ред. Л.В. Борониной. – Волгоград: Волгоградское научное изд-во, 2015. – 156 с.

5. Ануфриев Д.П. Оценка развития строительного рынка / С.Н. Коннова, А.И. Алиева, Е.В. Каргаполова // Инженерно-строительный вестник Прикаспия. – № 3(9). – С. 33–39.

6. Ануфриев Д.П. Регион: пространство смыслов и содержание / Д.П. Ануфриев, А.Ю. Арясова, Е.О. Беликова, Н.В. Дулина, И.Н. Наумов, В.А. Парамонова, М.А. Симоненко, В.В. Токарев. – Волгоград: Волгоградское науч. изд-во, 2013. – 294 с.

7. Астрводоканал Тарифы 2015 [электронный ресурс]. – Режим доступа: http://www.astrvodokanal.ru/viewpage.php page_id = 115; (дата обращения: 02.01.2016).

8. Корн Г., Корн Т. Справочник по математике. – М.: Изд-во «Наука», 1974. – 831 с.

9. Малинецкий Г.Г., Потапов А.Б. Современные проблемы нелинейной динамики. – М.: Едиториал УРСС, 2002. – 360 с.

10. Прожиточный минимум в Астраханской области стал меньше почти на 3,8 %. ИА REGNUM [электронный ресурс]. – Режим доступа: http://regnum.ru/news/economy/2000823.html, (дата обращения: 02.01.2016).

11. Ризниченко Г.Ю. Математические модели в биофизике и экологии. – М.-Иж.: ИКИ, 2003. – 184 с.

12. Тарифы на электроэнергию в Астраханской области 2015. Интернет-портал Энерго-Консультант, [электронный ресурс]. – Режим доступа: http://www.energo-consultant.ru/sprav/tarifi_na_elektroenergiuy_na_2015_god/tarifi_na_elektroenergiyu_v_Astrahanskoi_oblasti15; (дата обращения: 02.01.2016).

13. Anufriev, D. Modernization of regional housing complex: Imbalances and contradictions, advantages, issues, challenges / E. Kargapolova, L. Boronina // International Congress. Energy and Environment Engineering and Management (Paris, 22-24 July 2015). – Р. 282–284.

14. Anufriev, D. Transformation Of Housing And Communal Services Of Modern Russia / D. Anufriev, E. Kargapolova, L. Boronina, V. Svintsov, R. Muhanov // Advanced Materials Research. – 2015. – Vol. 1073–1076. – Р. 2602–2605.

В настоящее время одной из основных форм обеспечения населения жильем является долевое участие в жилищном строительстве. В основном это происходит с участием банковского капитала, в виде ипотечного кредитования. Лабораторией социально-психологических исследований Астраханского инженерно-строительного института под научным руководством Д.П. Ануфриева проведено мониторинговое социологическое исследование. Первая волна мониторинга была проведена в Астраханской области в декабре 2012 г. (N = 700), вторая – в марте 2013 г. (N = 690), третья – в ноябре 2013 г. (N = 700), четвертая – в апреле 2014 г. (N = 700), пятая – в ноябре 2014 г. (N = 600), шестая – в марте 2015 г. (N = 1200), седьмая – в ноябре 2015 г. (N = 1000). Технические параметры исследования следующие: исследование проводилось методом анкетирования по месту жительства; выборка стратифицированная, квотно-маршрутная; квотируемые признаки – пол, возраст, тип поселения; погрешность выборки – 3 %. Анализ данных включал изучение линейных распределений, осмысление таблиц сопряженности.

По результатам седьмой волны мониторингового социологического исследования, проведенного лабораторией социально-психологических исследований Астраханского инженерно-строительного института, 41,2 % астраханцев считают, что улучшение деятельности регионального жилищно-строительного комплекса зависит от развития банковского сектора. По обобщенным данным семи волн планируют для улучшения жилищных условий участие в ипотечной программе 11–17 % астраханцев [1–6, 13, 14].

Оплата жилья, приобретенного по ипотеке, пропорциональна ежемесячному доходу семьи. Так, по результатам седьмой волны мониторинга доступность приобретения жилья напрямую зависит от доходов семьи, складывающихся из зарплат работающих. Так считают 52,6 % опрошенных и ставят среднюю заработную плату работающих на первое место среди других факторов, влияющих на доступность приобретения жилья.

Погашение процентной ставки ипотечного кредита и основного долга перед банком происходит из дохода, остающегося в распоряжении семьи, и напрямую связано с величиной и сроком самого ипотечного кредита. Так, 27,3 % опрошенных считают, что доступность приобретения жилья зависит от процентной ставки по ипотечному кредиту, 20,9 % астраханцев – от процента первоначального взноса по ипотеке, 17,7 % респондентов – от ее срока.

Нелинейная динамическая модель ипотечного кредитования

Одна из важнейших задач управления в строительном комплексе – это рациональное распределение ограниченных ресурсов (финансовых, материальных, кадровых), поэтому большинство практических задач хозяйственной деятельности связано с выбором наилучшего варианта поведения, т.е. с оптимальным управлением в условиях существующих ограничений.

На основе анализа существующих подходов математического моделирования бизнес-процесса управления строительным комплексом предложено использовать математическое моделирование на базе нелинейных моделей математической физики (синергетический подход, макроуровень), при котором формируется система дифференциальных уравнений, связывающая небольшое количество независимых переменных. В результате решения этой системы определяется нелинейная функция, описывающая динамику процесса при минимальной детализации, либо вводится целевой функционал на системе ограничения параметров, определяются его локальные экстремумы и на основе их анализа делаются выводы о стационарном состоянии системы.

Для устойчивого развития строительной отрасли региона на продукцию отрасли должен постоянно присутствовать платежеспособный спрос. Самое массовое жильё региона – это жильё экономкласса, которое в основном приобретается семьёй по ипотеке. Ипотечное жилищное кредитование является одним из наиболее развивающихся направлений в банковской системе, что обуславливает необходимость анализа динамики данного явления. Скорость оплаты жилья, приобретенного по ипотеке, будет пропорциональна ежемесячному доходу семьи. Погашение процентной ставки ипотечного кредита и основного долга перед банком происходит из дохода, остающегося в распоряжении семьи, и напрямую связано с величиной и сроком самого ипотечного кредита. Тогда дифференциальное уравнение, описывающее данный процесс, будет иметь вид

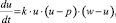(1)

где du/dt – скорость погашения ипотечного кредита; u – совокупный доход семьи; p – затраты семьи на удовлетворение физиологических потребностей членов семьи, определяемых прожиточным минимумом, сложившимся в регионе, и затратами на содержание жилья, включая жилищно-коммунальные услуги и выплаты по ипотеке; w – общая сумма, выплаченная банку за предоставление ипотечного кредита. Величина (u – p) – доход семьи, остающийся в её распоряжении, k – коэффициент пропорциональности. Ежемесячные затраты семьи p связаны следующим соотношением:

p = N•u_min + u_ky + u_б, (2)

здесь N – число членов семьи; umin – минимальный прожиточный уровень в регионе на одного человека [10]; uky – стоимость коммунальных услуг [7, 12]; uб – ежемесячные выплаты по ипотечному кредиту и процентам по нему.

Отметим, что данное уравнение по своей форме, аналогично логистическому уравнению математической экологии, описывающему численность популяции в условиях ограниченной экологической ниши [11], и относится к основным базовым моделям нелинейной динамики [9].

Предложенное дифференциальное уравнение решается аналитически [8]. Разделив переменные, в уравнении (1) получим

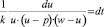, (3)

и, разлагая левую часть уравнения (3) на сумму элементарных дробей, получаем интегрируемое дифференциальное уравнение:

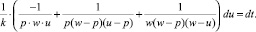
Коэффициент пропорциональности k и постоянную интегрирования С найдем из граничных условий. Постоянная интегрирования С находится из условия: доход семьи в начальный момент времени t = 0 состоит из ежемесячной зарплаты супругов u(0) = uз, а k из граничного условия: семья полностью выкупает квартиру в срок n лет, погасив ипотечный кредит и проценты по нему в объёме общей суммы равной w.

Таким образом, решение дифференциального уравнения (3) имеет вид

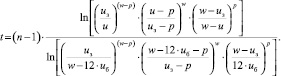(4)

Разрешить это уравнение относительно u(t) несколько затруднительно, поэтому исследуем его графически в прикладном пакете MATHCAD, в следующих координатах: u – ось ординат и t(u) – ось абсцисс.

Исследование динамики выплат семьи по ипотечному кредиту

Рассмотрим следующую задачу: оценим риски семьи по возврату ипотечного кредита в зависимости от процентной ставки банка при следующих условиях: годовой доход семьи составляет 1,0 млн руб. семья, состоящая из четырех человек, приобретает квартиру площадью 75 кв. метров по цене 43,(3) тыс. рублей за кв. метр.

Семья, состоящая из четырех человек – отца, матери и двоих детей, нами выбрана не случайно. Удовлетворение жилищных потребностей такой семьи, обеспечивающей простое воспроизводство населения, является индикатором нижней границы эффективности жилищно-строительного комплекса как социально-экономической системы. Необходимо отметить, что по данным седьмой волны мониторинга категория астраханцев, состоящих в браке, в меньшей степени готова улучшать свои жилищные условия путем ипотеки, чем состоящие в разводе и холостые (13,2 % против 21,3 и 15,2 % опрошенных). Также, несмотря на реализуемую в Российской Федерации программу материнского капитала, семьи без детей и с одним ребенком в большей степени выбирают путь ипотечного кредитования, чем семьи с двумя, а также тремя и более детьми (18,2 и 21,7 % опрошенных против 7,2 и 10,7 % респондентов). Кроме того, большая часть из опрошенных с одним ребенком (28,2 %) ответила, что их средний доход на каждого члена семьи ежемесячно составляет 5001–7000 руб., тогда как наибольшая часть опрошенных с двумя, а также тремя и более детьми (36,8 и 32,9 % соответственно) попадает в более низкодоходную группу – 3001–5000 руб. на каждого члена семьи ежемесячно. Таким образом, можно предположить, что риски семьи с двумя детьми значительнее, чем у семей без детей и с одним ребенком, и нуждаются в пристальном изучении.

Предположим, что на стадии готовности фундамента семья вносит первый взнос в размере 250 тыс. руб., из материнского капитала, оставшуюся сумму в 3 млн руб., семья покрывает за счет ипотечного кредита, взятого у банка на срок 10 лет. Численный эксперимент проведем для годовых банковских ставок в 7, 10 и 12 %, при постоянстве ежемесячных выплат банку. Общая сумма и годовые выплаты банку в зависимости от процентной ставки приведены в таблице.

Подставляя рассчитанные данные в соотношение (4), получим следующие графики. Сплошная линия, рассчитанная по формуле (4), показывает динамику расходов семьи, которая нормирована на общую сумму выплат банку. Пунктирная линия, которая также нормирована на общую сумму выплат банку, показывает динамику постоянных платежей банку по ипотечному кредиту. Заметим, что функции u7(n) и U7(n) (рис. 1), нормированные на соответствующую величину w, представляют собой интегральные функции распределения, и тогда по оси абсцисс отсчитывается вероятность погашения ипотечного кредита банку [8].

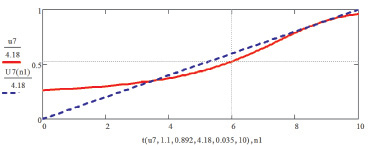
Рис. 1. Динамика выплат семьи при 7 % ставке за ипотечный кредит – сплошная линия, требуемая динамика банковских платежей – пунктирная линия, каждая из которых нормирована на общую сумму выплат банку

Как видно из рис. 1, в период, начиная с 4 года и до 8 года, у семьи возникают трудности с погашением ипотечного кредита. Пунктирная линия, характеризующая требуемую динамику банковских платежей, находится выше, чем сплошная линия, описывающая возможности выплат семьи. Разница в этом интервале между пунктирной и сплошной линиями будет равна вероятности риска задержек с выплатами ипотечного кредита семьёй и численно это значение составляет величину р7 % (6 лет) = 0,075 = 0,6 – 0,525, например, на шестой год выплат. Данное значение нетрудно получить, используя операцию трассировки графиков, содержащуюся в пакете MATHCAD.

Причем вероятность риска выплатами ипотечного кредита будет возрастать в зависимости от роста процентной ставки банка. Данный факт проиллюстрирован на графиках, представленных на рис. 2 и 3.

Вероятность задержек с выплатой ипотечного кредита при 10 % годовой ставки на седьмой год выплат составит следующую величину р10 % (6 лет) = 0,14 = 0,6 – 0,46. Аналогичная величина при 12 % ставке за ипотечный кредит равна р12 % (6 лет) = 0,21 = 0,6 – 0,39.

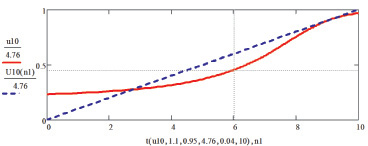
Рис. 2. Динамика выплат семьи при 10 % ставке за ипотечный кредит – сплошная линия, требуемая динамика банковских платежей – пунктирная линия, каждая из которых нормирована на общую сумму выплат банку

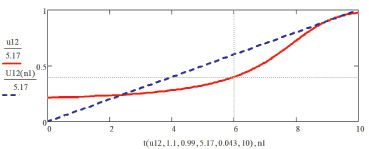
Рис. 3. Динамика выплат семьи при 12 % ставке за ипотечный кредит – сплошная линия, требуемая динамика банковских платежей – пунктирная линия, каждая из которых нормирована на общую сумму выплат банку

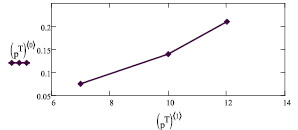
Рис. 4. Вероятности рисков семьи в зависимости от процентной ставки за ипотечный кредит

Объединяя полученные результаты в матрицу, первая строка – вероятности задержки с выплатой ипотечного кредита, вторая строка – процентные ставки за использование банковского кредита, построим зависимость вероятностей риска семьи от годовой ставки ипотечного кредита

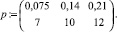
Таким образом, нелинейная модель позволяет количественно оценить риски семьи при погашении ипотечного кредита. Отмечено, что при 7 % ставке за ипотечный кредит в среднем 7,5 семей из 100 будут испытывать проблемы с погашением кредита в 3 млн рублей, взятых на десять лет у банка. При 10 % ставке каждая седьмая семья будет испытывать трудности с погашением кредита, а при 12 % ставке с этими трудностями встретится каждая пятая семья, конечно при заданном уровне семейных доходов. Естественно, здесь рассмотрены риски семьи, возникающие из-за внутрисемейных отношений.

Из графиков, представленных на рис. 1, 2 и 3, видно, что внутрисемейные риски увеличиваются по мере взросления детей и максимальные вероятности данных рисков приходятся на подростковый период детей. Возможно, в этот период детям трудно смириться с отсутствием многих так называемых «модных вещей», которые имеются у их сверстников и отсутствуют в их семье. И родителям очень трудно выдерживать психологическое давление со стороны подростков.

Важно отметить, что основной задачей участников ипотечного кредитования является своевременное погашение ипотечного кредита. В этом заинтересованы как участники долевого строительства, так и банк. В этой связи возможно банку выбрать более гибкую стратегию погашения ипотечного кредита как можно ближе к закономерности выплат семьи. Таким образом, банк существенно может снизить внутрисемейные риски погашения ипотечного кредита.

Выводы

1. Предложена нелинейная динамическая математическая модель, описывающая динамику выплат семьи в зависимости от доходов семьи, величины, срока и процентной ставки ипотечного кредита, цены квадратного метра, численности семьи и расходов семьи, направляемых на содержание жилья и членов семьи.

2. Модель также позволяет определить вероятность риска семьи по выплате ипотечного кредита. С учетом данного критерия проанализирована динамика выплат семьи в зависимости от процентной ставки, величины и длительности ипотечного кредита, численности семьи и от вложения материнского капитала и первоначального взноса.

3. Основные теоретические выводы, полученные в результате анализа нелинейной динамической модели, подтверждены результатами мониторинговых социологических исследований, проведенных в Астраханской области в 2012–2015 гг.

Библиографическая ссылка