Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ратушняк А.И. 1 Каргу Д.Л. 1 Чудновский Ю.А. 1 Шубин Д.А. 1 Гридин В.В. 1

---

1 ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны Российской Федерации

В представленной статье приведена разработанная линеаризованная математическая модель, описывающая динамику электрогидравлического привода ракеты-носителя. Модель состоит из передаточных функций его основных узлов. Предложено для оценивания качества функционирования электрогидравлических приводов в динамических режимах перейти от использования традиционных временных характеристик к частотным характеристикам. Проведено моделирование данной системы в среде «Matlab+Simulink», которая позволяет вводить нелинейности различного вида и описывать динамические процессы электрогидравлического привода, неподдающиеся линеаризации. Для анализа устойчивости исследуемой гидравлической системы управления при заданных значениях коэффициентов были получены логарифмические амплитудные фазовые частотные характеристики. Частотные характеристики позволяют анализировать структуры электрогидравлических систем на этапах проектирования, а также при эксплуатации существующих приводов, решать задачи синтеза путем подбора корректирующих звеньев.

Статья в формате PDF

0 KB

электрогидравлический привод

передаточная функция

амплитудно-фазовая частотная характеристика

1. Боровин Г.К., Костюк А.В. Математическое моделирование гидравлического привода с LS-управлением шагающей машины. Препринт № 54. – М.: Институт прикладной математики. им. М.В. Келдыша РАН, 2001.

2. Дьяконов В.П. MATLAB R2006/2007/2008 + Simulink 5/6/7. Основы применения. – 2-е изд., перераб. и доп. Библиотека профессионала. – М.: СОЛОН-Пресс, 2008. – 800 с.

3. Крымов Б.Г., Рабинович Л.В., Стеблецов В.Г. Исполнительные устройства системы управления летательными аппаратами. – М.: Машиностроение, 1987.

4. Навроцкий К.Л. Теория и проектирование гидро- и пневмоприводов. – М.: Машиностроение, 1991. – 384 с.

5. Ратушняк А.И., Каргу Д.Л. Исследование путей построения и обоснование новых схемных решений систем диагностирования и контроля динамических режимов работы приводов ракетных двигателей // Современные проблемы улучшения тактико-технических характеристик ракетно-космической техники, ее создания, испытаний и эксплуатации: труды Всероссийской научно-практической конференции. – СПб.: ВКА имени А.Ф. Можайского, 2013. – С. 115–121.

Несмотря на тенденцию широкого внедрения ЭВМ в область анализа и синтеза автоматических систем частотные методы исследования динамики проектируемых систем не утратили своего значения. Реализация их на ЭВМ дает возможность в короткий срок получить ценную информацию о проектируемой системе. По амплитудно-фазовым частотным характеристикам можно судить о таких качественных показателях, как запасы устойчивости по амплитуде и по фазе, резонансная частота и другие [2].

Основной задачей для экспериментального снятия частотных характеристик является математическое описание динамики автоматических систем управления в виде передаточных функций [1].

Широкое применение электрогидравлических приводов (ЭГП) ракет-носителей обусловлено высокой плотностью создаваемых усилий на единицу площади гидроусилителя.

В гидроприводе использованы распределители с пропорциональным управлением и гидроцилиндр.

При проектировании ЭГП оценка устойчивости, качества регулирования и коррекции динамических характеристик привода является важной задачей. Для выполнения этой задачи необходимо разработать математическую модель процессов, протекающих в приводе.

На рис. 1 приведена функциональная схема электрогидравлического привода.

В состав электрогидравлического привода ракеты-носителя входят: электромеханический преобразователь, гидроусилитель, золотник, силовой гидроцилиндр, формирователь тока управления, блок обратной связи. ЭГП является автоматической системой регулирования с отрицательной обратной связью.

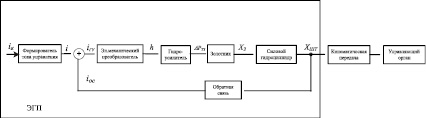
Рис. 1. Функциональная схема электрогидравлического привода

При составлении линейной модели ЭГП были приняты следующие предположения и допущения: коэффициенты расходов дросселей и рабочих окон золотника являются постоянными; перетечки рабочей жидкости через радиальные зазоры золотников и гидроцилиндров пренебрежимо малы; давление нагнетания слива постоянно; величины вязкости и модуля объёмной упругости не изменяются [3, 5].

Уравнение цепи управления электромагнита в электромеханическом преобразователе имеет следующий вид:

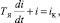(1)

где i – ток в ЭМП; TЯ – постоянная времени вихревых токов якоря ЭМП; iК – командный ток.

Уравнение в операторной форме и передаточная функция цепи управления электромагнита примут вид

(TЯs + 1)i = iК;

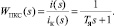(2)

Уравнение сигнала рассогласования представлено в следующем виде:

C_h = K_FI(i – i_OC) – K_CA_CΔP_ТЗ, (3)

где i_OC = K_OCX_ШТ – ток обратной связи; K_OC – коэффициент обратной связи; X_ШТ – перемещение штока привода; C_h – сигнал управления; h – величина смещения заслонки; K_FI – коэффициент передачи усилия ЭМП; K_C – коэффициент, учитывающий отношение диаметра торца сопла к диаметру сопла; A_C – эффективная площадь заслонки; ΔP_ТЗ– перепад давления на торцах золотника.

С другой стороны, динамика изменения перепада давления на торцах золотника описывается выражением

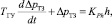(4)

где TГУ – постоянная времени гидроусилителя; KPh – коэффициент усиления по давлению.

После преобразования передаточная функция звена, определяющего зависимость перепада давления на торцах золотника от смещения заслонки, будет иметь вид

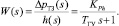(5)

Уравнение движения золотника имеет вид

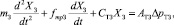(6)

где X_З – перемещение золотника; m_З – масса золотника; A_ТЗ, C_ТЗ, f_{mp З} – площадь торцов, жесткость пружин на торцах и коэффициент вязкого трения золотника.

Отсюда передаточная функция золотника будет иметь вид

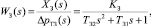(7)

где 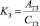– коэффициент передаточной функции золотника;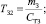 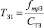– постоянные времени золотника.

Для структурной схемы узла управления, в состав которой входят ЭМП, гидроусилитель и золотник, из выражения (3) получим

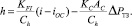(8)

Расход рабочей жидкости через силовой гидроцилиндр представлен в следующем виде:

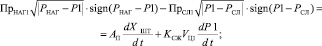
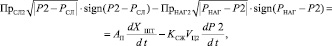
а уравнение движения штока с поршнем гидроцилиндра с массой mП

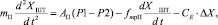
где X_ШТ – перемещение штока; P_НАГ, P_СЛ – давления нагнетания и слива; P1, P2 – давления в полостях гидроцилиндра; mП, AП – масса и площадь поршня гидроцилиндра; VЦ1,2 – объемы полостей гидроцилиндра; KСЖ – коэффициент, учитывающий сжимаемость рабочей жидкости; fmpП – коэффициент вязкого трения поршня; CE – эквивалентная жесткость рулевой проводки; ΔX – рассогласование между координатой штока и координатой массы качающейся части двигателя; ПРНАГ1,2, ПРСЛ1,2 – проводимости окон золотника; причем

ПРН1 = ПРС2 = KЗ(XЗ – XЗ0) при XЗ > XЗ0;

ПРН2 = ПРС1 = KЗ(–XЗ – XЗ0) при XЗ < –XЗ0,

KЗ – коэффициент расхода; XЗ0 – перекрытие золотника.

Из-за невозможности получения аналитического решения зависимости перепада давлений в полостях гидроцилиндра P1, P2 от перемещения золотника XЗ преобразуем уравнения для расхода рабочей жидкости через силовой гидроцилиндр путем линеаризации их левых частей. В результате получим

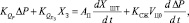(9)

где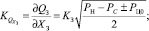

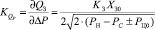– коэффициенты линеаризации; QЗ – расход через основной золотник; ΔP2 – P1 – перепад давления в полостях гидроцилиндра; VЦ0 – объем полости цилиндра при симметричном положении поршня; X30, PЦ0 – перемещение золотника и давление нагрузки в точке линеаризации.

После преобразований получим линеаризованное уравнение расхода через основной золотник в операторной форме

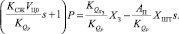
Из уравнения движения штока с поршнем гидроцилиндра передаточная функция давления в силовом гидроцилиндре будет иметь вид

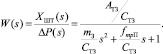
Структурная схема электрогидравлического привода, представленная на рис. 2, состоит из передаточных функций всех элементов, входящих в него.

Структурная схема электрогидравлического привода была смоделирована в среде «Matlab + Simulink» [4]. При этом имеется возможность ввода нелинейностей различного вида, которые позволяют описать процессы неподдающиеся линеаризации. В модели привода используются нелинейности, которые ограничивают выходную величину. Такие блоки имитируют ограничение перемещения заслонки и золотника, входящих в состав узла управления, а также ограничение перемещения штока силового гидроцилиндра.

Результаты моделирования

Важной динамической характеристикой систем автоматического управления являются частотные характеристики, достоинство которых состоит в том, что частотные характеристики позволяют просто выявлять влияние того или иного параметра на динамические свойства системы (устойчивость, переходный процесс и т.д.). Для анализа устойчивости исследуемой гидравлической системы управления при заданных значениях коэффициентов в дифференциальных уравнениях были получены логарифмические амплитудные фазовые частотные характеристики (ЛАФЧХ) разомкнутой цепи. ЛАЧХ и ЛФЧХ для электрогидравлического привода представлены на рис. 3.

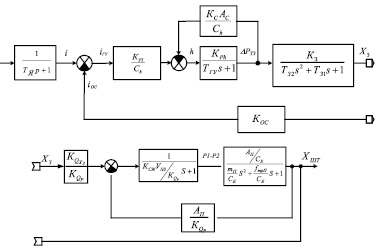
Рис. 2. Структурная схема электрогидравлического привода

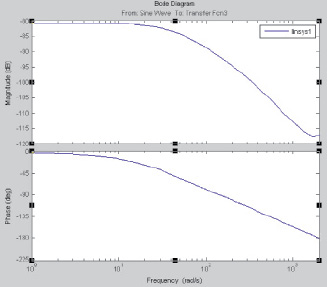
Рис. 3. Логарифмические амплитудные и фазовые частотные характеристики разомкнутой цепи электрогидравлического привода

Запасы по частоте и амплитуде должны быть не менее определенных значений. Рекомендуемые запасы по амплитуде – 6–8 дБ, по фазе – 40°. Для данного электрогидравлического привода запас по амплитуде составляет 115 дБ, запас по фазе 56°, что является вполне достаточным для устойчивого функционирования привода. Проведенный анализ показывает, что данный электрогидравлический привод устойчив.

Заключение

Проектирование систем управления с помощью амплитудно-фазовых частотных характеристик дает возможность анализировать структуры и влияние параметров объекта и отдельных его частей, решать задачи синтеза регулятора путем подбора корректирующих звеньев, выполнять идентификацию по экспериментально снятым частотным характеристикам и решать другие задачи.

Библиографическая ссылка