Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Киборт И.Д. 1

---

1 Ухтинский государственный технический университет

Данная статья представляет результаты анализа наиболее значимых параметров работы системы утилизации тепловой энергии удаляемого воздуха систем кондиционирования и вентиляции на основе воздушного теплового насоса, полученных путем проведения имитационного моделирования. Результатами моделирования является массив параметров работы системы утилизации для широкого спектра исходных данных. В результате систематизации полученного массива был сформирован ряд ключевых зависимостей. В частности, приводятся зависимости изменения площади теплообменной поверхности теплообменных аппаратов системы утилизации от изменения ключевых температур рабочего тела и воздушной среды. Приведено последовательное сравнение влияния изменения температур хладагента в узловых точках парокомпрессионного цикла на величину коэффициента преобразования энергии. Выявлены наиболее значимые характеристики, динамика изменения которых оказывает наиболее существенное влияние на работу системы утилизации. Для каждой рассмотренной зависимости представлена аппроксимирующая кривая и соответствующая характерная функция.

Статья в формате PDF

0 KB

утилизация теплоты удаляемого воздуха

воздушный тепловой насос

моделирование

энергоэффективность

1. Богословский В.Н., Поз М.Я. Теплофизика аппаратов утилизации тепла систем отопления, вентиляции и кондиционирования воздуха. – М.: Стройиздат, 1983. – 319 с.

2. Лебедев В.Ф., Чурмак Г.Д., Аверин Ю.Д. Холодильная техника. – М.: Агропромиздат, 1986. – 335 с.

3. Уляшева В.М. Энергосберегающие мероприятия на компрессорных станциях / В.М. Уляшева, И.Д. Киборт // «СОК» Ежемесячный специализированный журнал. – 2013. – № 2. – С. 64–69.

4. Рейй Д., Макмайл Д. Тепловые насосы. – М.: Энергоиздат, 1982. – 224 с.

5. Розенфельд Л.М., Ткачев А.Г. Холодильные машины и аппараты. – М.: Госторгиздат, 1960. – 656 с.

Современные способы утилизации тепловой энергии в системах вентиляции и кондиционирования являются актуальной темой научных изысканий, содержащих исчерпывающий аналитический базис. Он позволяет, оперируя накопленным опытом, производить более оперативный и точный подбор оборудования в рамках выбранной проектом методики. Во многом накопление данного базиса было обеспечено силами математического и виртуального моделирование [1]. В случае, когда речь идет о непопулярных или новых способах утилизации тепловой энергии, именно математическое и виртуальное моделирования является самым очевидным и простым в реализации методом накопления аналитической информации, пригодной для дальнейшей обработки [2].

Рассмотрим особенности анализа результатов моделирования работы системы утилизации тепловой энергии на основе воздушного теплового насоса (ТН). Исследование вопроса моделирования системы рекуперации теплоты удаляемого воздуха на основе ТН показало, что возможное число вариантов исполнения системы может быть более 136000. В таком случае возможность визуального восприятия подобного массива данных является более рациональным способом анализа данных [3]. В число основных проблем составления удобного визуального массива входит трудность рациональной организации данных. Решением подобной задачи является оптимизация массива путем выделения наиболее существенных переменных, оказывающих непосредственное влияние на показатели работы рассматриваемой системы утилизации.

Основу предлагаемой виртуальной модели составляют расчетные алгоритмы, написанные на языках Visual Basic и PHP. Обработка выходных данных выполнялась при помощи программных продуктов, таких как Microsoft Excel и MathWorks – MATLAB.

Рассмотрим результаты моделирования работы воздухоохладителя при расходе воздуха L = const = 1000 м3/ч, скорости течения хладагента w = const = 1 м/с с целью определения тенденций изменения площади теплообменной поверхности. В качестве хладагента принят R22.

Для всех рассматриваемых вариантов введем следующие обозначения:

F – площадь поверхности теплообмена, м2;

t1 – начальная температура воздуха, °С;

t2 – конечная температура воздуха, °С. t2 = const;

t3 – начальная температура хладагента, °С;

t4 – конечная температура хладагента, °С.

Ситуация № 1.1: значения t3, t4 = const, значение t1 возрастает, тем самым увеличивая величину теплового потока. Для рассматриваемой системы изменение величины F описывается аппроксимирующей функцией (1), выведенной методом наименьших квадратов:

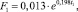м2. (1)

Ситуация № 1.2: t1, t2, t4 = const, значение t3 убывает, тем самым увеличивая разность температур хладагента в процессе испарения. В данном случае имеем зависимость, характеризуемую аппроксимирующей функцией

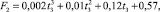м2. (2)

Ситуация № 1.3: t2, t4 = const, значение t1 возрастает, тем самым увеличивая величину теплового потока, значение t3 убывает, при этом увеличивая разность температур хладагента в процессе испарения. Характерное поведение графика представлено на рис. 1.

Ситуация № 1.4: t1, t2, t3 = const, значение t4 возрастает. Ситуация аналогична ситуации № 1.2, за исключением изменяемого параметра. Характерное поведение графика представлено на рис. 2.

В математическом виде данную зависимость можно охарактеризовать аппроксимирующей функцией

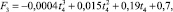м2. (3)

Уравнения (2) и (3) имеют вид полинома третьего порядка, коэффициенты которых имеют сопоставимые значения, что еще раз подтверждает идентичность тенденций ситуаций 1.2 и 1.4.

Систематизация полученных зависимостей представлена в табл. 1.

Далее рассмотрим зависимости значения площади теплообменной поверхности нагревателя от температур наружного воздуха и сжатого хладагента. Обозначения принимаются те же, что и для ситуации с воздухоохладителем.

Ситуация № 2.1: t1, t2, t4 = const, значение t3 возрастает. Результаты расчета представлены на рис. 3. В итоге рост значения Δt3-4 обеспечивает снижение требуемой площади теплообменной поверхности согласно аппроксимирующей функции

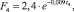м2. (4)

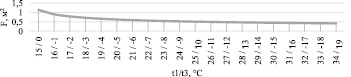
Рис. 1. Функция изменения значения площади теплообменной поверхности для ситуации № 1.3

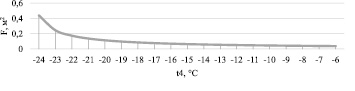
Рис. 2. Функция изменения значения площади теплообменной поверхности для ситуации № 1.4

Таблица 1

Сводные данные анализа результатов моделирования работы воздухоохладителя

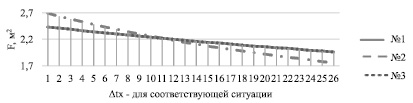
Рис. 3. Функции изменения значения F для ситуаций № 2.1, 2.2, 2.3

Ситуация № 2.2: t1, t2 = const, значения t3, t4 возрастают, Δt3-4 = 10 °С = const. Результаты расчета представлены на рис. 3. Функция изменения необходимой площади имеет более крутой характер, нежели функция, характерная для ситуации № 2.1. Для ситуации № 2.2 значение площади можно определить при помощи аппроксимирующей функции

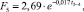м2. (5)

Ситуация № 2.3: t1, t2, t3 = const, значение t4 возрастает. Результаты расчета представлены на рис. 3.

Ситуация № 2.4: t1, t3, t4 = const, значение t2 убывает. Результаты расчета представлены на рис. 4. Зависимость значения F от t2 в данной ситуации описывается аппроксимирующей функцией

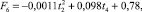м2. (6)

Ситуация № 2.5: t3, t4 = const, значения t1, t2 возрастают, Δt1-2 = 20 °С = const. Результаты расчета представлены на рис. 4. Значение F в данной ситуации описывается аппроксимирующей функцией

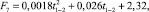м2. (7)

Ситуация № 2.6: t2, t3, t4 = const, значение t1 убывает. Результаты расчета представлены на рис. 4. В данной ситуации значение F определяется при помощи аппроксимирующей функции

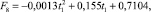м2. (8)

Систематизация полученных зависимостей представлена в табл. 2.

Рис. 4. Функции изменения значения F для ситуаций № 2.4, 2.5, 2.6

Таблица 2

Сводные данные анализа результатов моделирования работы воздухонагревателя

Далее рассмотрим зависимости работы цикла ХМ от ключевых температур.

Таким образом, ключевыми температурами являются:

t2 – температура хладагента после испарителя ХМ, °С.

t3 – температура хладагента после компрессора ХМ, °С.

t4 – температура хладагента после конденсатора ХМ, °С.

Аналогично анализу результатов расчета площади теплообменной поверхности проведем расчет значения КПЭ для различных ситуаций.

Ситуация № 3.1: t2, t4 = const, значение t3 возрастает. Результаты расчета представлены на рис. 5. В данной ситуации значение КПЭ определяется при помощи аппроксимирующей функции

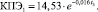(9)

Ситуация № 3.2: t3, t4 = const, значение t2 убывает. Результаты расчета представлены на рис. 5. Зависимость КПЭ от t2 в данной ситуации описывается аппроксимирующей функцией

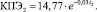(10)

Ситуация № 3.3: t2, t3 = const, значение t4 возрастает. Результаты расчета представлены на рис. 5. Для ситуации № 3 характерно линейное соотношение значений КПЭ и t4, что выражается при помощи аппроксимирующей функции

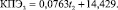(11)

Ситуация № 3.4: t2 = const, значения t3, t4 возрастают, Δt3-4 = 30 °С = const. Результаты расчета представлены на рис. 5.

Систематизация полученных зависимостей представлена в табл. 3.

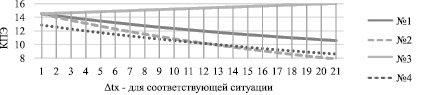
Рис. 5. Графики изменения значения КПЭ для различных ситуаций

Таблица 3

Сводные данные анализа результатов моделирования работы цикла теплового насоса

В общем итоге анализ результатов позволил сформулировать следующие выводы.

В системе отношений показателей работы воздухоохладителя ключевое значение на конечную эффективность процесса утилизации тепловой энергии при помощи ХМ оказывают изменения значений начальной температуры воздуха (t1) и начальной температуры (t3). В условиях работы рекуператора значение температуры удаляемого воздуха после рекуператора целесообразно принять равным 2 °С с целью профилактики обмерзания конденсатора [4].

В системе отношений показателей работы воздухонагревателя минимальная величина площади теплообменной поверхности воздухонагревателя достижима при максимальной разнице между начальными температурами воздуха и хладагента (Δt1-3) и при минимальных значениях разницы температур до и после нагревателя (Δt1-2) [5]. Есть два пути достижения заданного условия:

1. Увеличение температуры хладагента после компрессора холодильной машины (ХМ).

2. Внедрение нагревателя наружного воздуха (испарителя ХМ) в качестве первой ступени обработки воздуха до основного подогревателя.

В системе отношений показателей работы холодильного цикла стимулом к росту КПЭ является увеличение значения температуры хладагента после конденсатора, а также снижение разницы температур хладагента до и после компрессора.

Рассматривая утилизатор как систему, необходимо вводить понятие общей эффективности, где в противовес количеству утилизированной тепловой энергии ставится потребляемая электроэнергия на привод компрессора и вентилятора.

В данном случае особый интерес представляет количество энергии, необходимое на преодоление сопротивлений теплообменных аппаратов. При этом значение общего КПЭ будет определяться по формуле, выведенной аналитически.

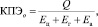(12)

где Q – полная теплопроизводительность СУ, кВт; Eц – количество электрической энергии, необходимой на обеспечение работы цикла, кВт; Eг – количество электрической энергии, необходимой на преодоление гидравлических сопротивлений теплообменных аппаратов (ГС), определяемое по формуле (13), кВт; Eа – количество электрической энергии, необходимой на преодоление аэродинамических сопротивлений теплообменных аппаратов (АС), определяемое по формуле (14), кВт.

Величина Eа не имеет непосредственного влияния на параметры самой ХМ. Однако учитывая, что дополнительное сопротивление будет оказывать нагрузку на элементы конечной системы, то возросшее потребление электроэнергии на привод вентилятора необходимо учитывать при расчете КПЭ.

Численный коэффициент 20,482 – математически полученное соотношение среднего КПД привода компрессора, электродвигателя и коэффициента определения значения гидравлического сопротивления теплообменного аппарата. Значение 20,482 характерно для испарителей, значение 4,168 характерно для конденсаторов [4].

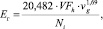кВт, (13)

где VFh – объемный расход хладагента, м3/ч; vg – скорость движения хладагента, м/с; Ni – индикаторный КПД компрессора ХМ;

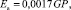кВт, (14)

где G – расход приточного воздуха, м3/с; P – аэродинамическое сопротивление теплообменного аппарата, Па.

Библиографическая ссылка