В настоящее время актуальной проблемой при решении задач эффективной организации движения является возможность прогнозирования распределения транспортных потоков по сети в режиме реального времени. Имея аппарат для определения в режиме on-line параметров распределения транспортных средств по улично-дорожной сети, возможно рассчитывать задержки транспортных средств при различной схеме организации движения на подходах к перекрестку, определять целесообразность введения или отмены светофорного регулирования при той или иной схеме организации движения, определять оптимальные параметры светофорного регулирования с краткосрочной задержкой реагирования на изменения в интенсивности движения транспортных средств по различным направлениям, выбирать оптимальные маршруты для отдельных транспортных средств.
Разработанная авторами мезоскопическая модель TIMeR_Mod дает возможность решать как задачи, требующие выдачи результатов в режиме реального времени, что особенно важно для Интеллектуальных транспортных систем, так как позволит динамично информировать участников дорожного движения, так и прогнозные задачи.
Точность выдаваемых результатов зависит от того, насколько точно предсказаны исходные данные для модели. При применении с этой целью фильтра Кальмана на каждом этапе прогнозируемые данные корректируются с помощью данных, полученных с помощью непосредственных измерений. Это позволяет увеличить эффективность принятия решений по организации движения.
Структура матриц ASTREETS и BINTERSECTION, содержащих информацию о распределении транспортных потоков по сети
Исходными данными для решения различных транспортных задач с помощью модели TIMeR_Mod является текущая схема организации движения на улично-дорожной сети и параметры распределения транспортных потоков по полосам. Ключевой гипотезой модели является предположение, что временные интервалы в потоках распределены по обобщенному закону Эрланга [5]. Поэтому для модели TIMeR_Mod описать транспортный поток – значит указать для него параметры обобщенного закона Эрланга. Все необходимые данные для модели содержатся в матрицах ASTREETS и BINTERSECTION. Ниже приведена их структура.
I. ASTREETS = (S1 S2 S3 S4 Contr Pr Len Col AL AS AR λА1 kA1 ... BL BS BR λВ1 kB1 ...)
1) № – номер строки матрицы ASTREETS соответствует номеру дуги графа, соединяющей узловые точки I и II; количество строк соответствует количеству дуг графа;
2) S1 и S2 – пересекающиеся магистрали, образующие вершину I графа;
3) S3 и S4 – пересекающиеся магистрали, образующие вершину II графа;
4) Contr – тип узловой точки (регулируемый или нерегулируемый перекресток);
5) Pr – наличие приоритета (главная или второстепенная магистраль);
6) Len – длина дуги между узловыми точками;
7) Col – количество потоков на дуге;
8) AL – допустимость поворота налево из направления А в вершине II;
9) AS – допустимость движения прямо из направления А в вершине II;
10) AR – допустимость поворота направо из направления А в вершине II;
11) λА1, λА2 и т.д. – параметры λ в направлении А;
12) kA1, kA2 и т.д. – параметры k в направлении А;
13) BL – допустимость поворота налево из направления В в вершине I;
14) BS – допустимость движения прямо из направления В в вершине I;
15) BR – допустимость поворота налево из направления В в вершине I;
16) λВ1, λВ2 и т.д. – параметры λ в направлении В;
17) kB1, kB2 и т.д. – параметры k в направлении В.
II. BINTERSECTION = (S1 S2 λCline1 kCline1 ... λDline1 kDline1)
1) № строки совпадает с номером дуги графа, соединяющей узловые точки I и II в матрице ASTREETS;
2) S1 и S2 – пересекающиеся магистрали, образующие вершину I графа;
3) λCline1, λCline2 и т.д. – параметры λ потоков, входящих в вершину I в направлении С магистрали, пересекающей данную дугу графа в узловой точке I;
4) kCline1, kCline2 и т.д. – параметры k потоков, входящих в вершину I в направлении С магистрали, пересекающей данную дугу графа в узловой точке I;
5) λDline1, λDline2 и т.д. – параметры λ потоков, входящих в вершину I в направлении D магистрали, пересекающей данную дугу графа в узловой точке I;
6) kDline2 и т.д. – параметры k потоков, входящих в вершину I в направлении D магистрали, пересекающей данную дугу графа в узловой точке I.
Количество строк матриц равно количеству дуг графа. Параметры λ и k для каждого из направлений движения формируются в порядке следования потоков справа налево (от обочины к середине дороги). Матрица ASTREETS уже содержит информацию обо всех потоках сети и организации движения на перекрестках. Матрица BINTERSECTION введена для удобства получения необходимой для расчетов информации и удобства идентификации перекрестка при его моделировании.
Метод прогнозирования и корректировки параметров распределения Эрланга
Для прогнозирования матрицы корреспонденций, интенсивности движения между отдельными пунктами «источник – сток» используют наблюдения в предыдущие промежутки времени. При этом возможны и ошибки измерений, проведенных с помощью разнообразных измерительных приборов, и ошибки, вызванные упрощениями при составлении математической модели. И те, и другие ошибки неизбежны. Фильтр Кальмана [3] позволяет оптимизировать прогнозы за счет минимизации квадрата отклонения ошибок.
Для модели TIMeR_Mod необходимо с помощью датчиков видеонаблюдения измерять временные интервалы между подряд идущими автомобилями в потоке по отдельной полосе движения. С помощью этих измерений получают следующие статистические точечные оценки параметров:
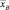– выборочная средняя случайной величины T – интервала между следующими подряд по одной полосе автомобилями;
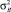– выборочная дисперсия случайной величины.
Затем с их помощью рассчитывают параметры обобщенного закона Эрланга, необходимые для проведения всех остальных расчетов и решения транспортных задач. Подробно метод определения указанных параметров можно посмотреть в работе [2]. В настоящий момент важно, что параметр Эрланга λ0 определяется следующим образом:
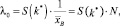(1)
где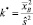 
; N – интенсивность движения по данной полосе. Функция S(k*) для различных значений параметра k = [k*] + 1 различна.
Остальные параметры обобщенного закона Эрланга:
λi = x i+1 •λ0,
i ∈ {1, ..., k – 1}; k = [k*] + 1 – целое число, большее k*.
При изменении интенсивности параметр распределения Эрланга λ0 меняется. Если известен закон изменения интенсивности, есть возможность предсказать значение параметра λ0, и, соответственно, решать прогнозные задачи о матрице корреспонденций, эффективности организации движения и т.п.
Пусть для изменения интенсивности построена регрессионная модель:
N(t) = N0 + nt.
Или, разбив всю временную ось на отдельные промежутки:
Nk+1 = Nk + n•Δt.
Обозначим:
(λ0)k – значение параметра в k-й промежуток времени.
Тогда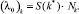 
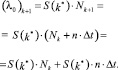(2)
Так как при составлении регрессионной модели для интенсивности, естественно, возникли случайные ошибки, следует преобразовать формулу (2) следующим образом:
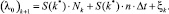(3)
При этом рассчитанное по данным видеорегистратора значение (Λ0)k отличается от его истинного значения (λ0)k:
(λ0)k = (λ0)k + ηk. (4)
Ошибка модели ξk и ошибка сенсора ηk – случайные величины. И их законы распределения не зависят от времени (от номера итерации k). Средние значения M(ξk) = 0, M(ξk) = 0.
Предполагается, что все случайные ошибки независимы друг от друга.
Необходимо знать дисперсии случайных величин ξ и η. Точечную оценку дисперсии случайной величины ξ можно вычислить off-line по непосредственным измерениям, выразив ее наблюдаемые значения из модели (3) и применив соответствующую формулу математической статистики [1].
Определим теперь способ получения оценки дисперсии случайной величины η.
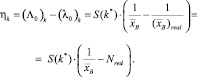
Тогда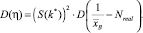 
Наша задача – найти наилучшее приближение к истинному значению параметра λ0 на (k + 1)-м шаге (обозначим (λ0)k+1). Для этого требуется выбрать нечто среднее между показанием датчиков и предсказанием того, что ожидается от них увидеть. Если показанию датчика присвоить вес K, тогда на предсказанное значение останется вес (1 – K):
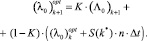(5)
Число K – это коэффициент Кальмана. Он зависит от шага итерации. В общем случае, чтобы найти точное значение коэффициента Кальмана K, нужно минимизировать ошибку:
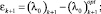
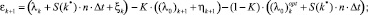
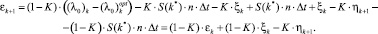
Итак, выражение для ошибки:
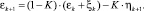(6)
Математическое ожидание квадрата ошибки:
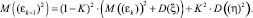(7)
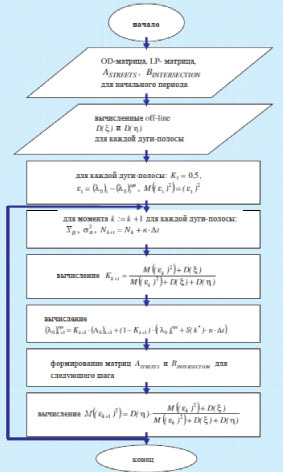
Алгоритм формирования матриц ASTREETS и BINTERSECTION при автоматизированном решении задач эффективной организации движения транспортных средств
Если найти производную по переменной K и приравнять ее к нулю, то
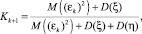(8)
где Kk+1 – коэффициент Кальмана на шаге (k + 1).
Подставим (8) в (7), получим
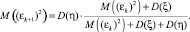(9)
Таким образом, мы прогнозируем значение параметров распределения Эрланга, используя данные предыдущих наблюдений и прогноз интенсивности на следующий по времени шаг. Алгоритм формирования матриц ASTREETS и BINTERSECTION при автоматизированном решении задач эффективной организации движения транспортных средств представлен на рисунке.
Параметры Эрланга – основной элемент при расчетах функции транспортных затрат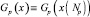 
по маршрутам сети с помощью модели TIMeR_Mod. То есть получен аппарат для прогнозирования изменений в затратах по маршрутам. А следовательно, можем корректировать матрицу корреспонденций на следующий по времени шаг с учетом текущих изменений в распределении транспортных потоков.
Заключение
Задача динамического отслеживания изменений в параметрах транспортных потоков стала очень актуальной в связи с повсеместным внедрением Интеллектуальных транспортных систем. Получение адекватного математического аппарата, позволяющего в режиме реального времени динамично обрабатывать и преобразовывать в показатели эффективности параметры мониторинга транспортных потоков, является актуальной задачей. Для увеличения точности прогнозируемых параметров применяли фильтрацию Кальмана, например, Xuesong Zhou, Hani S. Mahmassani [6]; Nanne J. van der Zipp и Rudi Hamerslag [4]. Фильтр Калмана – это мощнейший инструмент фильтрации данных. Основной его принцип состоит в том, что при фильтрации используется информация о физике самого явления. Из всех линейных фильтров Калмановский фильтр самый лучший в том смысле, что средний квадрат ошибки фильтра минимален. А уровень оперативности и эффективности управленческих решений напрямую зависит от точности прогнозируемых параметров управления транспортными потоками.
Работа выполнена при поддержке РФФИ и администрации Краснодарского края, проект р-юг-а -16-48-230720.
Библиографическая ссылка
Данович Л.М., Наумова Н.А. ПРОГНОЗИРОВАНИЕ ИСХОДНЫХ ДАННЫХ В ДИНАМИЧЕСКОМ РЕЖИМЕ ДЛЯ МОДЕЛИ РАСПРЕДЕЛЕНИЯ ТРАНСПОРТНЫХ ПОТОКОВ ПО СЕТИ // Фундаментальные исследования. – 2016. – № 9-2. – С. 238-242;URL: https://fundamental-research.ru/ru/article/view?id=40727 (дата обращения: 20.04.2024).