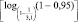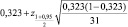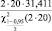Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Петросян Г.С. 1 Титов В.А. 1

---

1 ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова»

Настоящая статья посвящена анализу плавающих дефектов, что является актуальной задачей в области тестирования и обеспечения качества ПО. Дано определение плавающих дефектов, рассмотрены основные особенности и риски, связанные с управлением данными дефектами. В?частности, описана классификация плавающих дефектов согласно инженерному стандарту IEEE?1044. В?работе предложены две математические модели анализа плавающих дефектов. При построении данных моделей был использован аппарат теории вероятностей и математической статистики. Приведены конечные формулы для точечных и интервальных оценок следующих показателей: вероятность проявления дефекта, среднее и худшее число попыток до воспроизведения дефекта, среднее и худшее время до воспроизведения дефекта. На различных примерах из банковской сферы показано применение предложенных зависимостей. Представленные модели реализованы с использованием языка программирования R. Делается вывод о том, что предлагаемые модели могут облегчить работу тестировщиков, разработчиков и руководителей IT-проектов. Результаты статьи могут использоваться как в учебном процессе, так и в?практической деятельности IT-компаний.

Статья в формате PDF

0 KB

тестирование ПО

управление дефектами

плавающие дефекты

вероятность проявления дефекта

статистическое оценивание

язык программирования R

1. Вентцель Е.С., Овчаров Л.А. Теория вероятностей и ее инженерные приложения. – М.: Высшая Школа, 2000.

2. Смирнов Н.В., Дунин-Барковский И.В. Курс Теории Вероятностей и математической статистики для технических приложений. – М.: Наука, 1969.

3. [IEEE1044] IEEE Standard Classification for Software Anomalies. – URL: http://www.ctestlabs.org/neoacm/1044_2009.pdf.

4. Ross, Sheldon M. (2009). Introduction to probability and statistics for engineers and scientists (4th ed.). Associated Press, – P. 267.

5. The R Manuals [Электронный ресурс]. – Режим доступа: https://cran.r-project.org/manuals.html (дата обращения: 10.06.2016)

В условиях интенсивного развития информационных технологий и усложнения программных комплексов в конце XX столетия (80–90-е гг.) сформировалась отдельная ветвь компьютерных наук – тестирование ПО. Одна из задач в тестировании ПО – это нахождение дефектов, то есть несоответствий реального и ожидаемого поведения ПО.

После того, как дефект найден, специалист по тестированию должен составить для него грамотное и однозначное описание. Указанный в отчёте об ошибке сценарий должен приводить к проявлению данной ошибки в 100 % случаев.

Существует класс дефектов, для которых данная задача не является тривиальной. Пожалуй, каждый специалист по тестированию сталкивался с проблемой воспроизводимости: ошибка возникает, к примеру, 4 раза из 10. Такие ошибки принято называть «фантомными» или «плавающими».

Плавающим называется дефект, чёткие шаги для воспроизведения которого не очевидны либо отсутствуют.

Разработчик, который должен исправить тот или иной плавающий дефект, заинтересован в максимально подробном его описании. Так, например, фраза «Ошибка воспроизводится не всегда» представляет для разработчика меньшую ценность, чем «Для воспроизведения ошибки потребуется в среднем 5 попыток». В случае, когда описание дефекта является расплывчатым, существует риск того, что ответственный за исправление переведёт данный дефект в статус «Невозможно воспроизвести» (Cannot reproduce) или, что хуже, отложит исправление проблемы «на потом».

Как следствие, необходимы специальные методы составления правильных отчётов о таких ошибках. В силу стохастической природы рассматриваемого нами класса дефектов, разработка данных методов невозможна без использования аппарата теории вероятностей и математической статистики.

В современной отечественной и зарубежной литературе по информационным технологиям и тестированию ПО слабо отражены принципы работы с плавающими дефектами, в частности, использование вероятностных методов в анализе подобных дефектов.

Целью данной работы является построение двух математических моделей анализа плавающих дефектов в прикладном программном обеспечении.

В стандарте IEEE 1044 (Standart Classification for Software Anomalies) наряду с такими атрибутами дефекта, как Критичность (Severity) и Приоритетность (Priority), можно видеть ещё один не менее важный атрибут – Вероятность (Probability) проявления данного дефекта [3]/

В документе также указаны возможные значения данного атрибута:

- Высокая (High) – значение вероятности более 70 %.

- Средняя (Medium) – значение вероятности находится между 40 и 70 %.

- Низкая (Low) – Значение вероятности менее 40 %.

Однако в рассматриваемом инженерном стандарте не описываются способы оценки данной вероятности.

Перейдём к рассмотрению первой из двух моделей – к модели воспроизведения ошибки, основанной на cхеме испытаний Бернулли. Основной задачей в рамках данной модели является оценка вероятности проявления дефекта для последующего указания в отчёте о данном дефекте.

Напомним, что схемой испытаний Бернулли принято называть серию последовательных испытаний, в которой любое испытание имеет только 2 исхода (например «дефект» и «отсутствие дефекта») и вероятности этих исходов не зависят от результатов предыдущих испытаний [1].

Дальнейшие расчёты будем производить в рамках следующего примера:

Рассмотрим тестирование системы интернет-банкинга. Иногда при попытке открыть web-форму для открытия депозита появляется сообщение об ошибке.

Попробуем воспроизвести дефект до 10-го его проявления.

Занесём результаты эксперимента в табл. 1, обозначив возникновение дефекта как «Fail» и его отсутствие как «?»:

Таблица 1

Статистика проявления дефекта в рамках примера с интернет-банкингом

Назовём эмпирической частотой проявления дефекта отношение числа испытаний, в котором дефект проявился (d) к общему кол-ву испытаний (n)

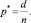(1)

Отсюда

d = 10 – число испытаний, в которых дефект проявился;

n = 31 – общее количество испытаний;

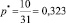 – эмпирическая частота проявления дефекта.

Доказано, что эмпирическая часто-
та p* является несмещенной, состоятельной и эффективной оценкой вероятности дефекта [2].

Очевидно, что при последующем повторении эксперимента, который заключается в попытке воспроизвести дефект до 10-го его проявления, мы будем наблюдать другое значение p*. Частота ошибки скорее всего будет отличаться от 0,323, даже если провести ровно 31 испытание.

Чтобы устранить этот недостаток, рассматривается задача построения доверительного интервала для вероятности дефекта.

В рамках схемы Бернулли доверительный интервал для вероятности имеет следующий вид [1]:

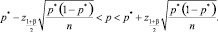(2)

Обозначения:

zγ – квантиль стандартного нормального распределения уровня γ;

β – доверительная вероятность;

p* – заранее рассчитанная эмпирическая частота дефекта;

n – число испытаний, на базе которых построена оценка p*.

Продемонстрируем использование формулы (2) при p* = 0,323; n = 31 и β = 0,95:

Для расчёта квантиля стандартного нормального распределения можно воспользоваться специальными таблицами или, что проще, функцией «qnorm()» в R.

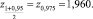
Таким образом, получим, что истинное значение вероятности p находится внутри интервала (0,158; 0,487).

Возможна и другая запись полученного результата: p = 0,323 ± 0,165.

Следует также отметить, что доверительный интервал расширяется при уменьшении n. Отсюда следует, что при небольшом количестве испытаний расчёт доверительного интервала не имеет практической значимости.

Таким образом, приведены конечные формулы для точечной и для интервальной оценок вероятности проявления
дефекта.

В рамках того же примера несложно рассчитать среднее количество попыток, которое было предпринято для того, чтобы наблюдать дефект. Данная величина может быть рассчитана как простая средняя арифметическая (табл. 2):

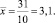
Вычислим теперь число попыток воспроизвести дефект, которое не будет превышено с заданной наперёд вероятностью α.

Доказано [1], что такое число попыток может быть найдено по следующей формуле:

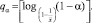(3)

В данной формуле:

α – заданная вероятность;

[y] – целая часть числа y.

Вернёмся к примеру с интернет-банком.

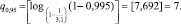
Таблица 2

Расчёт среднего количества попыток для воспроизведения дефекта в примере с интернет-банкингом

Таким образом, с вероятностью 95 % для воспроизведения дефекта понадобится не более 7 попыток.

Итак, теперь в отчёт об ошибке в интернет-банке может добавиться следующая информация:

«Вероятность дефекта ≈ 32,3 ± 16,5 % (низкая).

Среднее количество попыток для воспроизведения дефекта – 3,1.

С вероятностью 95 % для воспроизведения дефекта понадобится не более 7 попыток».

Не стоит забывать и о другой информации, которая поможет воспроизвести и локализовать дефект: логи, HTTP-запросы, и т.д. Подобные уточнения являются необходимым условием любого грамотного отчёта о плавающей ошибке.

Полученные результаты также могут быть использованы для того, чтобы убедить руководителя проекта по разработке интернет-банка в необходимости исправления дефекта:

«Ожидается, что в течение следующего месяца 15 000 пользователей попытаются произвести открытие депозита онлайн, при этом средний размер одного депозита составит 600 руб. В этих условиях наиболее вероятные потери от дефекта будут равны 2 907 000 ± 1 485 000 руб.».

Данные цифры были рассчитаны исходя из вероятности дефекта:

2 907 000 = 15 000?600?0,323;

1 485 000 = 15 000?600?0,165.

Рассмотрим недостатки данной модели.

Описанная выше модель основывается на двух предположениях, которые могут не выполняться в реальных условиях:

- Считается, что каждое последующее испытание не зависит от исходов предыдущих.

- Считается, что испытания независимы от прочих факторов (например, нагрузки на систему).

Теперь перейдем к рассмотрению простейшей модели времени до воспроизведения дефекта. В некоторых случаях такие показатели, как «вероятность дефекта» и «среднее число попыток» оказываются неприменимыми.

В качестве примера такой ситуации рассмотрим автоматизированную систему «Оповещения», которая отправляет клиентам банка SMS-сообщения об операциях по счетам и картам. Пусть по факту снятия средств в банкомате клиент получает необходимое оповещение, а спустя некоторый промежуток времени происходит ошибочная отправка дублирующего SMS. Причём этот промежуток времени иногда может составлять 8 мин, а иногда – 2 часа.

Данный дефект также можно отнести к классу плавающих.

В связи с этим разумно ввести такую характеристику, как «среднее время до воспроизведения дефекта».

Для моделирования времени будем использовать экспоненциальное распределение вероятностей.

В рамках примера с самопроизвольным переходом сделаем 20 попыток воспроизвести дефект (табл. 3):

Таблица 3

Статистика проявления дефекта в рамках примера с системой «Оповещения»

Тогда

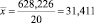 – среднее время до проявления дефекта.

Время, которое при попытке воспроизвести дефект не будет превышено с заданной наперёд вероятностью α, может быть вычислено как квантиль экспоненциального распределения уровня α [1]:

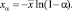(4)

Так, например:

x0,95 = –31,411?ln(1 – 0,95) = 94,100.

Для среднего значения времени до воспроизведения дефекта также можно построить доверительный интервал [4]:

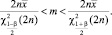(5)

Здесь 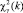 – это квантиль распределения хи-квадрата с k степенями свободы уровня γ; β – доверительная вероятность;  – заранее рассчитанное среднее значение; n – число испытаний, на базе которых рассчитано среднее значение ; m – «истинное значение среднего времени».

Воспользуемся формулой (5):

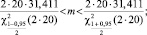
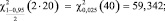
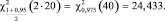
Итого,

21,173 < m < 51,424.

Перейдём к подведению итогов. В отчёт о рассматриваемой ошибке можно добавить следующую информацию:

«Ожидаемое время до отправки дублирующего сообщения ≈ 21,173 мин – 51,424 мин.

С вероятностью 95 % время до ошибочной отправки SMS не превысит 94,100 мин»

Рассмотрим недостатки второй модели. Данная модель также базируется на предположении о том, что испытания не зависят от прочих факторов (например, нагрузки на систему).

Отметим также, что время до воспроизведения дефекта может быть более точно смоделировано с помощью гамма-распределения. Рассмотрение данного метода выходит за рамки настоящей статьи в силу трудоёмкости расчётов, связанных с оценкой параметров гамма-распределения.

Таблица 4

Стандартные функции R

Таблица 5

Использование стандартных функций R

Для расчётов целесообразно воспользоваться статистическим пакетом R [5]. В табл. 4 приведены некоторые стандартные функции R.

В табл. 5 продемонстрируем использование функций R для решения наших задач (табл. 5).

В заключение необходимо упомянуть о риске ложного отчёта о плавающем дефекте. Перед тем как утверждать, что тот или иной дефект является плавающим, специалист по тестированию обязан потратить время и попытаться найти условия, при которых дефект возникает постоянно.

Стоит иметь в виду некоторые стандартные ситуации проявления плавающих ошибок: интернет работает с перебоями или блокирует определённые порты, определённый функционал также может блокировать антивирус и т.д.

Таким образом, рассмотрены два математических метода, которые удобно использовать для анализа некоторых плавающих дефектов.

Информация, полученная при помощи данных инструментов, несомненно, является необходимой как для лица, ответственного за исправление дефекта, так и для руководителя IT-проекта, в рамках которого возник тот или иной дефект.

Библиографическая ссылка