Описание функционирования экономических систем (ЭС) требует учета множества сложных процессов в региональной экономике – инвестиционных, производственных, финансовых, управленческих, – и поэтому затруднительно без разработки математических моделей. При этом учет интересов нескольких экономических агентов рассматриваемой ЭС, характеризующихся рядом целевых функций, требует описания этой системы в классе многокритериальных задач. В данной работе предлагается содержательная постановка задачи оптимизации инвестиционных, производственных и финансовых потоков в экономической системе, агентами которой являются производственные предприятия и потребители региона, а также региональный управляющий (налоговый) центр. При этом возникает конфликт интересов этих экономических агентов, так как целью производителя и потребителя является максимизация прибыли, функции полезности или другого показателя эффективности, а управляющего центра – максимизация налоговых поступлений в бюджет от деятельности предприятий отрасли, что ведет к увеличению расходов производителя и потребителя и, соответственно, уменьшению прибыли или собственных средств. Таким образом, поиск компромиссных вариантов инвестирования в условиях конфликта интересов является актуальной практической задачей.
Рассмотрим следующую задачу управления экономическим развитием региона. Региональный центр организует согласованное взаимодействие региональных социально-экономических комплексов – промышленного, социального, финансово-кредитного – путем увязки интересов обобщенного потребителя (социальный сектор) и обобщенного производителя (сектор бизнеса) через выделение им дотаций, субсидий и т.п. Предположим, что выделение дотаций производится из сумм налоговых поступлений как производителя (налоги на добавленную стоимость, имущество, прибыль, страховые взносы в социальные фонды – как основных видов налоговых затрат производителя), так и потребителя (налог на доходы физических лиц и др.). Выделение дотаций способствует одновременно развитию производства, повышению платежеспособного спроса на производимую продукцию, что, в свою очередь, способствует росту налоговых поступлений в бюджет региона. Предположим, кроме того, что выполняются следующие упрощающие предположения:
1) сумма дотаций обобщенному потребителю и обобщенному производителю – это часть налоговых отчислений в регион дотируемых предприятий малого бизнеса, конкурентоспособных отраслей экономики региона, сферы услуг и др.;
2) фонд оплаты труда (ФОТ) работников производственной сферы характеризует среднюю трудоемкость производства и определяется как заданная доля выручки от продажи продукции;
3) выпуск по каждому виду продукции не выше спроса на нее и не выше максимальной средней производительности основных средств;
4) текущие финансовые средства производителя и потребителя неотрицательны;
5) горизонт планирования разделяется на три временных этапа – этап инвестирования средств в производство (t = 0) и запуск механизма перераспределения кредитно-инвестиционного и бюджетного ресурсов; этап производственной, инвестиционной и финансовой деятельности системы «обобщенный потребитель – обобщенный производитель – регулирующий центр»; заключительный момент t = T горизонта планирования.
Заметим, что первая и вторая предпосылки стимулируют использование внутренних ресурсов региона и заинтересованность работников предприятий (являющихся одновременно и потребителями) в росте производства, а третья – исключает перепроизводство, увязывая интересы потребителей и производителей. Дотации производителям увеличивают их прибыль, а потребителям – доход, обеспечивая платежеспособный спрос.
С учетом приведенных предпосылок, математическая модель оптимального управления региональным социально-экономическим развитием может быть представлена в следующем виде:
Уравнения движения:
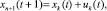
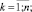
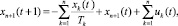
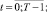
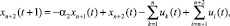 t = 0;
t = 0;
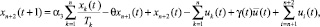
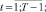
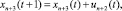
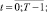 (1)
(1)
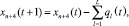 t = 0;
t = 0;
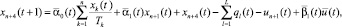
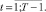
Начальные условия:
xi(0) = 0, 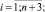 xn+4(0) = M0.
xn+4(0) = M0.
Ограничения:
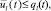
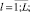 0 ≤ ukj(t) ≤ δkj(t)xk(t),
0 ≤ ukj(t) ≤ δkj(t)xk(t), 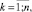
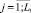
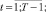
u n+1(0) ≤ I0; x n+2(t) ≥ 0; x n+4(t) ≥ 0, 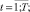 ui(0) ≥ 0,
ui(0) ≥ 0, 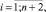
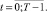
Целевые функции потребителя, производителя и управляющего центра:
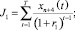
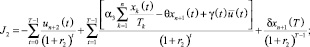
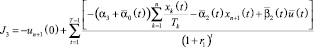
– дисконтированные суммы собственных средств каждого из указанных экономических агентов.
В приведенной модели введены следующие управляющие и фазовые переменные: uk(t) (k = 1, …, n; t = 1, …, T–1) – стоимость приобретаемых активов k-го типа; ukj(t) (t = 1, …, T–1) – объем продаж всей продукции j-го вида, произведенной на k-м типе актива; un+1(t), un+2(t) (t = 0, …, T–1) – инвестиции производителей и дотации им; xk(t) (k = 1, …, n; t = 0, …, T) – накопленная стоимость активов k-го типа; xi(t) (i = n + 1, …, n + 4; t = 0, …, T) – соответственно остаточная стоимость всех производственных активов, текущие средства производителей, накопленные до момента t инвестиции производителей, текущие средства потребителей; 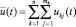 – объем продаж всей продукции, произведенной на k-м типе производственного актива;
– объем продаж всей продукции, произведенной на k-м типе производственного актива; 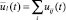 – объем продаж всей продукции l-го вида, произведенной на k-м типе актива (i – тип актива, производящих l-й вид продукции, совпадающий с j-м). При этом переменные xi(t) относятся к моменту t, а ul(t), ukj(t) – к моменту t + 1.
– объем продаж всей продукции l-го вида, произведенной на k-м типе актива (i – тип актива, производящих l-й вид продукции, совпадающий с j-м). При этом переменные xi(t) относятся к моменту t, а ul(t), ukj(t) – к моменту t + 1.
Параметры, использованные в (1), имеют следующий содержательный смысл: α1, α2, α3 – ставки налога на добавленную стоимость, на имущество и на прибыль; β(t), σ1(t), σ2(t) (t = 2, …, T) – соответственно доля выделяемой на ФОТ выручки от продажи продукции (трудоемкость), доли выделяемых на дотации поступлений в регион от налогов на имущество и на прибыль; ql(t) = ql (xn+4(t)) (t = 1, ..., T – 1) – спрос в стоимостной форме (функция от xn+4(t)) на l-й вид продукции; Pj(t) (t = 1, …, T–1) – стоимость единицы продукции j-го вида; Tk, Vkj, ck(t) (t = 0, …, T–1) – срок службы, производительность по продукции j-го вида и стоимость единицы актива k-го типа; δkj(t) = Pk(t)Vkj/ck(t) – относительная эффективность производственного актива k-го типа, производящего j-й вид продукции; n, L, mk – число типов производственных активов, различных видов продукции и число различных видов продукции, производимой на k-м типе актива; T, r1, r2 – соответственно срок действия (горизонт планирования) и ставки дисконтирования инвестиционного проекта (ИП); δ – доля остаточной стоимости всех производственных активов от их балансовой стоимости на момент t = T; M0, K0, L0 – средства потребителей и производителей в момент t = 0 и наибольшая дотация в момент t = 1. Кроме того, на основе указанных параметров используются следующие их комплексы:
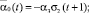
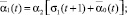
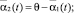
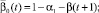
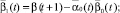
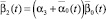
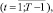
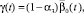
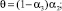
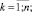
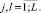
Первое и второе ограничения модели (1) содержательно описывают условия ограниченности объемов производимой в системе продукции (в стоимостном выражении) либо уровнем спроса на нее, либо производительными возможностями для всех видов основных средств и производимой продукции в любой момент реализации производственно-инвестиционного проекта. Третье условие ограничивает объем инвестиционного ресурса в начальный момент времени. Последняя группа ограничений является естественными условиями неотрицательности значений указанных в них групп переменных в любой момент реализации производственно-инвестиционного проекта.
Модель (1) позволяет находить оптимальные распределения инвестиций по видам ОПФ, объемы производимой на них продукции разного типа, а также оптимальные значения внешних источников финансирования – кредитов и дотаций – с точки зрения максимизации чистой приведенной стоимости производственного предприятия, с учетом интересов региональных органов управления и потребительского сектора. Модель (1) представляет собой линейную задачу оптимального управления, учитывающую все основные виды деятельности производственного предприятия – инвестиционную, операционную и финансовую, что позволяет решить прямую задачу оптимального производственно-инвестиционно-финансового планирования в ее полной постановке: по заданному распределению стоимостей ОПФ и стоимостей производимой на них многономенклатурной продукции найти оптимальное распределение инвестиций, объемы производства продукции и объемы необходимого для обеспечения платежеспособности основных региональных экономических субъектов финансового ресурса.
Отметим, что модель (1), в отличие от моделей, приведенных в работах [3–5], не использует принцип чистых отраслей, когда предполагается, что на одном виде актива производится единственный вид продукции.
Пусть, в дополнение к указанным выше содержательным условиям рассматриваемой задачи, предполагается, что производственные предприятия региона могут брать кредит в банке для расширения возможностей финансирования своей производственно-инвестиционной деятельности, а значит, и повышения значений своего критерия качества (дисконтированной суммы собственных средств). При этом известны средние значения сумм выданных кредитов, процентных годовых ставок по ним и сроки кредитов. Кроме того, по условиям кредитных договоров предполагаются выплаты суммы основного долга равномерными платежами ежемесячно, а суммы процентов начисляются на оставшуюся часть долга и выплачиваются также помесячно. Тогда средняя сумма S(t) ежемесячных платежей за кредит описывается следующей формулой:
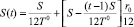
(t = 1, ..., T = 12T0), (2)
где первое слагаемое в формуле (2) – средняя сумма основного долга, а второе – средняя сумма процентов по кредиту, начисленная за месяц t; T = 12T0 – средний срок кредита в месяцах (T0 – соответственно срок кредита в годах); S – сумма выданного кредита. При этом из правых частей уравнений динамики в (1) для фазовой переменной xn+2(t) следует вычесть сумму S(t) ежемесячных кредитных платежей, заменив ее на выражение правой части формулы (2) для исключения величины S(t) из модели.
Заметим, что формулу (2) удобнее представить в виде
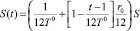
(t = 1, ..., T = 12T0). (2′)
Если предполагать, что выдаваемые кредиты являются целевыми, например могут быть потрачены лишь на приобретение ОПФ, участвующих в производстве, то к ограничениям МЗЛП (1) добавляется еще одно очевидное ограничение
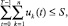 (3)
(3)
означающее, что стоимость всех ОПФ, приобретенных в течение срока действия проекта (или срока кредита), не превышает фиксированной суммы кредита S. Если же, кроме того, ставится задача о выборе оптимальной суммы кредита в задаче (1)–(3), то величину S следует рассматривать как независимую переменную, дополнив условие (3) естественными ограничениями
0 ≤ S ≤ Smax, (4)
где Smax – максимально возможная кредитная сумма.
Представленная модель (1) оптимального управления финансово-инвестиционным развитием региональных ЭС (и ее модификации (1)–(2), (1)–(3) и (1)–(4)), с учетом баланса интересов нескольких участников региональной экономической системы, позволяет осуществлять системный анализ региональной экономики путем определения оптимального объема инвестиций, производства продукции нескольких видов конкурентоспособных отраслей экономики региона, финансирование указанной деятельности, дотирование производителей и потребителей, что, в свою очередь, позволяет поддерживать стабильный уровень производства, а также уровень жизни населения в регионе. Нетрудно убедиться, что модели (1)–(3) и (1)–(4) также относятся к классу многокритериальных многошаговых задач. В случае линейности функций спроса ql(t) по фазовой переменной xn+4(t) указанные модели являются многошаговыми задачами линейного программирования, что дает возможность применять для ее решения эффективные численные методы.
Cогласно [6], ММЗЛП (1) (а также описанные выше ее обобщения) эквивалентна однокритериальной линейной задаче с теми же ограничениями и максимизацией свертки целевых критериев
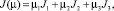
где 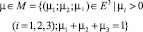 – вектор параметров, E3 – трехмерное евклидово пространство. Многокритериальный анализ описываемой экономической системы (поиск Парето-оптимальных инвестиционных стратегий и достижение компромисса интересов экономических агентов) – регионального управляющего (налогового) органа, производственного сектора и обобщенного потребителя в регионе – можно осуществлять с помощью разработанного авторами комплекса в виде пакета прикладных программ [2] и описанной в работе [1] системы поддержки принятия решений. Указанный комплекс показал свою эффективность при анализе ряда инвестиционных проектов регионального уровня [3–5].
– вектор параметров, E3 – трехмерное евклидово пространство. Многокритериальный анализ описываемой экономической системы (поиск Парето-оптимальных инвестиционных стратегий и достижение компромисса интересов экономических агентов) – регионального управляющего (налогового) органа, производственного сектора и обобщенного потребителя в регионе – можно осуществлять с помощью разработанного авторами комплекса в виде пакета прикладных программ [2] и описанной в работе [1] системы поддержки принятия решений. Указанный комплекс показал свою эффективность при анализе ряда инвестиционных проектов регионального уровня [3–5].
Библиографическая ссылка
Медведев А.В., Победаш П.Н. МНОГОКРИТЕРИАЛЬНАЯ МНОГОШАГОВАЯ ЛИНЕЙНАЯ МОДЕЛЬ ФИНАНСОВО-ИНВЕСТИЦИОННОГО ПЛАНИРОВАНИЯ В РЕГИОНАЛЬНЫХ ЭКОНОМИЧЕСКИХ СИСТЕМАХ // Фундаментальные исследования. 2016. № 7-2. С. 382-386;URL: https://fundamental-research.ru/ru/article/view?id=40518 (дата обращения: 12.03.2026).



