Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кобрунов А.И. 1 Кунцев В.Е. 1 Мотрюк Е.Н. 1

---

1 ФГБОУ ВО «Ухтинский государственный технический университет»

Работа посвящена разработке метода расчета пространственного распределения фильтрационного сопротивления проницаемого пласта нефтегазового месторождения на основе гидродинамической томографии. Приведены принципы гидродинамической томографии как развития метода гидродинамического прослушивания, отличающегося использованием веерной томографической системы наблюдений. Анализ данных основан на динамике реперной точки кривой восстановления давления и интервальных времен ее движения между парами скважин в системе наблюдений. Разработан алгоритм прямой задачи расчета интервальных времен по заданному распределению коэффициента пьезопроводности. Описана вычислительная схема решения обратной задачи на основе разработанного алгоритма, включающая в себя: итерационный процесс уточнения параметров пьезопроводности; расчет параметра релаксации, обеспечивающего сходимость процесса; контроль невязки и правила остановки итерационного процесса. Выполненная программная реализация алгоритма гидродинамической томографии протестирована рядом разноплановых модельных примеров, демонстрирующих работоспособность и эффективность метода гидродинамической томографии.

Статья в формате PDF

0 KB

гидродинамика

томография

интервальное время

коэффициент пьезопроводности

итерационный процесс

оптимизация

сходимость

1. Кобрунов А.И. Математическая модель томографии на давлениях при контроле за разработкой нефтяных месторождений // Известия Коми научного центра Уро РАН. – 2012. – Вып. 412. – С. 82–86.

2. Кобрунов А.И. Теоретические основы гидродинамической томографии // Геофизический журнал. – 2015. – Вып. 2. – С. 27–34.

3. Кобрунов А.И., Кунцев В.Е., Мотрюк Е.Н. Технология оценки связности скважин на основе модели эксплуатации месторождения // Фундаментальные исследования. – 2015. – № 6–3. – С. 452–456.

4. Кобрунов А.И. Математические основы теории интерпретации геофизических данных: учебное пособие. – Ухта: УГТУ, 2007. – 286 с.: ил.

5. Колмогоров А.Н. Элементы теории функций и функционального анализа // Колмогоров А.Н., Фомин С.В. – М.: Наука, 1976. – 543 с.

6. Краснов В.А., Иванов В.А., Хасанов М.М. Помехоустойчивый метод оценки связности пласта по данным эксплуатации месторождений // Российская техническая нефтегазовая конференция и выставка SPE по разведке и добыче (Москва, 16–18 октября 2012 года). – SPE. – 162053.

Гидродинамическая томография позволяет проводить прогноз пространственного распределения фильтрационного сопротивления проницаемого пласта на основании принципов томографии, используя данные гидродинамического прослушивания и анализ динамики реперной точки кривой восстановления давления [1, 2].

Применение технологии гидродинамической томографии позволяет получать детальную пространственную информацию о распределении фильтрационного сопротивления в межскважинном пространстве проницаемого пласта. Технология томографии заключается в обработке и анализе веерных измерений интервальных времен наступления реакции в скважинах-приемниках на изменение режима давления в скважинах-источниках.

Практическая реализация технологии гидродинамической томографии может быть основана как на прямых измерениях интервальных времен распространения характерных точек кривых восстановления давления в веерной системе из нескольких скважин, так и на косвенных – анализе истории разработки месторождения. В первом случае необходимые исходные данные для реализации томографической обработки информации берутся из прямого эксперимента на месторождении – возникает активная модификация гидродинамической томографии. Для прямого эксперимента гидродинамической томографии необходима реализация достаточно затратной и технологически трудоемкой схемы действий. Во втором случае данные веерной системы наблюдений по выбранной сети скважин, необходимые для выполнения томографического моделирования, синтезируются исходя из построенной модели месторождения по данным истории разработки в виде динамики дебита и нагнетания по всем скважинам в пределах выбранного временного интервала [3, 6]. Такая технология гидродинамической томографии называется пассивной гидродинамической томографией. Прогноз томографических данных реализуется вычислительным экспериментом над построенной математической моделью месторождения в рамках гипотезы о характере ее основных компонентов.

Для решения задачи нахождения пространственного распределения фильтрационного сопротивления проницаемого пласта необходимо использовать метод последовательных приближений относительно распределения коэффициента пьезопроводности, организованных в итерационный процесс решения интегрального уравнения, характеризующего динамику движения реперной точки по исходным данным интервальных времен движения между парами скважин. Перед началом вычислений выдвигается предположение о форме пространственного распределения коэффициента пьезопроводности по сетке месторождения и вытекающими из него траекториями и временами движения особых точек распространения давления. Затем вычисляются поправки к этому пространственному распределению, обеспечивающие наилучшее приближение интервальных времен, полученных в результате моделирования процесса движения особых точек кривой восстановления давления к наблюдаемым интервальным временам динамики давления между парами скважин (источник-приемник). Для рассчитанного таким образом пространственного распределения коэффициента пьезопроводности вычисляются новые траектории и соответствующие им интервальные времена. Далее, если совпадение моделируемых интервальных времен с наблюдаемыми удовлетворительное, то итерационный процесс последовательных приближений заканчивается и решение задачи найдено. В противном случае процесс расчета интервальных времен повторяется с использованием нового распределения коэффициента пьезопроводности, которое будет использоваться в качестве начального приближения.

Рассмотрим поэтапно вычислительную схему гидродинамической томографии. Для дискретизации процесса на область рассматриваемого месторождения S накладывается сетка размерностью X×Y. Ячейки сетки обозначаются парой индексов {(i, j)} так, что каждая точка области ξ в сеточном представлении однозначно идентифицируется своей парой индексов ξ(i, j) = (i, j). В области S задано начальное распределение коэффициента пьезопроводности k(ξ) = k(i, j). На сетке месторождения расположены скважины, которые между собой образуют Q пар, где m = 1–M – количество скважин-источников сигнала и n = 1–N – количество скважин-приемников сигнала (Q = N×M). Распространение возмущения для каждой пары скважин происходит по траекториям Lq = L(ξ_qm, ξ_qn), имеющим начало в точке ξ_qm = (i, j)qm и окончание в точке ξ_qn= (i, j)qn. Траектории обозначаются индексом q = 1–Q и время движения возмущения вдоль Lq равно τ_q. Текущая координата сети вдоль пути Lq обозначается переменной ξq = (i, j)q. Обозначим через l(ξ) путь, который проходит волна от начала ξqm = (i, j)qm до точки ξ_q на траектории Lq. Время распространения движения волны τ_q рассчитывается при помощи следующего оператора:

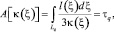(1)

что в дискретном представлении:

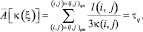(2)

На основе соотношения (2) строятся кратчайшие траектории движения особых точек Lq согласно принципу Беллмана с условиями минимизации на интервальные времена τ_q. Полученные траектории и используем в дальнейших расчетах.

Пусть 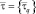есть наблюдаемое время распространения давления (точки перегиба кривой восстановления давления), измеренное в результате эксперимента и которое соответствует пространственному распределению коэффициента пьезопроводности k(ξ) + Δk(ξ). Необходимо найти Δk(ξ) такое, чтобы рассчитанное Δτ_q было максимально приближено к 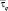. Тогда разность Δτ_q наблюдаемого и рассчитанного интервальных времен получаем в виде соотношения, которое выражается из нескольких приближенных равенств:

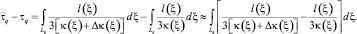(3)

Меняя знак, получаем

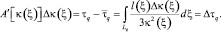(4)

Оператор A′[k(ξ)] суть производная Фреше [5] к оператору A[k(ξ)] в «точке» k(ξ). A′[k(ξ)] – линейный оператор, действующий на вектор Δk(ξ). Формулы (3) и (4) получены в предположении того, что величина Δk(ξ) настолько мала, что произведение (k(ξ) +  Δk(ξ))•k(ξ) ≈ k(ξ)² и траектории Lq = L(ξqm, ξqn) для пьезопроводности k(ξ) + Δk(ξ) и k(ξ) с достаточной точностью совпадают.

Уравнение (4) в дискретной форме выглядит следующим образом:

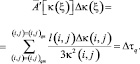(5)

Если количество узлов сети в траектории q равно Nq, то размерность вектора Δk(i, j) равна

.

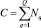Областью значения преобразования (5) служит вектор Δτ = {Δτ_q} размерности Q. После того как вектор Δk(i, j) найден, следующее приближение к распределению коэффициента пьезопроводности определяется правилом

k¹(ξ) = k(ξ) + Δk(ξ). (6)

Вычислительной основой для решения задачи (5) относительно вектора Δk(i, j) в точках ξ(i, j) траекторий Lq = L(ξqm, ξqn) служит итерационный процесс, на z + 1 итерации, имеющий вид

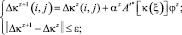(7)

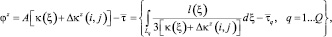(8)

где φ^z – разница между наблюдаемыми интервальными временами и временами, рассчитанными на итерации z.

Нулевое приближение принимаем равным Δk⁰(i, j) = 0.

Числовой параметр α^z – параметр релаксации, подбираемый на каждом шаге так, чтобы итерационный процесс (7) сходился [4]:

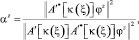(9)

где A′*[k(ξ)] – сопряженный к A′[k(ξ)] оператор, определяемый условием для – мерного вектора y = {y_q, q = 1–Q}:

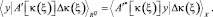(10)

Здесь X – функциональное пространство для распределения приращения к коэффициенту пьезопроводности Δk(ξ). В дискретном представлении для нашего случая это пространство R^С (где C – размерность Δk(i, j) и Q – размерность y), а условие (10) примет вид

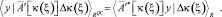(11)

Подставляя в уравнение (11) выражение (5), получим

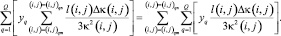(12)

Для того чтобы приведенное равенство имело смысл, следует специальным образом организовывать суммирование в правой части, что в конечном итоге определяет вид оператора .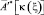

Значение оператора 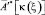на Q-мерном векторе y есть значения вектора g(i, j) для индексов (i, j) = {(i, j)qm...(i, j)qn, q = 1–Q}. Для индексов (i, j) выделяются значения q(i, j), определяющие траектории Lq, в интервалы которых попадают эти индексы. Далее конструируем выражение для вычисления значения сопряженного оператора на векторе y:

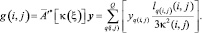(13)

Здесь lq(i, j)(i, j) – это длина участка траектории Lq от начальной точки до точки (i, j), в которой выполняется расчет g(i, j). Уравнение (13) при y = φ^z примет вид

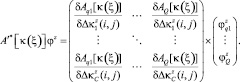(14)

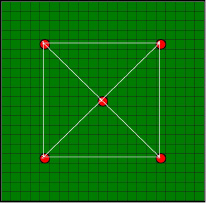а б

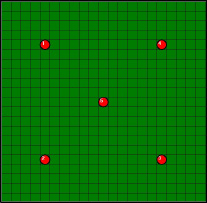
Рис. 1. а – сетка скважин и нулевое приближение среды; б – траектории движения сигнала между скважинами Lq на первой итерации

После того как итерационный процесс завершился согласно условию в (7) и найдено решение Δk(i, j) уравнения (5) для (6), служащее новым приближением для распределения пьезопроводности в узлах, определяемых траекториями вдоль сети, на области S рассчитываются новые траектории , на основе которых весь процесс повторяется.

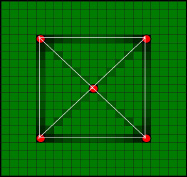
Приведем пример работы алгоритма гидродинамической томографии на примере тестового месторождения. В качестве примера рассмотрим модель месторождения, на которой расположены 5 скважин. Для нулевого приближения распределения фильтрационного сопротивления сгенерирована однородная среда k⁰(ξ) (рис. 1). Заданы тестовые наблюдаемые интервальные времена между парами скважин, Q = 20. На первой итерации по нулевому приближению находим траектории движения возмущения Lq (рис. 2) между парами скважин и рассчитываем соответствующие этим траекториям интервальные времена τ_q.

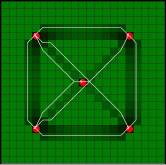
После завершения итерационного процесса и нахождения Δk(i, j), по формуле (6) определяем новые значения (рис. 2, а). На рис. 2, б представлен график динамики относительной погрешности φ между тестовыми и рассчитанными интервальными временами внутри итерационного процесса (7) на первой итерации. На рис. 3, а и б представлены результаты оптимизации среды после двух и десяти итераций соответственно.

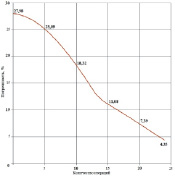а б

Рис. 2. а – результаты работы оптимизационного процесса (7) на первой итерации; б – динамика средней относительной погрешности φ на первой итерации

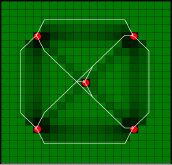а б

Рис. 3. а – результаты оптимизационного процесса на второй итерации; б – результат оптимизации среды после десяти итераций

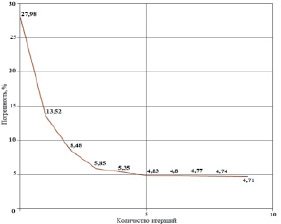
Рис. 4. Динамика относительной погрешности по Δτ

На рис. 4 представлен график динамики средней относительной погрешности по Δτ после нахождения траекторий движения сигнала между скважинами (3). Далее происходит оценка этой величины и принятие решения о продолжении процесса вычислений (7).

Результаты расчета пространственного распределения фильтрационного распределения вдоль траекторий движения сигнала между парами скважин для тестовой модели показали, что выбранный алгоритм оптимизации может быть применен для поиска k = k⁰ + Δk на основе выбранного начального приближения k⁰. Следующим шагом необходимо разработать метод интерполяции значений Δk на всю сетку рассматриваемого месторождения с учетом информации о расположении и качестве имеющихся начальных данных. Для реализации этого алгоритм будет основан на теории нечетких множеств.

Библиографическая ссылка