Целесообразность применения автоматизированных систем управления дорожным движением неоднократно обосновывалась в теоретических исследованиях, подтверждалась при практической реализации и в настоящее время не вызывает сомнений. Разработано большое количество математических моделей распределения транспортных потоков по сети, часть из которых легла в основу программных продуктов для автоматизированного решения широкого спектра задач по организации движения. Однако рост интенсивности движения транспортных средств и развитие инфраструктуры городов выдвигают новые требования к организации движения. А развитие компьютерных технологий дает новые возможности для решения проблем в рамках интеллектуальных транспортных систем.
Основной причиной заторных ситуаций является неэффективная организация движения в узловых точках сети. Высокая интенсивность движения транспортных потоков требует строительства кольцевых и многоуровневых пересечений. Для автоматизированного управления дорожным движением с учетом всех типов узловых точек сети требуется разработка соответствующих математических моделей движения транспортных средств, методов мониторинга и хранения соответствующей информации, методов автоматизированного извлечения необходимой информации из динамически изменяющейся матрицы корреспонденций при управлении транспортными потоками.
Моделирование движения на кольцевых пересечениях
По сравнению с крестообразными пересечениями и Т-образными примыканиями в одном уровне кольцевые пересечения являются более эффективными типами пересечений с меньшим числом конфликтных точек. Кроме того, они отличаются безопасными скоростями движения, лучшей обзорностью и более простыми условиями для восприятия водителем дорожной ситуации [2]. Для моделирования движения на кольцевых пересечениях применяются два основных методологических подхода: эмпирический и аналитический [1]. Эмпирический основан на установлении регрессионных зависимостей по экспериментальным данным. Один из таких методов был разработан Транспортной и дорожной исследовательской лабораторией (TRRL – Transport and Road Reserch Laboratory) еще в семидесятых годах прошлого столетия и применяется в Великобритании.
Аналитические методы основаны на установлении вида статистического распределения интервалов между транспортными средствами и дальнейшего применения методов теории вероятностей и теории случайных процессов для определения показателей эффективности организации движения на кольцевом пересечении. В качестве основных показателей эффективности организации движения на пересечениях в одном уровне HCM (Highway Capacity Manual) называет задержки транспортных средств, с учетом которых классифицируются уровни обслуживания (level of service). С этой целью применяли теорию массового обслуживания Поллажек (Pollaczek), Кинчин (Khintchine), Траутбек (Troutbeck), Хейдман (Heidemann) и Вегман (Wegmann) и другие исследователи [4].
Многие программные продукты (CORSIM, Integration, Simtraffic, Paramics, VISSIM) позволяют использовать при имитационном моделировании движения транспортных потоков по сети аналитические модели отдельных изолированных кольцевых пересечений. Это дает возможность для более точного расчета времени движения по отдельным участкам сети, прогнозирования интенсивности движения, вероятностей образования заторов, длины очередей транспортных средств, а также, как следствие, расчета расхода топлива, эмиссии вредных веществ и уровня шума.
Более детальное моделирование кольцевых пересечений, с учетом геометрических параметров, позволяют проводить такие программные продукты, как ARCADY, RODEL, SIDRA, KREISEL или GIRABASE [5].
Аналитическая модель движения транспортных средств на кольцевых пересечениях
В случае применения аналитических методов для достижения необходимой точности важно выбрать такое статистическое распределение интервалов между транспортными средствами в потоке, которое при минимальном наборе исходных данных позволяло бы делать адекватные прогнозы. В разработанной автором мезоскопической математической модели TIMeR_Mod (Transportation Intelligent Mesoscopic Real-time Model) учитывается пополосное движение транспортных средств и рассчитываются задержки в местах слияния и пересечения любого числа транспортных потоков. Конфликтные точки в модели классифицируются на узловые точки I типа (соответствует нерегулируемому пересечению потоков) и II типа (соответствует пересечению транспортных потоков со светофорным регулированием), а каждый тип пересечения в одном уровне (многополосные пересечения нерегулируемых перекрестков и перекрестков с жестким светофорным регулированием, кольцевые пересечения) определяется как совокупность узловых точек.
Авторами экспериментально доказано, что хорошую согласованность между эмпирическим и теоретическим распределением интервалов по времени между транспортными средствами в потоке при различной интенсивности движения дает обобщенный закон Эрланга. Значительным плюсом этого распределения является то, что он позволяет с помощью метода псевдосостояний получать точные значения средних характеристик показателей эффективности системы массового обслуживания, не прибегая к имитационному моделированию, без округлений и приближений в расчетах.
При принятии данной гипотезы для расчета задержек в конфликтных точках на кольцевом пересечении автором разработан приведенный ниже аналитический аппарат [4]. Расчет задержек в каждой конфликтной точке для каждой полосы движения определяется отдельно. Исходными данными для модели являются:
– параметры k, λ0, λ1, ..., λ k–1 обобщенного закона Эрланга для выбранного потока A, входящего в конфликтную точку;
– параметры kj, λ0j, λ1j, ..., λ kj–1,j обобщенного закона Эрланга для каждого из L конфликтных для потока A транспортных потоков;
– Т0 – приемлемый временной интервал между автомобилями в конфликтных потоках для продолжения движения транспортными средствами потока A.
Для определения перечисленных выше исходных данных необходимо получить статистическую зависимость между величиной интервалов по времени между подряд идущими транспортными средствами в потоке и частотой их появления. Это возможно сделать, например, с помощью видеомониторинга.
Пусть
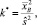
где 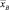 – выборочная средняя случайной величины; T – интервалов между следующими подряд по одной полосе автомобилями;
– выборочная средняя случайной величины; T – интервалов между следующими подряд по одной полосе автомобилями; 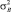 – выборочная дисперсия случайной величины T. Параметр k = [k*] + 1 – целое число, большее k*. Экспериментальные исследования показали, что значение k* для случайной величины T не превышает четырех.
– выборочная дисперсия случайной величины T. Параметр k = [k*] + 1 – целое число, большее k*. Экспериментальные исследования показали, что значение k* для случайной величины T не превышает четырех.
С помощью метода моментов и средств алгебры разработан способ расчета параметров обобщенного распределения Эрланга порядка k, для k ∈ {1, 2, 3, 4}, по результатам мониторинга транспортного потока:
– при k = 1: 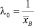 (показательное распределение);
(показательное распределение);
– при k = 2: 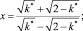
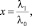 тогда
тогда
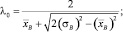
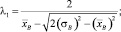
– при k = 3. Пусть λ1 = x•λ0; λ2 = x•λ1 = x2•λ0, тогда
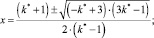
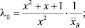
– при k = 4. Пусть λ1 = x•λ0; λ2 = x•λ1 = x2•λ0; λ3 = x•λ2 = x3•λ0, тогда
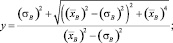
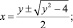
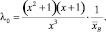
Средняя задержка (в секундах) в данной конфликтной точке одного транспортного средства выбранного второстепенного направления A с учетом очереди равна
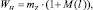 (1)
(1)
где
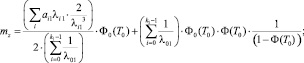 (2)
(2)
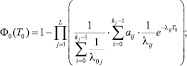 (3)
(3)
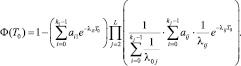 (4)
(4)
Формула (2) определяет среднее время ожидания возможности продолжить движение через данную конфликтную точку первым в очереди автомобилем выбранного потока A.
Среднее число транспортных средств в очереди у конфликтной точки на кольцевом пересечении в выбранном направлении A:
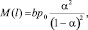 (5)
(5)
где 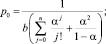
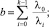
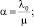
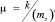
Кольцевое пересечение в модели TIMeR_Mod представляет собой множество L конфликтных точек и дуг между ними. Функция транспортных затрат на кольцевом пересечении для данного направления A определяется как сумма средних задержек транспортных средств этого направления при прохождении конфликтных точек и среднего времени, необходимого на преодоление расстояния между соседними конфликтными точками.
Пусть τl(y) – затраты на прохождение дуги y между двумя конфликтными точками в направлении A; τlz(y) – средняя задержка в данной конфликтной точке в направлении A. Тогда функция транспортных затрат потока A на кольцевом пересечении рассчитывается следующим образом:
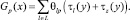 (6)
(6)
Величина θlp принимает значение 1, если поток A проходит через конфликтную точку l ∈L, и равна 0 – в противном случае.
Затраты τl(y) на прохождение дуги y между двумя конфликтными точками равны
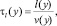 (7)
(7)
где l(y) – длина дуги y; v(y) – средняя скорость движения по дуге y; в качестве τlz(y) следует брать величину WН, рассчитываемую по формуле (1).
Функция транспортных затрат на кольцевом пересечении, определяемая по формуле (6), позволяет рассматривать кольцевое пересечение как часть транспортной сети при автоматизированном решении транспортных задач глобального характера.
Заключение
Преимущество метода определения транспортных затрат на кольцевых пересечениях, предложенного выше, перед существующими состоит в том, что он применим для потоков как с низкой, так и с высокой интенсивностью движения, учитывает распределение потоков по полосам, позволяет прогнозировать изменение величины задержек при изменении схемы организации или интенсивности движения. Благодаря аналитическим методам расчета результат получается мгновенно. Это позволяет использовать данный метод в интеллектуальных транспортных системах для автоматизированного решения задач организации движения на улично-дорожной сети в режиме реального времени.
Работа выполнена при поддержке РФФИ и администрации Краснодарского края, проект р-юг-а -16-48-230720.
Библиографическая ссылка
Наумова Н.А., Данович Л.М., Карачанская Т.А. АНАЛИТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ АВТОТРАНСПОРТНЫХ СРЕДСТВ НА КОЛЬЦЕВЫХ ПЕРЕСЕЧЕНИЯХ // Фундаментальные исследования. 2016. № 6-1. С. 94-97;URL: https://fundamental-research.ru/ru/article/view?id=40378 (дата обращения: 07.03.2026).



