Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кузнецов Ю.А. 1 Семенов А.В. 1 Груздева Е.Е. 1

---

1 ФГАОУ ВО«Национальный исследовательский Нижегородский государственный университет им. Н.И. Лобачевского»

В работе рассматриваются математические модели экономического роста на бесконечном горизонте планирования с учетом различных экологических факторов и доступных природных ресурсов (как исчерпаемых, так и возобновляемых). Рассматриваемые модели по своей постановке являются задачами оптимального управления, исследование которых опирается на принцип максимума Понтрягина. Предлагаются варианты обобщения одной экономико-математической модели роста путем включения в уравнения динамики капитала и доступного возобновляемого природного ресурса экстерналий, связанных с использованием данного ресурса. Включение внешних эффектов (экологических экстерналий) в математические модели экономического роста необходимо для адекватного отражения реальной действительности. Рассматриваемые модели описывают динамику развивающихся экономических систем, находящихся в условиях сильного воздействия внешних отрицательных эффектов, связанных с состоянием окружающей среды.

Статья в формате PDF

0 KB

экономико-математическое моделирование

экономический рост

экстерналии

1. Бобылев С.Н. Экономика природопользования: учебник/ С.Н. Бобылев, А.Ш. Ходжаев – М.: Инфра-М, 2007. – 501 с.

2. Голуб А.А. Экономика природных ресурсов/ А.А. Голуб, Е.Б. Струкова – М.: Аспект Пресс, 2001. – 319 с.

3. Кузнецов Ю.А. Человеческий капитал, производительность труда и экономический рост// Экономический анализ: теория и практика. I. – 2012. – №43(298). – C. 2–17; II. – 2012. – №44(299). – C. 2–14.

4. Кузнецов Ю.А. Модель экономического роста с учетом накопления человеческого капитала по схеме «learning-by-doing». I/ Ю.А. Кузнецов, Т.С. Гребенкина// Вестник Нижегородского государственного университета им. Н.И. Лобачевского. – 2013. – №2(1). – C. 142–151.

5. Кузнецов Ю.А. Обобщенная модель экономического роста с учетом накопления человеческого капитала/ Ю.А. Кузнецов, О.В. Мичасова// Вестник Нижегородского государственного университета им. Н.И. Лобачевского. I. – 2010. – №1. – C. 168–175; II. – 2010. – №2. – C. 158–165; III. – 2010. – №3(1). – С. 177–190.

6. Кузнецов Ю.А. Математическое моделирование оптимального использования невозобновимых природных ресурсов/ Ю.А. Кузнецов, А.В. Семенов, М.Н. Власова// Экономический анализ: теория и практика. – 2012. – №32 (287). – С. 45–57.

7. Ровенская Е.А. Модель оптимального экономического роста с учетом экологических факторов// Экономика и математические методы. – 2012. – Т.48. – №4. – С. 80–89.

8. Эндрес А., Квернер И. Экономика природных ресурсов. – СПб.: Питер, 2004. – 256 с.

9. Antoci A., Galeotti M., Russu P. Poverty trap and global indeterminacy in a growth model with open-access natural resources// Journal of Economic Theory. – 2011. – Vol.146, №2. – P. 569–591.

10. Caetano M.A.L., Gherardi D.F.M., Yoneyama T. Optimal Resource Management Control for CO2 Emission and Reduction of the Greenhouse Effect// Ecological Modelling. – 2008. – Vol. 213, №1. – P. 119–126.

11. Hotelling H. The Economics of Natural Resources// Journal of Political Economy. – 1931. – Vol.39, №2. – P.137–175.

12. SolowR.M. Intergenerational Equity and Exhaustible Resources// Review of Economic Studies. – 1974. Vol. 41. Symposium on the Economics of Exhaustible Resources. – P.29–45.

13. Stiglitz J.E. Growth with Exhaustible Natural Resources: Efficient and Optimal Growth Paths// Review of Economic Studies. – 1974. – Vol.41. Symposium on the Economics of Exhaustible Resources. – P.123–137.

14. Stiglitz J.E. Growth with Exhaustible Natural Resources: The Competitive Economy// Review of Economic Studies. – 1974. – Vol. 41. Symposium on the Economics of Exhaustible Resources. – P.139–152.

Экологические проблемы входят в число наиболее значимых как для развитых, так и развивающихся экономик: деградация окружающей среды тесно связана с интенсивностью экологической деятельности и достигнутым уровнем благосостояния. Вэкономике природопользования хорошо известна взаимосвязь воздействия человеческой деятельности на окружающую среду и достигнутого уровня экономического благосостояния. Она описывается так называемой экологической кривой Кузнеца: при росте дохода на душу населения уровень деградации окружающей среды сначала растет, а затем – по мере достижения определенного уровня благосостояния – он начинает снижаться (подробнее см., например, [1, 2, 8]). Так, для экономик, характеризующихся низким уровнем развития и доходов, на первый план выходят, как правило, природоэксплуатирующие секторы (добывающая промышленность, сельское хозяйство и т.д.), что приводит к росту истощения природных ресурсов и загрязнения окружающей среды. Однако по мере роста экономики, ее структурно-технологических изменений, распространения экологически чистых технологий, вступления на постиндустриальную стадию развития экологическое воздействие существенно снижается, в том числе по причине роста требований населения к экологической компоненте качества жизни [1, 2, 8].

Значительный научный интерес представляют экономико-математические модели экономического роста, учитывающие экологические факторы. Этот интерес возник достаточно давно (см., например, [11–14]), и внастоящее время исследования в этой области насчитывают десятки монографий и тысячи статей. Их обзор выходит далеко за рамки настоящей статьи. Укажем здесь только несколько сравнительно недавних публикаций, в которых содержится достаточно богатая библиография (см. [6, 7, 9, 10]).

Одна из таких моделей рассматривается в [7]. Она связана с экономическим ростом и учетом при этом качества окружающей среды. Вней используются следующие переменные и параметры: Y(t) – национальный ВВП, K(t) – запас физического капитала, C(t) – уровень потребления, E(t) – «качество» (состояние) окружающей среды в момент времени t>0, а c(t)I[0, 1] – доля ВВП, направляемая на потребление, т.е.

C(t)=c(t)Y(t), t>0. (1)

В качестве производственной функции используется производственная функция типа АК, т.е. производственная функция вида

Y(t)=AK(t), (2)

где постоянная A>0 – характеристика производительности капитала.

Динамика накопления капитала описывается уравнением

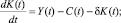K(0)=K0. (3)

где δ>0 – коэффициент выведения капитала (depreciation rate); K₀>0 – начальное значение капитала. Сучетом (1) и (2) из уравнения (3) следует

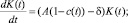K(0)=K0, (4)

«Качество» окружающей среды E(t) в момент t обратно пропорционально объёму производства с эластичностью γ>0:

E(t)=B₀Y^–γ(t)(t≥0), (5)

где B₀>0 – параметр, характеризующий зависимость качества окружающей среды от уровня ВВП. Сучетом вида производственной функции (2) формула (5) для качества окружающей среды примет вид

E(t)=B₀A^–γK^–γ(t)=BK^–γ(t)(t≥0). (6)

Оптимальное управление экономическим развитием в рассматриваемой модели осуществляется через такой выбор доли потребления 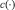, который максимизирует целевую функцию, учитывающую как совокупное потребление, так и качество окружающей среды:

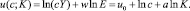
Таким образом, приходим к следующей модели экономического роста:

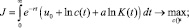
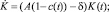
K(0)=K₀,A>δ, c(t)∈[0, 1], (7)

где r>0 – дисконтирующий множитель. Исследование полученной задачи оптимального управления опирается на принцип максимума Понтрягина.

Кроме того, в ряде моделей учитываются и экологические факторы, так в [10] представлена модель использования невозобновляемых природных ресурсов с учётом загрязнения. Пусть E(t) – количество ресурса, имеющегося в момент времени, u(t)≥0 – интенсивность добычи ресурса для экономического роста, p(t) – уровень загрязнения, A(t) – часть добычи ресурса, которая используется для борьбы против загрязнения. Вэтой модели считается, что добыча ресурса проводится государством, которое в состоянии установить верхний предел 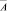величины A(t). Вмодели имеется две фазовых переменных E(t), p(t) и два управления u(t)≥0 и 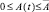. Общественный, т.е. государственный, интерес представляет функция полезности U(c(u), p), где c(u) – потребление общества за счет добычи ресурса. Таким образом, получаем следующую задачу:

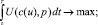
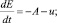
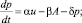
p(0)=p₀>0; E(0)=E₀>0; p(T)≥0;

E(T)≥0; u(t)≥0;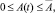

здесь α – коэффициент загрязнения среды от добычи ресурсов; β – коэффициент эффективности борьбы против загрязнения; δ – коэффициент самоочищения природы от загрязнения.

Чрезвычайно важным понятием в экономике природопользования являются экстерналии. Принятие во внимание положительных экстерналий (внешних эффектов) весьма часто можно встретить в моделях экономического роста с учетом накопления человеческого капитала, который является существенным фактором экономического роста (см., например, [3–5]). Вэкономике природопользования подавляющее число воздействий связано с возникновением отрицательных внешних эффектов (различного рода загрязнения, отходы, разрушение природных объектов, экологические ущербы и т.д.).

В настоящей работе предлагается модель экономического роста, учитывающая экстерналии окружающей среды. Данная модель является обобщением задачи, представленной в [9].

Следуя [9], рассмотрим модель экономического роста, в которой в каждый момент времени t репрезентативный агент осуществляет выпуск Y(t), используя такие факторы производства, как труд L(t), накопленный физический капитал K(t) и запас свободно доступного возобновимого природного ресурса E(t). Совокупное производство (по всей экономике) 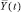нега-тивно влияет на запасы природного ресурса; однако считается, что значение 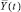экзогенно определено репрезентативным агентом, а динамика экономики подвергается негативному воздействию экстерналий окружающей среды. Предполагается, что технология производства описывается производственной функцией Кобба – Дугласа 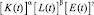, где α+β<1 и α, β, γ>0. Мгновенная полезность репрезентативного агента, зависящая от досуга 1 – L(t) и потребления C(t) выпускаемого продукта Y(t), представляет собой функцию

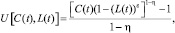
где ε, η>0 и η≠1.

Изменение капитала K(t) (предполагается для простоты, что амортизация K(t) равна нулю) соответствует следующему дифференциальному уравнению:

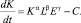
Динамика природного ресурса описывается модифицированным логистическим уравнением

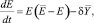
где параметр 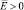фактически представляет собой допустимый разведанный запас природного ресурса (carring capacity), 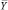– средний выпуск во всей экономике, и параметр δ>0 измеряет негативное влияние 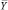на E. Таким образом, в [9] представлена следующая модель экономического роста:

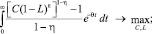
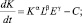
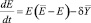
с заданными K(0) и E(0), K(t), E(t), C(t)≥0 и 1≥L(t)≥0 для каждого tI[0, +∞); θ>0 – учетная ставка.

Данная модель экономического роста с учетом экстерналий окружающей среды допускает различные расширения. Внастоящей работе предлагаются следующие три обобщения.

1.В данной модели может быть проведен учет амортизации капитала без приравнивания её нулю, что позволит более адекватно отразить действительность и описать динамику капитала в экономике. При этом уравнение динамики капитала может быть дополнено экстерналиями, связанными с природным ресурсом. Тогда модель будет иметь следующий вид:

–уравнение динамики капитала:

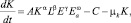μ_k≠0,

где E_a – экстерналии, связанные с природным ресурсом;

–уравнение динамики природного ресурса (типа логистического уравнения Ферхюльста – Пирла – Рида):

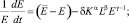
–функция полезности репрезентативного агента:

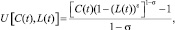
где ε, η>0 и σ≠1.

2.Введение в уравнение динамики капитала не только амортизации, но и экстерналий доступного природного ресурса. Сучетом этого модель будет выглядеть следующим образом.

–уравнение динамики капитала:

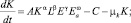μ_k≠0;

–производственная функция:

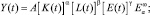
α+β<1 и α, β, γ>0;

–уравнение, касающееся свободного ресурса:

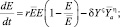
ς, η∈(0, 1), ς+η=1. (8)

Совокупное производство 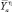во всей экономике негативно влияет на состояние (запасы) природного ресурса. Репрезентативный экономический агент действует в рамках своих интересов, и при этом осуществляемое им производство может также оказывать дополнительное негативное влияние на природный ресурс, что учитывается введением параметра Y^ς. Если же значения параметров ς=0 и η=1, то получим рассмотренную ранее модель.

3.Возможно рассмотрение в качестве репрезентативного агента и наивного агента, который считает значение Е заданным извне и не учитывает динамику данного параметра при решении задачи оптимального управления, но при этом возможно изменение спецификаций производственной функции и уравнений динамики капитала и свободно доступного природного ресурса, как в предложениях1 и 2, тогда полученная модель будет расширением первоначально рассмотренной модели, а оптимизационные задачи также могут быть сведены как к задаче о конкурентном равновесии, так и к задаче социального планировщика.

Библиографическая ссылка