Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Хлюпина М.А. 1 Исавнин А.Г. 1

---

1 Набережночелнинский институт (филиал) ФГАОУ ВО «Казанский (Приволжский) федеральный университет»

В данной работе применяются методы эконометрического анализа с целью моделирования состояния рынка недвижимости в городе Елабуга. Актуальность исследования вытекает из необходимости формализации существующих критериев оценки стоимости продаваемых квартир, так как часто на практике нет четко обоснованных критериев и моделей для её определения. Преобладает способ оценивания цены предложения квартиры, имеющий основой субъективные критерии, которые могут не совпадать у разных оценщиков. Целью работы является исследование зависимости стоимости 1 кв. метра площади квартир в городе Елабуга от характеристик этих квартир. Данные представлены агентством недвижимости «Единая Риэлтерская Компания Город». Объект исследования: вторичное жилье в городе Елабуга. Основным методом исследования является регрессионный анализ и метод Брандона.

Статья в формате PDF

0 KB

регрессионный анализ

факторы

оценка критериев

моделирование

метод Брандона

исследование зависимости

1. Зандер Е.В. Эконометрика: учебно-методический комплекс. – Красноярск, 2003. – 34 с. – С. 19–23.

2. Елисеева И.И., Курышева С.В., Костеева Т.В. и др. Эконометрика / под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М., 2007. – 576 с. – С. 347–352.

3. Исавнин А.Г., Галиев Д.Р. Модели портфельного инвестирования с применением асимметричных мер риска и генетических алгоритмов // Финансовая аналитика: проблемы и решения. – 2011. – № 48. – С. 32–38.

4. Исавнин А.Г., Фархутдинов И.И. Метод оценки экономической эффективности применения производственного аутсорсинга на автомобилестроительном предприятии России // Региональная экономика :теория и практика. – 2012. – № 13. – С. 16–21.

5. Карп Д.Б. Эконометрика: основные формулы с комментариями: учебно-методическое пособие. – Владивосток, 2004. – 50 с. – С. 40–44.

Объектом исследования выбрана недвижимость в районах города Елабуга, а предметом исследования – сложившийся уровень средней стоимости квадратного метра жилых квартир.

Данные исследования были получены от агентства недвижимости «Единая Риэлтерская Компания Город». Для проведения эконометрического моделирования рынка квартир на основе предложений о продаже квартир была построена выборка, содержащая 100 наблюдений.

Рассмотрев предложения о продаже квартир в городе Елабуга, можно сказать, что целесообразно проводить оценку продажной цены 1 кв. метра квартиры по составлению выборки и подбору возможных факторов, влияющих на стоимость жилья.

В работе рассматривается задача построения аналитической формулы средней стоимости квартиры в зависимости от факторов, влияющих на эту стоимость [1].

Зависимая переменная: Y – оценка продажной стоимости 1 кв. метра квартиры (в руб).

Независимые переменные: факторы, от которых предположительно зависит цена предложения квартиры.

Они разделяются на 2 типа:

1. Количественные:

общая площадь квартиры;

этажность дома;

этаж;

количество комнат в кв.;

площадь кухни.

2. Качественные (дихотомические):

тип дома (0 – все остальные, 1 – кирпичный);

наличие балкона/лоджии (0 – нет, 1 – есть);

расположение дома (0 – все остальное, 1 – периферия);

санузел (0 – раздельный, 1 – совместный);

наличие собственного отопления (0 – нет, 1 – есть) и др.

Далее построена матрица парных коэффициентов для устранения мультиколлинеарности, если таковая имеется, и проведен ее анализ. При проверке на мультиколлинеарность были исключены два фактора, такие как: «Наличие проведенного интернета», «Наличие теплых полов».

Затем для проверки значимости найденных коэффициентов корреляции использовался t-критерий Стьюдента [2].

Фактическое значение этого критерия определяли по формулам

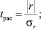
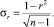(1).

Критическое значение t-статистики Стьюдента при уровне значимости 0,05 и числе степеней свободы 100: tкр ≈ 1,984.

Факторы X1, X2, X3, X4, X5, X6, X7, X8, X10, X11, X14 – признаются статистически значимыми, что свидетельствует о наличии устойчивой линейной связи между указанными факторами. Факторы же X9, X12, X13, X15, X18, X20, X21 признали статистически незначимыми и исключили их из дальнейших расчетов.

Далее провели пошаговый анализ и исключили на каждом шаге наименее связанные факторы из модели.

Шаг 1.

На первом шаге выявили, что факторы «Расположение дома», «Наличие пластиковых окон», «Наличие проведенного интернета» оказывают наименьшее влияние на стоимость квартиры, т.к. tрасч < tкр (1,984). Следовательно, следует исключить эти факторы при проведении дальнейших расчетов.

Шаг 2.

На втором шаге анализа было выявлено, что факторы «Наличие балкона», «Площадь кухни», «Этажность дома», «Наличие собственного отопления», «Состояние квартиры» оказывает наименьшее влияние на стоимость квартиры, т.к. tрасч < tкр (1,984), следовательно исключили их при проведении дальнейших расчетов.

На следующем шаге выяснили, что показатели не проходят через 0. Значение t-статистики больше табличного значения. Следовательно, факторы «Общая площадь», «Тип дома», «Количество комнат» и «Этаж» являются значимыми [3].

Таблица 1

В соответствии с полученными расчетными данными модель регрессии в линейной форме будет выглядеть следующим образом:

Y = 22669,85313 + 1930,532395·Х1 + 2799,331466·Х2 + 1685,33533·Х4 + 3365,197534·Х7.

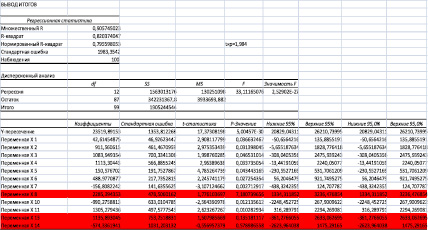
Результаты регрессионного анализа модели Y (X1, X2, X3, X4, X5, X6, X7, X8, X10, X11, X13, X14)

Для проверки значимости уравнения множественной регрессии используют F-критерий Фишера.

F-статистика. Критерий Фишера.

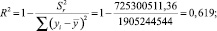
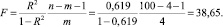
Табличное значение при степенях свободы k1 = 4 и k2 = n – m – 1 = 100 – 4 – 1 = 95, Fkp = 2,45.

Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно.

Таким образом, можно сделать вывод, что мы нашли основные ценообразующие факторы.

Метод Брандона

Отбор и анализ факторных признаков, включаемых в модель множественной регрессии для Y.

Отбор факторных признаков проводится с помощью частных коэффициентов корреляции, необходимо, чтобы коэффициент корреляции r зависимости между результирующим показателем Y и каждым j-м фактором xj должен быть отличен от нуля, и факторы x1, x2, …, xn должны быть попарно независимыми.

На Y оказывают сильное влияние –

X1 (r _{yx1/x2,х4,х7} = 0,793680915508622),

умеренное влияние –

X2 (ryx2/x1,х4,х7 = 0,630255969061171),

причем связь между

X2 и X4 (rx2x4/y,x1,х7 =–0,290562532906476)

и X2, X7 (rx2x7/y,x1,х4 =–0,3204296142673921)

слабая. Следовательно, в качестве пары факторов для построения множественной регрессии выбираем пару Х1 Х2.

• общая площадь, м2 – X1;
• тип дома – X2.

Множественная нелинейная регрессия (Y)

Для построения уравнения множественной нелинейной регрессии был использован метод Брандона.

1. Было вычислено среднее значение:

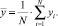
Таблица 2

Уравнения парной регрессии для YX1

2. Каждое i-е наблюдение yi было преобразовано по формуле

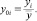
3. Для пары переменных y0i и xi1 так же, как и при парной регрессии, был выбран вид зависимости с максимальным уровнем спецификации по критерию Дарбина – Уотсона и по величине корреляционного отношения η:

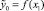[4].

Учитывая значимость коэффициентов регрессии, значимость уравнения в целом, величину корреляционного отношения и коэффициента корреляции (для линейной модели), точность аппроксимации, и отсутствие автокорреляции, в качестве модели выбираем параболическую модель второго порядка:

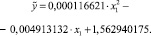
Была составлена таблица «Уравнения парной регрессии для YX2».

Учитывая значимость коэффициентов регрессии, значимость уравнения в целом, величину корреляционного отношения и коэффициента корреляции (для линейной модели), точность аппроксимации, и отсутствие автокорреляции, в качестве модели выбираем параболическую модель третьего порядка:

После определения 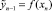строится общая формула множественной регрессии:

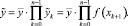
Она имеет вид:

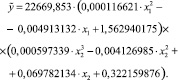
Экономическая интерпретация уравнения регрессии

Учитывая значимость коэффициентов регрессии, значимость уравнения в целом, величину корреляционного отношения, коэффициента корреляции (для линейной модели) и автокорреляцию остатков, видно, что целесообразнее выбрать параболическую зависимость. Коэффициенты нелинейной модели, построенной методом Брандона, значимы (значит, эти коэффициенты формируются под воздействием неслучайных факторов), корреляционное отношение η = 0,97549 достаточно большое (тесная связь между рассматриваемыми признаками), точность аппроксимации высокая (всего 0,55 %), автокорреляция остатков отсутствует, значит, именно эта зависимость лучше описывает исходный Y – стоимости 1 кв. метра квартиры (в руб.) [5].

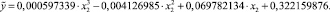
Уравнение нелинейной зависимости выглядит следующим образом:

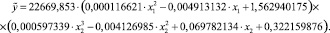
Уравнение в целом значимо, так как коэффициент детерминации очень высок R² = 0,97394, а чем больше его величина, тем больше влияние данных признаков на величину результативного. Таким образом, при повышении стоимости 1 кв. метра квартиры, стоимость общей площади возрастает, соответственно, стоимость квартиры в кирпичном доме будет дороже, чем в панельном.

Библиографическая ссылка