Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Шуленина А.В. 1 Гриняк В.М. 2

---

1 Владивостокский государственный университет экономики и сервиса

2 Дальневосточный федеральный университет

Настоящая статья посвящена вопросу применения теории нечетких множеств и нейронных сетей для оценки степени достоверности планирования закупок и продаж. В работе рассматривается модель разделения уровней достоверности в зависимости от стабильности продаж, корректности выбранного интервала и периодичности планирования закупок. Стабильность продаж выступает в данном случае как основной признак, позволяющий менеджеру принять решение о необходимости проводить планирование «вручную». В том случае, если ретроспективные продажи стабильны, возможно их автоматизированное планирование на будущие периоды. Предложена конфигурация нейро-нечёткой сети для принятия решения об уровне достоверности планирования, проведено обучение сети на реальных данных о продажах крупной торгово-закупочной организации. Статья сопровождается результатами вычислительного эксперимента, демонстрирующего работу системы.

Статья в формате PDF

0 KB

управление продажами

планирование продаж

достоверность планирования

нейро-нечёткая модель

1. Волгина О.А., Шуман Г.И., Ерохина И.В. Анализ и прогноз рынка молочной продукции в Приморском крае // Территория новых возможностей. Вестник Владивостокского государственного университета экономики и сервиса. – 2015. – № 4. – С. 41–47.

2. Гриняк В.М., Можаровский И.С., Дегтярев К.И. Нейросетевая модель планирования сезонных продаж // Информационные технологии. – 2011. – № 7. – С. 75–78.

3. Гриняк В.М., Семенов С.М. Автоматизация решения задачи классификации клиентов по стадиям взаимоотношений в современных корпоративных информационных системах // Научно-техническая информация. Сер. 2. Информационные процессы и системы. – 2008. – № 7. – С. 20–24.

4. Гриняк В.М., Семенов С.М. Модель планирования продаж в современных корпоративных информационных системах // Естественные и технические науки. – 2009. – № 1. – С. 305–312.

5. Гриняк В.М., Трофимов М.В. Мультимодельное сопровождение траектории движущихся судов с нечетким критерием детекции маневра // Территория новых возможностей. Вестник Владивостокского государственного университета экономики и сервиса. – 2011. – № 2. – С. 112–121.

6. Морозов В.О., Солодухин К.С., Чен А.Я. Нечетко-множественные методы стратегического анализа стейкхолдер-компании // Фундаментальные исследования. – 2016. – № 2–1. – С. 179–183.

7. Штовба С.Д. Проектирование нечётких систем средствами MatLab. – М.: Горячая линия телеком, 2007. – 288 с.

8. Nauk D., Klawonn F., Kruse R. Foundations of Neuro-Fuzzy Systems. – John Wiley & Sons. – 1997. – 305 c.

В условиях жесткой конкуренции для эффективной работы торгово-закупочного предприятия необходимо уделять должное внимание вопросу планирования закупок и продаж [1]. Чтобы удовлетворить спрос и не потерять клиентов, важно иметь в наличии востребованные товары, не перегружая при этом складские ёмкости. Выбор методики прогнозирования во многом зависит от стратегии, вида деятельности и масштабов предприятия.

Большинство методик планирования подразумевают ретроспективный анализ данных о продажах, то есть сбор данных за прошедшие периоды и их экстраполяцию. Самый распространенный способ прогнозирования объема продаж основан на нахождении тренда за предшествующие периоды и принятии этого значения в качестве опорного для необходимых закупок. Если дальнейшее планирование на основе тренда осуществляется полностью автоматически, то это может привести не только к перегрузке складских ёмкостей, но и к большому количеству отказов клиентам в связи с отсутствием востребованных номенклатурных позиций на складе. С другой стороны, планирование вручную (без автоматизации) при большом объёме номенклатуры может привести к чрезмерной, неоправданной нагрузке на персонал.

Ключ к решению проблемы оптимизации планирования в контексте разделения функций персонала и информационной системы лежит в определении стабильности продаж той или иной номенклатурной позиции. Автоматическое планирование с высокой степенью достоверности без участия менеджера возможно для товаров со стабильными продажами. Те же номенклатурные позиции, продажи по которым нестабильны, требуют ручной проверки и корректировки планируемых величин.

В работах [3, 4] авторами была предложена методика, которая реализует механизм экспертной оценки степени достоверности планирования закупок и продаж с цветовой интерпретацией, позволяющей проинформировать менеджера о том, для каких номенклатурных позиций автоматизированное планирование продаж достоверно, а для каких необходима «интуитивная», «ручная» корректировка полученных данных. Несмотря на то, что описанная методика позволяет решить задачу оценки достоверности планирования, необходимо отметить, что при большом объеме и разнообразии номенклатурных позиций применение указанной методики может привести к наличию в прогнозе большого количества позиций с одинаковым уровнем достоверности планирования. Это может привести к неопределенности в расстановке менеджером приоритетов для корректировки и проверке данных и, как следствие, к снижению эффективности работы сотрудника. Для оптимизации работы менеджера, который должен четко понимать, какие именно номенклатурные наименования в первую очередь требуют особого внимания при планировании, возникает необходимость формализации понятия «достоверный прогноз», с выделением различных уровней достоверности, типа: «достоверный», «недостоверный» «сомнительный» и т.п. Применение такого подхода позволит сотрудникам упорядочить свои действия, правильно определив приоритеты для корректировки и проверки данных в процессе формирования плана закупок и продаж.

Настоящая работа посвящена исследованию возможности создания информационной системы оценки степени достоверности планирования закупок и продаж с использованием идей теории нечетких систем и нейронных сетей с обучением.

Основные модельные представления задачи

В работах [3, 4] рассматривается модель изменения значения объёма продаж X во времени, которая может быть выражена формулой

Xq = G(q) + η(q),

где G(q) – функция, выражающая детерминированный закон эволюции величины X (тренд) в зависимости от момента времени с номером q; η(q) – случайная величина, характеризующая отклонение фактического значения показателя от его тренда (здесь и далее будем считать, что η(q) – некоррелированная случайная величина с нулевым математическим ожиданием).

Оценки среднего значения и среднеквадратичного отклонения показателя X могут быть выражены следующим образом:

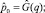
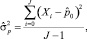
где J – количество моментов времени, участвующих в оценке.

Достоверность экстраполяции показателя X оценивается дискретным набором значений на основании истинности трёх условий:

1. Величины Xi лежат близко к своему среднему значению, то есть для всех i:

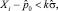(1)

где k – заданный параметр ширины доверительного интервала.

2. Экстраполируемые значения Xi с большой степенью достоверности не равны 0:

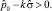(2)

3. Для всех i, то есть среди Xi не встречаются нулевые значения:

Xi > 0. (3)

Данные условия проверяются для каждой позиции номенклатуры, а затем принимается решение о достоверности планирования по совокупности значений условий.

Дискретная оценка уровня достоверности планирования продаж позволяет привлечь внимание менеджера в первую очередь к проверке наиболее недостоверных планируемых величин. Вместе с тем при большом разнообразии номенклатурных позиций может оказаться слишком много товаров с одинаковым уровнем достоверности планирования, что не позволит сотруднику адекватно оценить ситуацию. В этом случае становится актуальной задача представления уровня достоверности непрерывной величиной. Здесь рационально использовать идеи, положенные в основу задач систем нечеткой логики. Аналогичный подход реализован и успешно применяется во многих других отраслях деятельности, не только в экономике [6, 2], но и технике, например при оценке опасности движения судов [5].

Фаззификация задачи

Для решения поставленной задачи – перехода от дискретной оценки достоверности к непрерывной целесообразно использовать нейро-нечёткую сеть. На вход этой сети подаются три лингвистические переменные, характеризующие стабильность продаж, корректность выбранного интервала и периодичности, с термами «большое» и «малое».

Пусть 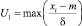– оцененная величина стабильности продаж (1). Введем лингвистическую переменную P1 «оценка величины U1» с термами «большое» и «малое» и функциями принадлежности типа «дополнение», определёнными на универсальном множестве U1 ∈ [0, 3]:

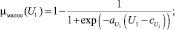
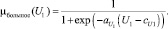
Терм «малое» соответствует ситуации, когда экстраполируемые значения не выходят за границы доверительного интервала, близки к своему среднему значению, и это означает, что продажи можно считать стабильными. Терм «большое» говорит о том, что продажи нестабильны и могут носить сезонный характер.

Пусть 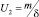– оцененная корректность длины выбранного интервала (2). Введем лингвистическую переменную P2 «оценка величины U2» с термами «большое» и «малое» и функциями принадлежности типа «дополнение», определёнными на универсальном множестве U2 ∈ [0, 3]:

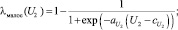
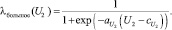
В данном случае терм «малое» говорит о том, что данных для планирования недостаточно, терм «большое» – что в планируемый период продажи по выбранной номенклатурной позиции будут иметь место.

Пусть 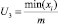– оцененная корректность выбранной периодичности (3). Введем лингвистическую переменную P3 «оценка величины U3» с термами «большое» и «малое» и функциями принадлежности типа «дополнение», определёнными на универсальном множестве U3 ∈ [0, 2]:

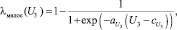
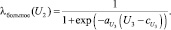
Терм «малое» означает, что периодичность анализа данных выбрана неправильно. В частности, если продажи некоторой номенклатурной позиции имеют место лишь раз в месяц, то не имеет смысла принимать период для расчетов и прогнозирования равным неделе. Терм «большое» соответствует корректно выбранной периодичности планирования.

Величины P1, P2 и P3 (вход) обрабатываются нейро-нечеткой сетью, показанной на рис. 1, на выходе которой формируется числовое значение u ∈ [0, 3] – степень достоверности планирования закупок и продаж; значение u = 0 соответствует наименьшей степени достоверности, u = 3 – наибольшей. Сеть состоит из пяти слоёв [8] (рис. 1).

В узлах первого слоя μ1, μ2, λ1, λ2, ν1, ν2 вычисляются значения функция принадлежности μмалое, μбольшое, λмалое, λбольшое, νмалое, νбольшое соответственно. Узлы П второго слоя (всего 8 узлов) соответствуют посылкам 8 возможных нечетких правил, комбинирующих все возможные значения величин P1, P2 и P3 (табл. 1).

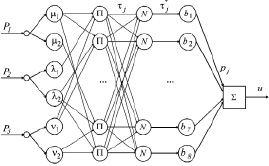
Рис. 1. Схема нейро-нечеткой сети, определяющей степень достоверности планирования закупок и продаж

Таблица 1

Система нечетких правил

Каждый узел второго слоя соединен с теми узлами первого слоя, которые формируют посылки соответствующего правила. Выходом каждого узла второго слоя является степень выполнения j-го правила τj, которая рассчитывается как произведение входных сигналов. Узлы N третьего слоя рассчитывают относительную степень выполнения каждого нечеткого правила по формуле

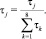
Узлы b1, b2, ..., b8 четвертого слоя формируют заключения нечетких правил; фактически bj – это значения выхода сети при однозначном выполнении только j-го правила. Каждый узел соединен с одним узлом третьего слоя и рассчитывает вклад одного нечеткого правила в выход сети по формуле pj = bjτj.

Единственный узел пятого слоя агрегирует результат, полученный по разным правилам, суммируя вклады всех правил

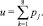
Обучение нейро-нечеткой сети (рис. 1) состоит в настройке параметров функций принадлежности 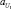, , 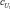, , 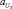, 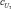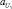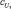и коэффициентов b1, b2, ..., b8 узлов четвертого слоя. Обучение может быть проведено с применением различных методов. В данном случае обучение проводилось на обучающей выборке с экспертным формированием заключений нечетких правил. Коэффициенты bj назначались экспертом, а параметры функций принадлежности определялись настройкой системы на обучающей выборке.

Обучающая выборка формируется следующим образом. Моделируется решение задачи с оценкой условий (1), (2) и (3) для различных номенклатурных позиций. При «недостоверном» прогнозе u = 0 необходимо ручное планирование, если u = 1, то прогноз «сомнителен» и требуется проверка планируемых величин. В том случае, если прогноз имеет минимальную погрешность, то есть является «убедительным» u = 2 (при этом проверка значений производится на усмотрение менеджера и является необязательной). Если же прогноз является «достоверным» u = 3, то план закупок не требует проверки. Накапливая данные о продажах различных товаров за разные периоды, формируют общую обучающую выборку «вход-выход», на базе которой обучают сеть (рис. 1), пользуясь известными методами обучения сетей такого типа [7, 8].

Результаты математического моделирования

Численное моделирование рассматриваемой задачи проводилось в системе MATLAB [7]. Обучающая выборка формировалась на реальных данных о продажах крупной торгово-закупочной организации по продаже автозапчастей за 12 месяцев с периодичностью 2 месяца по 700 номенклатурным позициям.

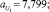
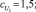
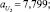
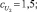
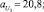
Были заданы следующие значения параметров функций принадлежности μмалое(P1), μбольшое(P1), λмалое(P2), λбольшое(P2), νмалое(P3), νбольшое(P3): 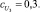В данном случае начальные параметры функций принадлежности задавались экспертом, далее система подверглась обучению и настройке.

Обучение системы проводилось при следующих значениях параметров bj, соответствующих 8 возможным нечетким правилам: b1, b2, b3, b4 = 0; b5 = 1; b6, b7 = 2; b8 = 3. Ошибка после настройки сети составила 0,111.

В результате после настройки и обучения гибридной нейро-нечеткой сети были получены значения непрерывной оценки степени достоверности планирования (табл. 2).

Таблица 2

Дискретная и непрерывная оценки степени достоверности планирования

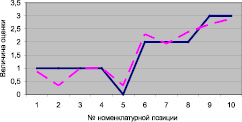
Рис. 2. Дискретная и непрерывная величина оценки степени достоверности (сплошная – дискретная величина, пунктир – непрерывная)

Сравнивая дискретные и непрерывную величину оценки, можно видеть, что для многих номенклатурных позиций с одинаковой дискретной оценкой непрерывная величина отличается в среднем в пределах до 0,5 (рис. 2), что позволит автоматизированной системе, основанной на данной сети, автоматически ранжировать прогноз в рамках одного уровня достоверности.

Результаты моделирования подтверждают ожидаемый эффект разделения уровней достоверности в зависимости от стабильности продаж, корректности выбранного интервала и периодичности планирования. Предложенная модель нейро-нечеткой системы может быть успешно применена на практике для оценки степени достоверности планирования закупок и продаж.

Библиографическая ссылка