Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Халафян А.А. 1 Кошкаров А.А. 1 Пелипенко Е.Ю. 1

---

1 ФГБОУ ВО «Кубанский государственный университет»

В статье предложен метод построения рейтинга вузов, основанный на анализе сходства между ними как точками метрического многомерного пространства, если известны числовые значения показателей эффективности. Сходство (различие) вузов определяется посредством расстояний между ними, по принципу – чем меньше расстояние, тем больше сходство. Для составления рейтинга вузов предлагается использовать эталонный вуз, аккумулирующий наилучшие свойства сравниваемых вузов. Рейтинг совпадает с рангом при упорядочивании вузов по степени близости к гипотетическому эталонному вузу. Метод прост в реализации, так как основан на использовании стандартных процедур статистических пакетов. Возможна его полная автоматизация посредством макросов используемых модулей. За счет стандартизации показателей позволяет оценивать эффективность объектов произвольной природы, в том числе и структурных подразделений вузов, по количественным показателям, измеренным в различных шкалах и с различными единицами измерений. Как пример построен рейтинг университетов Южного федерального округа по эффективности деятельности за 2015 год.

Статья в формате PDF

0 KB

эффективность

вузы

критерий

объект

рейтинг

ранжирование

сходство

расстояние

классификационный анализ

1. Антипина И.О. Механизмы независимой оценки качества образования // Инновационные проекты и программы в образовании. – 2015. – Т. 4. – С. 12–16.

2. Борисов В.А. Методический подход к оценке деятельности медицинских учреждений регионального здравоохранения на основе формирования компьютерной информационной системы / В.А. Борисов, Г.В. Попова // Системный анализ и управление в биомедицинских системах. – 2016. – Т. 15. – № 1. – С. 183–190.

3. Информационно-аналитические материалы по результатам проведения мониторинга эффективности образовательных организаций высшего образования [Электронный ресурс]. – Режим доступа: http://indicators.miccedu.ru/monitoring/ (15.04.2016).

4. Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ. – М.: Высшая школа, 1989. – 367 с.

5. Халафян А.А. STATISTICA 6. Статистический анализ данных. – М.: Бином, 2010. – 528 с.

6. Халафян А.А. Компьютерный анализ данных как инструментарий в спортивной аналитике / А.А. Халафян, Т.В. Бущуева, А.Г. Минасян // Физическая культура, спорт – наука и практика. – Краснодар, 2016. – № 2. – С. 52–57.

7. Черненький А.В. Принципы оценки и ранжирования структурных подразделений вуза // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета. – 2016. – № 116. – С. 1327–1339.

8. Черноруцкий И.Г. Методы принятия решений. – СПб.: БХВ-Петербург, 2005. – 416 с.

В настоящее время стала актуальной проблема оценки эффективности учреждений – медицинских организаций, вузов, школ и т.д. c последующим составлением их рейтинга [1, 2, 7]. Следуя словам Галилея «измеряй все, поддающееся измерению, и сделай таким все, не поддающееся измерению», разрабатываются критерии по оценке эффективности не только самих вузов, но и структурных подразделений – факультетов, кафедр, а также их сотрудников. Не будем касаться методики выбора критериев оценки эффективности – над этой важной проблемой работает достаточно большое количество специалистов. Ограничимся исследованием другой, не менее значимой проблемы ранжирования объектов «измерения» в соответствии со значениями совокупности показателей, характеризующих их качество.

Краткий обзор методов

Пусть заданы m объектов О1, О2, …, Оm и совокупность n количественных показателей Q1, Q2, …, Qn, определяющих их качественные характеристики, которые назовем критериями. Значение j-го критерия, соответствующее i-му объекту, обозначим как qij, 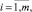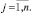Критерии Qj обладают тем свойством, что если объект Оk предпочтительнее объекта Оl (Оk f Оl), то qkj > (или <) qlj, где f знак предпочтения. Знак > используем в том случае, если предпочтению соответствует большее значение критерия, знак <, если предпочтению соответствует меньшее значение критерия. Требуется ранжировать объекты по степени предпочтения относительно всех критериев Qj, 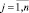, что по сути эквивалентно составлению их рейтинга.

Данная задача на вид проста, но зачастую сложен метод её решения, так как он зависит от характера и количества как объектов Оi, так и от характера и количества критериев Qj. На практике редки случаи, в которых объекты Оi оцениваются одним критерием, что даст возможность их ранжирования простым сравнением (упорядочиванием) значений критерия. Наиболее вероятен случай, когда критериев несколько и объекты будут несравнимыми, образуя так называемое множество Парето, когда один объект лучше других по одному критерию, но хуже по другим. Рассмотрим наиболее известные подходы к решению этой «многокритериальной» задачи.

1. Сведение к «однокритериальной» задаче. Вводится так называемый интегральный критерий Qs, который представляет собой скалярную функцию от критериев Qj, 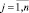[4]:

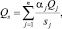(1)

где aj – веса, которые отражают относительный вклад частных критериев Qj в интегральный критерий; sj – коэффициент, позволяющий перейти к безразмерным величинам от Qj. При этом, так как критериям соответствуют различные характеры предпочтения, весу aj присваивается знак (+), если предпочтению соответствует максимальное значение критерия, и знак (–) в противном случае.

Тогда «многокритериальная» задача ранжирования сводится к «однокритериальной» задаче – упорядочиванию (ранжированию) объектов в соответствии со значениями интегрального критерия по принципу – чем больше значение интегрального критерия Qs, тем предпочтительнее объект:

Оk f Оl, если Qs(Оk) > Qs(Оl),

а значит, и выше его место (рейтинг).

К сожалению, данный способ имеет один существенный недостаток – не формализована процедура выбора весовых коэффициентов. Веса выбираются экспертом «потолочным» методом, поэтому их значения весьма субъективны. Учитывая, что при этом интегральный критерий Qs очень чувствителен к изменению весов, велика вероятность получения ошибочного решения задачи. К данному подходу можно отнести и широко известные методы Саати и Коггера и Ю, также предполагающие нахождение весовых коэффициентов [6].

2. Из всех критериев Q1, Q2, …, Qn выбирается основной, или главный, критерий Qосн и далее используется как интегральный критерий Qs. Естественно, такое упрощение значительно облегчит вычислительные процедуры, но можно ли будет считать полученный результат решением задачи, или в какой-то степени близким к нему? Наверняка в большинстве случаев ответ будет отрицательным. Данный подход может иметь место только в том случае, если выбранный критерий значительно доминирует по важности над остальными и по значимости превосходит их все вместе взятые.

3. Зачастую, чтобы избежать необходимости оптимизации интегрального критерия (1), как аддитивной функции слагаемых, имеющих различные размерности, критерии Qi переводят в балльную шкалу и далее переходят к простому суммированию (вычитанию) баллов, т.е. интегральный критерий Qs представляет собою измерение в балльной шкале. Предпочтительнее будет тот объект, которому соответствует наибольшее количество баллов. Но и такой подход не лишен принципиальных недостатков – переход от более сильных количественных шкал (интервальной, отношений) к балльной, являющейся более слабой порядковой шкалой, сопровождается большой потерей информации о свойствах объектов, что в итоге приведет к неверному решению задачи. К тому же, если придерживаться определенной математической строгости, операция суммирования в порядковых шкалах не определена.

Метрический подход

Ранжирование объектов (составление их рейтинга) предполагает их сравнение. Рассмотрим метод сравнения, если известны числовые значения критериев, характеризующих качество объектов, основанный на их представлении как точек n-мерного пространства и определении сходства (различия) между ними посредством расстояний метрических пространств.

Представим значения критериев qij, 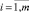; 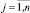в виде таблицы (матрицы) с числом строк, равным количеству объектов m, и количеством столбцов, равным n:

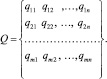(2)

Строки матрицы соответствуют объектам Oi, столбцы – критериям Qj. Такое представление позволяет нам рассматривать объекты Oi как точки (векторы) многомерного пространства в системе координат Q1, Q2, …, Qn, с координатами qi1, qi2, …, qin и оценивать расстояние между ними при помощи одной из метрик, реализованных в модуле Кластерный анализ пакета STATISTICA [5], в частности посредством евклидова расстояния:

dе(Oi, Oj) = (Σк (qiк – qjк)2)1/2. (3)

Для возможности ранжирования объектов введем в рассмотрение гипотетически наилучший объект (эталонный) и обозначим его 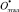. Определяя минимальные или максимальные значения по столбцам, в зависимости от характера предпочтения соответствующего критерия найдем наилучшие значения каждого критерия, которые и будут координатами 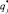(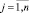) вектора ,

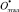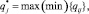
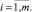(4)

Вычисляя парные расстояния между объектами О1, О2, …, Om, 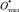, мы легко можем оценить сходство не только между ними, но и ранжировать их по расстоянию до эталонного объекта 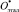по принципу – чем меньше расстояние, тем выше рейтинг.

Так как расстояние (3) вычисляется по исходным данным, на его значения могут сильно влиять различия между единицами измерения осей. Поэтому при вычислении расстояний по одной из приведенных формул данные следует привести к безразмерному виду нормированием (стандартизацией) столбцов матрицы Q.

Если обозначить через 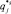, 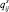– стандартизованные значения, то расстояние ρi между объектами Оi и 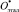легко вычислить по формуле

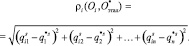(5)

Чтобы составить рейтинги объектов, достаточно вычисленные расстояния упорядочить в порядке возрастания и поставить в соответствие каждому значению ρi, а значит, и каждому объекту Оi ранги 1, 2, …, m. Объект с рангом 1 и будет наилучшим, так как ему соответствует минимальное расстояние.

Практическая реализация метода

Как пример, определим рейтинги университетов Южного федерального округа (ЮФО) по эффективности их деятельности. Из рассмотрения исключены медицинские университеты, так как целесообразно сравнивать однородные по структуре вузы.

Значения критериев эффективности университетов взяты из информационно-аналитических материалов по результатам проведения мониторинга 2015 года деятельности образовательной организации высшего образования [3]. Представлены следующие критерии: образовательная деятельность (ОД, бал.); научно-исследовательская деятельность (НИД, тыс. руб.),; международная деятельность (МД, %); финансово-экономическая деятельность (ФЭД, тыс. руб.); заработная плата профессорско-преподавательского состава (ЗП ППС, %); трудоустройство (ТР, %); дополнительный показатель (ДП).

В табл. 1 представлены значения критериев Адыгейского государственного университета (АГУ); Астраханского государственного технического университета (АсГТУ); Астраханского государственного университета (АсГУ); Волгоградского государственного социально-педагогического университета (ВГСПУ); Волгоградского государственного архитектурно-строительного университета (ВолгГАСУ); Волгоградского государственного аграрного университета (ВолгГАУ); Волгоградского государственного технического университета (ВолгГТУ); Волгоградского государственного университета (ВолгГУ); Калмыцкого государственного университета (КГУ); Кубанского государственного университета физической культуры, спорта и туризма (КГУФКСТ); Кубанского государственного аграрного университета (КубГАУ); Кубанского государственного технологического университета (КубГТУ); Кубанского государственного университета (КубГУ); Южного федерального университета (ЮФУ); Южно-Российского государственного политехнического университета им. М.И. Платова (ЮРГПУ).

В первой строке приведены пороговые значения (ПЗ) критериев.

Естественно, не представляет сложности оценка рейтинга вузов отдельно по каждому критерию – достаточно упорядочить их по значениям критериев, например по возрастанию, и поставить им в соответствие номера 1, 2, 3, …, 15. Решим более сложную задачу – при помощи процедур кластерного анализа, реализованных в среде пакета STATISTICA, определим рейтинги университетов, по совокупности заданных значений критериев эффективности.

Таблица 1

Значения критериев для университетов

В последней строке таблицы отображены значения критериев для гипотетического, несуществующего эталонного вуза (ЭВ), который аккумулировал наилучшие значения критериев по всем вузам. Так как предпочтению университетов соответствуют большие значения всех представленных в таблице критериев, то значения критериев для ЭВ представляют собою наибольшие значения столбцов таблицы, которые выделены полужирным курсивом. Из таблицы видно, что наибольшие значения ОД и ЗП ППС у ЮФУ; наибольшее значение НИД у ВолгГТУ; наибольшие значения МД и ТР у КубГТУ; наибольшее значение ФЭД у АГУ, наибольшее значение ДП у КГУФКСТ. Так как критерии – величины разного порядка и размерности, например ДП - безразмерная величина, принимающая значения не более 10, а ФЭД исчисляется в тыс. руб. и принимает значения от 1000 до 3000, столбцы таблицы были стандартизованы (нормированы).

При помощи процедуры Иерархическая классификация модуля Кластерный анализ по стандартизованным данным были вычислены парные, евклидовы расстояния между вузами, как точками многомерного (размерности 7) пространства, которые представлены в табл. 2.

Таблица симметричная, в ячейках на главной диагонали расположены расстояния между одноименными вузами, поэтому равны 0. Чем меньше расстояние, тем выше сходство между вузами по совокупности 7 критериев. Так, наибольшее сходство между двумя волгоградскими вузами ВолгГАСУ и ВолгГАУ – расстояние минимальное, равное 1,09. Наибольшее различие между КубГАУ и АГУ, расстояние максимальное, равное 5,34.

Места университетов в построенном рейтинге – полезная, но из-за «бедности» порядковой шкалы достаточно однобокая информация, так как установлен лишь порядок между ними. В то же время матрица расстояний может предоставить более полную информацию о структуре сходства и различия между объектами.

Наиболее известный метод представления матрицы расстояний при иерархической кластеризации основан на идее дендрограммы, или диаграммы дерева, которая представляет графическое изображение результатов процесса последовательной кластеризации. Из дендрограммы на рис. 1, построенной методом полной связи, следует, что изначально группу однородности (кластер) образуют 2 вуза – ВолгГАСУ и ВолгГАУ – расстояние между ними чуть более 1. При незначительном увеличении расстояния группу однородности образуют уже АсГУ и АсГТУ, расстояние между ними чуть более 1,2. При расстоянии 1,35 самостоятельный кластер образуют КубГАУ и ВолгГУ. Дальнейшее увеличение расстояния ведет к последовательному присоединению к образованным кластерам других университетов, что в итоге приводит к образованию большой группы однородности – кластера 2. Аналогичным образом группу однородности – кластер 1 образуют университеты – ВолгГТУ, ЮФУ, КубГУ и ЭВ. Интересным является кластер 3, который состоит только из двух университетов – АГУ и КГУФКСТ.

Таблица 2

Евклидовы расстояния между вузами

Продолжение табл. 2

Дендрограмма иллюстрирует структурную схему сходства между объектами. Несколько другого характера информацию можно получить при помощи метода многомерного шкалирования, который позволяет объекты n-мерного пространства перенести в пространство меньшей размерности, в частности на плоскость, сохранив порядок расстояний между ними, т.е. объекты, близкие в многомерном пространстве, близки и в пространстве меньшей размерности. По-сути речь идет об изображении на плоскости пространственного расположения объектов. На диаграмме, построенной методом многомерного шкалирования (рис. 2), видно, что университеты из одного кластера локализованы в определенной части плоскости. Наиболее близко к ЭВ расположен ЮФУ, несколько дальше – ВолгГТУ, далее – КубГУ, которые в совокупности образуют кластер 1. У этих вузов наиболее высокие рейтинги. Университеты, образующие кластер 2, локализованы в левой, противоположной ЭВ части диаграммы, на небольшом удалении друг от друга, им соответствуют средние и низкие рейтинги. На достаточном отдалении от остальных университетов находится АГУ, образующий кластер 2 с КГУФКСТ.

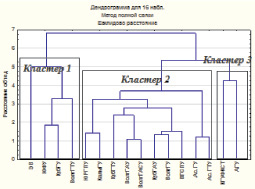
Рис. 1. Дендрограмма классификации вузов

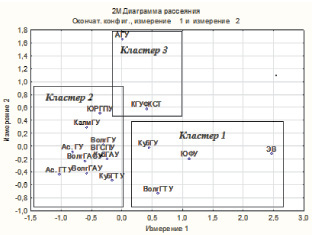
Рис. 2. Дендрограмма рассеяния в системе координат, измерение 1, 2

Расстояние между объектами можно рассматривать как интегральный количественный критерий, характеризующий качество объектов сравнения. Его достоинство в том, что он принимает преимущественно различные значения при сравнении объектов. Если среди объектов будет обнаружен объект, аккумулирующий наилучшие свойства других, то его и следует рассматривать как эталонный.

Недостаток интегрального критерия в том, что его значения зависят от состава объектов. Устранить этот недостаток можно, если ввести предельные, недостижимые объектами значения критериев, обозначив их критериями качества эталонного объекта. Тогда можно было бы ввести в рассмотрение коэффициент эффективности вузов, как величину, обратную расстоянию [6]. К сожалению, пороговые значения, приведенные в первой строке табл. 1, на самом деле не оправдывая свое название и являясь, по-видимому, номинальными значениями, не могут быть использованы в качестве предельных значений, так как в большинстве случаев они меньше значений показателей университетов.

Заключение

Таким образом, предложенный метод составления рейтинга объектов произвольной природы позволяет исследовать структуру их сходства при помощи процедур иерархической классификации и многомерного шкалирования. Используя расстояния до эталонного объекта с заданными предельными значениями показателей, возможно построение более информативного интегрального количественного критерия как величины обратной расстоянию. Метод прост в реализации, так как основан на использовании стандартных процедур статистических пакетов. Возможна его полная автоматизация посредством макросов используемых модулей, позволяет оценивать эффективность объектов произвольной природы, в том числе и структурных подразделений вузов – факультетов, кафедр. Метод не требует использования весовых коэффициентов, обладающих высокой степенью субъективности. Как пример при помощи рассмотренного метода составлены рейтинги университетов Южного федерального округа по эффективности их деятельности.

Библиографическая ссылка