Переход на стандарты нового поколения взаимосвязан с заметным возрастанием роли самостоятельной работы студентов, что требует не только улучшения материально-технического обеспечения в сфере профессионального образования, но и учебно-методического сопровождения этой работы. В существенной мере эта проблема затрагивает дисциплины, относившиеся ранее к циклу общепрофессиональных дисциплин. В частности, по всем направлениям инженерной подготовки предусмотрено освоение основ электротехники. Однако изданные в последние несколько лет учебники, например [1, 3, 4], рассчитаны на использование для ограниченного числа направлений подготовки бакалавров и магистров, где эти дисциплины формируют в основном профессиональные компетенции. В статье приведены основные результаты разработки электронной версии пособия для изучения закономерностей в RL-цепях переменного тока студентами любых инженерных направлений.
Результаты исследования и их обсуждение
В первой части пособия приведены основные теоретические соотношения для последовательной RL-цепи, подключаемой к источнику гармонического сигнала. С использованием временных и векторных диаграмм проанализировано изменение фазовых соотношений сигналов в этой цепи.
Для усвоения закономерностей в такой цепи на уровне понимания разработана программа в среде MS Visual Studio [2, 5], что обусловлено возможностью быстрой разработки приложений. Эта программа обеспечивает выполнение необходимых расчетов по схеме с задаваемыми параметрами элементов цепи и источника сигнала (на основе имеющихся в первой части пособия теоретических соотношений) и построение совмещенных временных зависимостей совокупности параметров RL-цепи.
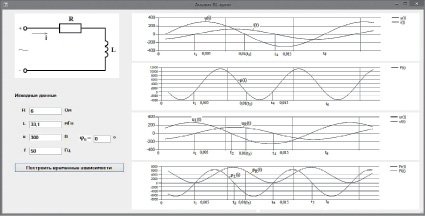
Демонстрационный график совмещенных временных зависимостей
Демонстрационный график совмещенных временных зависимостей, показанный на рисунке, получен по разработанной программе для цепи с параметрами: R = 6 Ом; L = 33,1 мГн; u = 300sin ωt В; f = 50 Гц.
Из первого (верхнего) графика на рисунке видно, что при нулевой начальной фазе φu = 0 входного напряжения u(t) начальная фаза тока φi (φi = 60°), полученная при расчете, соответствует установленной ранее закономерности:
φ = φu – φi = 0 – (–60°) = 60°.
Это значение φ принадлежит диапазону от 0 до 90°.
На втором графике (нумерация графиков в направлении сверху вниз) показана временная зависимость мгновенной мощности RL-цепи, подключенной к источнику синусоидального напряжения. За период Т входного напряжения u(t) (от t0 = 0 до t6) мгновенная мощность p(t) имеет две положительные полуволны (от t1 до t3 и от t4 до t6) и две отрицательные полуволны (от t0 до t1 и от t3 до t4), т.е. мгновенная мощность изменяется во времени с удвоенной частотой (относительно частоты входного напряжения).
Интервал от t1 до t3 определяет положительное значение мгновенной мощности p(t), т.к. на этом интервале (см. первый график) положительное значение имеет и входное напряжение u(t), и ток i(t). То есть источник энергии работает в режиме генератора. Поступающая от источника энергия частично накапливается в магнитном поле катушки индуктивности, а частично преобразуется в тепловую энергию в резистивном элементе с последующей диссипацией (рассеянием) в окружающее пространство.
На интервале от t3 до t4 напряжение u(t) на входе RL-цепи становится отрицательным (см. первый график), а ток i(t) в цепи остается положительным. Произведение этих величин в любой момент времени t на интервале от t3 до t4 (исключая t = t3 и t = t4) дает отрицательное значение мгновенной мощности p(t). Это означает, что на интервале от t3 до t4 источник энергии на входе работает в режиме потребления энергии: накопленная в магнитном поле катушки индуктивности энергия частично возвращается в источник энергии. Такому режиму соответствует участок на интервале от t3 до t4 на графике p(t). При этом не вся энергия, накопленная в магнитном поле катушки индуктивности (накопленная к моменту времени t3), возвращается в источник энергии. Часть этой энергии преобразуется в резисторе R в тепловую энергию с последующей диссипацией в окружающую среду. После момента времени t4 и до конца первого периода (до момента времени t6) напряжение u(t) и ток i(t) отрицательны (см. первый график). Произведение двух отрицательных величин дает положительную величину: мгновенная мощность p(t) на участке от t4 до t6 положительна, т.е. источник энергии на входе вторично (за первый период) переходит в генераторный режим. В этом режиме идет процесс повторного накопления энергии в магнитном поле катушки индуктивности, сопровождающийся частичным преобразованием генерируемой электрической энергии (генерируемой источником напряжения на входе цепи) в тепловую энергию в резисторе R.
На третьем графике изображены временные зависимости падений напряжения на резисторе uR(t) и на катушке индуктивности uL(t). Сигнал uR(t) совпадает по фазе с током i(t): на участке от t1 до t4 оба сигнала имеют положительную полуволну, а на других участках (в пределах рассматриваемого периода) оба сигнала отрицательны и имеют одинаковые тенденции изменения во времени.
Сигнал uL(t) относительно сигнала uR(t) (как и относительно сигнала i(t)) имеет временной сдвиг, соответствующий опережению по фазе на  . Например, в момент времени t1, когда напряжение uR(t) проходит через нулевое значение из отрицательной области в положительную, сигнал uL(t) достигнет максимума, а в последующий промежуток времени начинает уменьшаться. Сигнал uR(t) достигнет такого состояния только к моменту времени t2 (отстоящему от t1 на промежуток времени, соответствующий 1/4 периода или 90°), т.е. по фазе uL(t) опережает uR(t) на
. Например, в момент времени t1, когда напряжение uR(t) проходит через нулевое значение из отрицательной области в положительную, сигнал uL(t) достигнет максимума, а в последующий промежуток времени начинает уменьшаться. Сигнал uR(t) достигнет такого состояния только к моменту времени t2 (отстоящему от t1 на промежуток времени, соответствующий 1/4 периода или 90°), т.е. по фазе uL(t) опережает uR(t) на  .
.
На нижнем (четвертом) графике представлены временные зависимости мгновенных мощностей для резистора pR(t) и для катушки индуктивности pL(t). Для любого момента времени t применительно к pR(t) можно записать, что
pR(tj) ≥ 0.
Последнее соотношение обусловлено тем, что i(t) и uR(t) совпадают по фазе и во времени изменяются синхронно. В момент времени t1 и t4 (где обе величины обращаются в нуль) значение pR(t) равно нулю, а при любом другом значении tj, pR(tj) > 0, т.к. представляет собой либо произведение положительных величин i(t) и uR(t) (на участке между t1 и t4), либо произведения отрицательных величин i(t) и uR(t) в течение первого периода входного напряжения, интервал от t1 до t4. Мгновенная мощность pR(t) изменяется с удвоенной частотой (относительно частоты входящего напряжения). Действительно, за половину периода (см. интервал от t0 до t3 на верхнем и нижнем графиках) сигнал pR(t) в момент t3 возвращается в такое же состояние, которое он имел в t0.
Сигнал pL(t) тоже изменяется с удвоенной частотой относительно частоты входящего напряжения. За полупериод входного напряжения (см. интервал от t0 до t3 на верхнем графике) сигнал pL(t) к моменту времени t3 возвращается в такое же состояние, которое он имел в t0 (см. нижний график).
За второй полупериод входного напряжения (интервал от t3 до t6, на верхнем графике) сигнал pL(t) в момент времени t6 вторично возвращается в такое же состояние, которое он имел в t0 (см. нижний график).
Но в отличие от pR(t) сигнал pL(t) имеет участок с отрицательным значением. На нижнем графике первая положительная полуволна pL(t) (участок от t1 до t2) равна отрицательной полуволне (участок от t2 до t4). Вторая положительная полуволна pL(t) (участок от t4 до t5) равна первой. Отрицательные участки pL(t) на интервале от t0 до t1 и от t5 до t6 в сумме составляют еще одну отрицательную полуволну.
В целом за период входного напряжения сумма положительных участков pL(t) равна сумме отрицательных участков pL(t). Это свидетельствует о том, что в идеализированной катушке индуктивности не происходит непосредственного преобразования электрической энергии. Запасаемая в магнитном поле катушки индуктивности электрическая энергия (на положительных участках pL(t) полностью возвращается в электрическую цепь на отрицательных участках pL(t)). Возвращаемая электрическая энергия частично преобразуется в тепловую энергию в резистивном элементе, а некоторая часть этой электрической энергии (возвращаемая из магнитного поля катушки индуктивности) реально возвращается в источник энергии на входе цепи (когда этот источник действует в цепи в режиме потребителя).
На первом графике показано, что в момент времени t4 мгновенное значение тока i(t4) равно нулю, напряжение на входе цепи u(t4) отрицательно и сохраняет тенденцию к убыванию. Мгновенная мощность RL-цепи p(t4) равна нулю (см. второй график), т.к. один из сомножителей, определяющих эту величину, равен нулю. Напряжение на резисторе (совпадающее по фазе с током в RL-цепи) uR(t4) тоже равно нулю (см. третий график). Соответственно, равна нулю и мгновенная мощность pR(t4) на резисторе R (см. нижний график). Отлично от нуля в момент времени t4 напряжение uL(t4) на катушке индуктивности: оно достигает минимального значения (uL(t4) = uL(t)min). Это обусловлено тем, что момент времени t4 соответствует максимальной скорости изменения тока i(t). На верхнем графике точка i(t4) – это точка перегиба, в которой изменяется направление протекания тока. Поэтому в катушке индуктивности формируется максимальное значение эдс самоиндукции 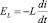 , а по модулю uL(t4) = EL(t4). Так как uR(t4) = 0, то напряжение на входе цепи в этот момент времени равно напряжению на катушке индуктивности: u(t4) = uL(t4) (см. первый и третий графики). Мгновенное значение мощности pL(t4) тоже равно нулю (нижний график): хотя значение uL(t4) экстремально, но ток в RL-цепи i(t4) равен нулю.
, а по модулю uL(t4) = EL(t4). Так как uR(t4) = 0, то напряжение на входе цепи в этот момент времени равно напряжению на катушке индуктивности: u(t4) = uL(t4) (см. первый и третий графики). Мгновенное значение мощности pL(t4) тоже равно нулю (нижний график): хотя значение uL(t4) экстремально, но ток в RL-цепи i(t4) равен нулю.
Обобщая анализ RL-цепи для момента времени t4, можно отметить, что в момент равенства нулю тока в этой цепи отсутствует как генерируемая мощность, так и потребляемая: p(t4) = pR(t4) = pL(t4) = 0.
Для момента времени t3 напряжение на входе RL-цепи равно нулю (см. первый график), равно нулю и значение мгновенной мощности цепи p(t3). Но здесь это относится только к результирующей мощности RL-цепи. Следует учитывать, что i(t3) > 0 (см. первый график). При положительном значении тока в RL-цепи напряжение uL(t3) на катушке индуктивности отрицательно (см. третий график). Соответственно, отрицательное значение имеет мгновенная мощность pL(t3) на катушке индуктивности. То есть, в момент времени t3 катушка индуктивности возвращает в цепь энергию, накопленную ранее в магнитном поле катушки индуктивности. Так как мгновенная мощность pL(t3) = 0, то мощность катушки индуктивности в момент времени t3 равна по модулю мгновенной мощности pR(t3), потребляемой резистором. В рассматриваемый момент времени энергия, отдаваемая катушкой индуктивности, полностью трансформируется в тепловую энергию резистивного элемента. Действительно, uR(t3) > 0 и мгновенная мощность pR(t3) > 0, а по модулю (см. на нижнем графике) pR(t3) = pL(t3).
На интервале от t3 до t4 (см. второй график) мощность RL-цепи отрицательна, т.е. обеспечивается возврат части энергии источнику входного напряжения от магнитного поля катушки индуктивности. Если исключить дискретные моменты времени t3 и t4 (pR(t3) = pL(t3), а pR(t4) = pL(t4) = 0), то для любого момента tj в диапазоне t3 < tj < t4 по модулю pL(tj) > pR(tj) (см. нижний график). На этом временном интервале разность числовых значений мгновенных мощностей pL(tj) и pR(tj) определяет мгновенное значение мощности p(tj), возвращаемой входному источнику напряжения. После момента времени t3 разность числовых значений pL(tj) и pR(tj) растет (до 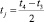 ), а затем уменьшается (см. эту закономерность на нижнем графике). Поэтому возвращаемая входному источнику напряжения мгновенная мощность p(tj) до середины участка между t3 и t4 растет, а затем уменьшается (см. второй график).
), а затем уменьшается (см. эту закономерность на нижнем графике). Поэтому возвращаемая входному источнику напряжения мгновенная мощность p(tj) до середины участка между t3 и t4 растет, а затем уменьшается (см. второй график).
Для временных диаграмм на рис. 1 необходимо одно уточнение. По умолчанию было предположено, что расчетная RL-цепь в исходном состоянии разомкнута и на элементах R и L отсутствуют напряжения (так называемые нулевые начальные условия). Замыкание ключа осуществляют мгновенно в момент времени t = 0. По результатам теоретического расчета для принятых параметров RL-цепи на промежутке времени от t0 до t1 должен происходить частичный возврат энергии от катушки индуктивности к входному источнику напряжения. Но в момент t0 в магнитном поле катушки индуктивности энергия еще не накоплена (процесс накопления начнется только после момента времени t1).
Выводы
Изменяя исходные параметры, можно получать информацию обо всех параметрах цепи, выявляя, например, закономерности, связанные с перераспределением энергии, генерируемой источником сигнала. Высокий уровень наглядности способствует углубленному пониманию закономерностей в цепи RL. Параллельно идет процесс формирования исследовательских навыков. Использование программы обеспечивает индивидуализацию задания на самостоятельную работу. Разработка может быть включена в комплект материалов по формированию соответствующего учебно-методического комплекса.
Библиографическая ссылка
Арванова М.М., Георгиева М.А., Бабич А.Е. РАЗРАБОТКА ЭЛЕКТРОННОЙ ВЕРСИИ ПОСОБИЯ ДЛЯ ИЗУЧЕНИЯ ЗАКОНОМЕРНОСТЕЙ В RL-ЦЕПИ ПЕРЕМЕННОГО ТОКА // Фундаментальные исследования. 2016. № 5-1. С. 9-12;URL: https://fundamental-research.ru/ru/article/view?id=40240 (дата обращения: 01.02.2026).



