Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Адамадзиев К.Р. 1 Адамадзиева А.К. 1

---

1 ФГБОУ ВО «Дагестанский государственный университет»

Целью исследования является построение моделей, характеризующих зависимости между ключевыми экономическими показателями регионов по данным за разные временные периоды и оценка их характеристик. Для достижения поставленной цели решены следующие задачи: сформулировано исходное информационное обеспечение; разработан алгоритм и выполнены расчеты, связанные с определением параметров моделей и их статистических характеристик; сформирован комплекс взаимосвязанных таблиц с результатами и проведен их анализ. Для решения перечисленных задач собрана, обобщена и организована в виде таблиц исходная информация, в качестве которой выступают статистические данные по четырем ключевым показателям регионов России: валовому региональному продукту (Y), стоимости основных фондов (K), численности занятых в экономике (L) и объемам инвестиций (I) за три временных периодов – 2005, 2010 и 2014 гг.

Статья в формате PDF

0 KB

производственная функция

экономический показатель

регион

группировка

совокупность объектов

стохастические связи и зависимости

регрессия

временной период

анализ

метод

модель

1. Адамадзиев К.Р., Адамадзиева А.К. Компьютерное моделирование в экономике: учебное пособие. – Махачкала: Издательско-полиграфический центр ДГУ, 2014. – 211 с.

2. Ковалев В.В. Финансовый анализ: методы и процедуры. – М.: Финансы и статистика, 2005. – 560 с.

3. Мельник М.В., Поздеев В.Л. Теория экономического анализа: учебник для магистров. – М.: Изд-во Юрайт, 2014. – 261 с.

4. Розанов Г.В., Френкель Л.А. Корреляционный и регрессионный анализ в экономических исследованиях // Экономика и математические методы. – 1967. т. III, вып. 3.

5. Эконометрика: учебник / под ред. И.И. Елисеевой. – 2-e изд., перераб. и доп. – М.: Финансы и статистика. – 2005. – 576 с.

Выявление и оценка связей и зависимостей в экономике приобрели в наше время исключительно важную роль при принятии управленческих решений любым экономическим объектом. Связей и зависимостей в экономике много и их принято классифицировать по различным признакам. В частности, по признаку детерминированности различают два типа связей: функциональные и стохастические. Связь называется функциональной (или жестко детерминированной), если любому значению факторного признака соответствует вполне определенное неслучайное значение признака результативного. Связь называется стохастической (вероятностной), если любому значению факторного признака соответствует множество значений признака результатного [1, 2, 3, 4, 5].

Функциональные связи и зависимости в экономике достаточно широко изучены, выявлены, описаны и широко применяются в экономической практике. Процессы выявления и оценки стохастических связей и особенно их практическое применение лишь только начинаются. Настоящее исследование посвящено выявлению и анализу стохастических связей и зависимостей.

Среди стохастических связей и зависимостей любого экономического объекта особое место занимают связи (зависимости) между ключевыми показателями в абсолютном выражении и рассчитываемыми на их основе относительными показателями. На уровне экономики регионов к абсолютным показателям можно отнести: валовой региональный продукт (Y), стоимость основных фондов (K), численность занятых в экономике (L), объем инвестиций (I). На их основе можно рассчитать ряд относительных показателей, в частности следующие: фондоотдачу (fo), производительность труда (y), инвестициоотдачу (io), фондовооруженность труда (k), инвестициовооруженность труда (u), коэффициент обновления основных фондов (Ko).

Между перечисленными показателями экономики регионов могут существовать как парные, так и многофакторные стохастические связи. В частности, наши исследования показали наличие следующих взаимосвязей:

а) парных: Y от K; Y от L; Y от I; K от I; I от Y; y от k; y от u;

б) двухфакторных: Y от K, L; Y от L, I.

В силу ограниченности объема в настоящем исследовании рассматриваются полученные результаты лишь для четырех зависимостей: Y от K, L; Y от L, I; y от k; y от u.

Связи (зависимости) между объемами продукции и объемами затрат на ее производство в экономике получили название «производственных функций». Таковыми в нашем случае являются зависимости Y от K, L; Y от L, I. Расчеты и анализ проведены для четырех совокупностей данных: для всех регионов страны, а также для трех групп регионов (малых, средних и крупных). Деление регионов на группы осуществлено по показателю «валовой региональный продукт».

Для каждой группы регионов и в целом по всем регионам за каждый год построены по два уравнения регрессии для производственных функций (линейного и степенного видов). Эти два вида уравнений имеют преимущества перед остальными, главное из которых состоит в возможности экономического истолкования параметров. Наши расчеты и анализ их результатов показал также, что исследуемые зависимости производительности труда от фондо- и инвестициовооруженности труда более адекватно описываются уравнениями регрессии линейного и степенного видов.

Построить уравнение регрессии означает, во-первых, рассчитать параметры и провести их анализ; во-вторых, рассчитать статистические характеристики и с их помощью оценить приемлемость построенных уравнений; в-третьих, определить на основе построенных уравнений ряд дополнительных (производных) показателей, провести их анализ и сформулировать выводы, представляющие научный и практический интерес.

Сущность, методы и алгоритмы для расчета параметров и статистических характеристик уравнений регрессии и другие вопросы теории и практики их построения и применения можно найти в учебной литературе по эконометрике и научных публикациях. Кроме того, в настоящее время имеются инструментальные средства, позволяющие рассчитывать как в отдельности, так и одновременно параметры уравнений регрессии, и целый ряд статистических характеристик. К ним можно отнести в первую очередь процедуру «Мастер функций» из MS Excel [см., например, 1, 4, 5].

Поэтому перейдем непосредственно к рассмотрению полученных нами результатов, сначала для уравнений линейного, а затем степенного видов.

В уравнениях линейного вида параметр b может принимать значения: b ≠ 0, b = 0. Значение параметра b существенно влияет на исследуемую зависимость. Поэтому целесообразно построение и анализ этих зависимостей как при b ≠ 0, так и b = 0.

В табл. 1 приведены величины параметров уравнений для двухфакторных производственных функций линейного вида для зависимостей Y от K, L и Y от L, I по трем группам регионов и по всем регионам в целом при b ≠ 0.

Анализ данных табл. 1 позволяет сформулировать ряд выводов:

– во-первых, по данным за 2005 г. параметр m1 по группам регионов от малых до крупных увеличивался, т.е. предельная эффективность основных фондов росла; предельная эффективность использования трудовых ресурсов в малых регионах оказалась положительной, а в средних и крупных – отрицательной, отрицательность предельной эффективности свидетельствует об избытке этого ресурса и необходимости сокращения его объемов; кроме того, в 2010 и в 2014 гг. предельная эффективность использования основных фондов и трудовых ресурсов была положительной и росла вместе с ростом размеров регионов (исключение составило использование основных фондов в 2010 г., в котором эффективность фондов по малым регионам оказалась выше, чем по средним);

– во-вторых, в соответствии с параметрами зависимости Y от L, I: эффективность использования трудовых ресурсов (m2) по группам регионов в 2005 г. снизилась, в 2014 г. имело место уменьшение – рост; эффективность использования инвестиций (m3) менялась по схеме уменьшение – рост в 2005 г., рост – уменьшение в 2010 и рост в 2014 г.; изменение m2 в динамике по рассматриваемым периодам: по малым, средним и по всем регионам имел место рост, по крупным – рост – уменьшение; изменение m3 в динамике: по малым регионам – уменьшение, по средним – рост, по крупным и по всем регионам – уменьшение – рост.

Проведенный нами анализ статистических характеристик, рассчитываемых для функций линейного вида, показал, что все уравнения, параметры которых приведены в табл. 1, являются приемлемыми (проверялись индекс детерминации, стандартная ошибка для зависимого показателя, F-критерий Фишера, t-критерий Стьюдента, средняя ошибка аппроксимации).

Таблица 1

Величины параметров уравнений производственных функций линейного вида, выражающих зависимость ВРП (Y) от стоимости основных фондов (K), численности занятых в экономике (L) и объема инвестиций (I), рассчитанные по данным групп регионов России за 2005, 2010 и 2014 гг.

В уравнениях линейного вида для производственных функций, параметры которых приведены в табл. 1, параметр b принять неравным нулю (b ≠ 0). При b = 0 двухфакторные линейные уравнения для рассматриваемых производственных функций будут иметь вид

Y = m1·K + m2·L; Y = m2·L + m3·I.

Если обе части каждого из этих уравнений разделить на L, то получим следующие уравнения:

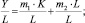
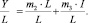
Значимость этих уравнений состоит в том, что их можно преобразовать в уравнения, выражающие зависимость производительности труда от фондовооруженности и от инвестициовооруженности труда:

y = m1·k + m2; y = m2 + m3u,

где y = Y/L – производительность труда; k = K/L – фондовооружённость труда; u = I/L – инвестициовооружённость труда.

Таким образом, уравнения производственных функций линейного вида при b = 0 позволяют, во-первых, оценить параметры и статистические характеристики самих этих уравнений, во-вторых, построить новые уравнения, показывающие зависимость одного из главных показателей эффективности экономики (т.е. производительности труда) от каждого из двух главных показателей технического уровня экономики (т.е. от фондовооружённости труда и инвестициовооружённости труда).

Математическая запись уравнений регрессии линейного вида, выражающих зависимости производительности труда (y) от фондовооружённости труда (k) и инвестициовооружённости труда (u), построенных по данным регионов России за 2005, 2010 и 2014 гг. приведена в табл. 2.

По табл. 2 можно сформулировать ряд выводов, в частности следующие:

а) параметры уравнений для зависимости y от k показывают рост производительности труда (в тыс. руб.) при увеличении фондовооружённости труда на 1 тыс. руб. в 2005 г. по группе средних регионов предельная эффективность, характеризуемая параметром при переменной, была чуть выше, чем по малым регионам, а по крупным – в 1,5 раза превышала ее величины для малых и средних регионов. В 2014 г. по малым регионам предельная эффективность выросла на 10 % по сравнению с 2005 г., по средним – уменьшилась почти в 1,5 раза, по крупным также имеет место уменьшение;

Таблица 2

Математическая запись уравнений линейного вида, выражающих зависимости производительности труда (y) от фондовооружённости труда (k) и инвестицио-вооружённости труда (u), построенных по данным регионов России за 2005, 2010 и 2014 гг.

б) по уравнениям для зависимости производительности труда (y) от инвестициовооружённости труда (u) можно утверждать, что за три рассматриваемых в таблице периода предельная эффективность показателя-фактора (u) по группе средних регионов оказалась заметно ниже, чем по группе малых; в 2014 г. по сравнению с 2005 по малым и средним регионам предельная эффективность показателя-фактора (u) выросла (по средним регионам более чем в 2 раза), по крупным – она уменьшилась, но была выше, чем по малым и средним;

в) в целом по всем регионам в 2014 г. по сравнению с 2005 г. произошли следующие изменения: предельная эффективность по фондовооружённости труда уменьшилась с 0,3379 до 0,3114 тыс. руб., а предельная эффективность по инвестициовооружённости труда увеличилась с 1,2931 до 2,4628 тыс. руб., т.е. почти в 2 раза.

Свои особенности и ценность имеют уравнения регрессии для производственных функций степенного вида.

Как известно, в случае степенной зависимости параметр (b) экономического смысла не имеет, но параметры при переменных (т.е. показатели степеней) всегда имеют экономический смысл. Это обусловлено тем, что параметры в степенных уравнениях равны показателям, называемым коэффициентами эластичности 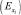) и рассчитываемыми по формуле

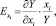
где 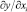– предельная эффективность i-го показателя-фактора; xi – величина i-го показателя-фактора.

В случае степенной зависимости коэффициенты эластичности представляют собой числовые величины, т.е. 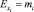, а для всех других видов уравнений регрессии 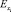является переменной величиной, выражаемой вышеприведенной формулой.

В табл. 3 приведены величины параметров уравнений регрессии, построенных нами производственных функций степенного вида для обеих зависимостей (Y от K, L и Y от L, I).

В уравнениях производственных функций степенного вида показатели степеней (коэффициенты эластичности) можно складывать (m1 + m2 и m2 + m3). При этом суммарные величины представляют собой величины роста результативного показателя в процентах при одновременном увеличении на 1 % обоих ресурсов, входящих в уравнение. Полученная сумма может быть больше, меньше или равна единице. Если сумма коэффициентов эластичности больше единицы, то говорят об эффекте масштаба, если меньше единицы, то об отсутствии эффекта масштаба.

Таблица 3

Величины параметров уравнений производственных функций степенного вида, выражающих зависимость ВРП (Y) от стоимости основных фондов (K), численности занятых в экономике (L) и объема инвестиций (I), рассчитанные по данным групп регионов России за 2005, 2010 и 2014 гг.

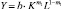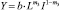Особое место занимает случай, когда m1 + m2 = 1 (m2 + m3 = 1). В этом случае параметр m2 = 1 – m1 (m2 = 1 – m3), т.е. уравнения производственных функций упрощаются и примут вид и . Анализ величин m1 + m2 и m2 + m3 из табл. 3 показывает отсутствие эффекта масштаба по обоим видам зависимостей (Y от K, L и Y от L, I) во всех трех группах регионов за все три рассматриваемых временных периода. Но такой эффект имеет место в целом по всем регионам во всех рассматриваемых уравнениях производственных функций. При этом по уравнениям обоих зависимостей Y от K, L и Y от L, I эффект масштаба оказался в 2005 г. максимальным, а в 2010 г. минимальным.

По данным табл. 3 сформулируем ряд выводов:

а) величины коэффициентов эластичности для зависимости Y и K, L показывают, что: во-первых, прирост производительности труда от увеличения стоимости основных фондов значительно выше, чем от увеличения численности работников; во-вторых, эластичность фондов повышается с ростом размеров регионов, а эластичность труда уменьшается; в-третьих, в 2014 г. по сравнению с 2005 г. коэффициенты эластичности основных фондов для всех групп регионов значительно снизились, а коэффициенты эластичности труда – выросли;

б) по уравнению зависимости Y от K, L эластичность труда по малым и средним регионам ниже, чем по крупным, и ниже, чем эластичность инвестиций; коэффициенты эластичности труда в 2014 г. по сравнению с 2005 г. по малым и средним регионам выросли, а по крупным – уменьшились;

в) в целом по всем регионам России эластичность основных фондов и инвестиций в 2014 г. по сравнению с 2005 г. уменьшилась, а эластичность труда – увеличилась.

Анализ статистических характеристик, рассчитанных для всех построенных уравнений регрессии степенного вида для производственных функций, показывает, что: во-первых, все построенные уравнения являются приемлемыми; во-вторых, по приемлемости уравнения степенного вида существенно превосходят уравнения линейного вида. В частности по величине средней ошибки аппроксимации все уравнения степенного вида можно оценить на «хорошо», т.е. эти ошибки менее 10 %.

Выше нами было показано, что уравнения производственных функций линейного вида при b = 0 можно преобразовать в уравнения, выражающие зависимость производительности труда (y, тыс. руб.) от фондовооружённости труда (k, тыс. руб.) и от инвестициивооружённости (u, тыс. руб.).

Что-то подобное, но несколько иначе можно сделать в случае степенной зависимости. Если в уравнениях регрессии степенного вида, выражающих зависимость производительности труда от фондо- и инвестициивооружённости

y = b·k^m и y = b·u^m,

где y, k, u выразить в виде y = Y/L; k = K/L; u = I/L и подставить эти значения в оба уравнения для производительности труда, то они преобразуются в уравнения производственных функций

Y = b·K^mL ^1–m и Y = b·I^mL ^1–m.

Можно действовать и наоборот: во-первых, предположить, что ml + m2 = l (m2 + m3 = l); во-вторых, разделить обе части уравнений на величину L, т.е.

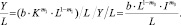
Откуда 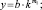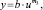где y = Y/L – производительность труда, тыс. руб. k = K/L – фондовооруженность труда, тыс.руб.; u = I/L – инвестициовооруженность труда, тыс.руб.

Математическая запись уравнений степенного вида, выражающих зависимость производительности труда от фондо- и инвестициовооруженности труда, полученных нами по данным регионов страны за 2005, 2010 и 2014 гг., приведена в табл. 4.

Главным аналитическим показателем в табл. 4 является коэффициент эластичности (или показатель степени) в уравнениях степенного вида, т.е. численное значение параметров для фондо- и инвестициовооруженности труда (ml, mЗ).

По данным табл. 4 сформулируем несколько выводов:

а) коэффициенты эластичности для фондовооруженнности труда: по данным за 2005 г. максимальным оказался для группы средних регионов, минимальным – для малых; за 2010 и 2014 гг. – максимальными для крупных регионов и минимальными для средних; коэффициенты эластичности для инвестициовооруженности труда: в 2005 г. максимальным был по группе малых регионов, минимальным – по группе крупных; в 2010 и 2014 гг. – наоборот, минимальным – по малым регионам, максимальным – по крупным;

б) по группам регионов в динамике по трем рассматриваемым временным периодам коэффициенты эластичности по фондам: по группе малых регионов – уменьшились; по группе средних – в 2010 г. по сравнению с 2005 г. почти в 2 раза уменьшились, в 2014 г. – незначительно выросли; по крупным регионам в 2010 г. имело место незначительный рост, в 2014 г. – уменьшение; в динамике изменения коэффициентов эластичности по инвестициовооруженности труда по группе малых регионов в 2010 г. имело место уменьшение, в 2014 г. – рост; по средним и крупным – рост в оба периода;

Таблица 4

Математическая запись уравнений степенного вида, выражающих зависимости производительности труда (y) от фондовооружённости труда (k) и инвестицио-вооружённости труда (u), построенных по данным регионов России за 2005 и 2014 гг.

в) величины коэффициентов эластичности по фондовооруженности труда для совокупности всех регионов в динамике росли, а по инвестициовооруженности труда – уменьшались.

Библиографическая ссылка