Исследование характера поведения стальных фиброволокон в матрице бетона имеет целью построение общей модели поведения сталефибробетона при сложных видах нагружения как в упругой стадии, так и в стадии трещинообразования; причём в последнем случае особое значение приобретают данные о работе единичной фибры при его смещении в бетоне-матрице. Существующие математические модели работы железобетонных конструкций можно разделить на две группы: методы, основанные на рассмотрении напряжённо-деформированного состояния сечения, и методы, не использующие деформационные зависимости. К первой группе относят метод расчёта элементов по нормальным сечениям, построенный на единых принципах (гипотеза плоских сечений, диаграммы, учитывающие нелинейный характер деформирования материалов) [1]. Такой подход позволяет с единых позиций вести расчёт по прочности, образованию и раскрытию трещин, по деформациям. Настоящая работа посвящена совершенствованию такого метода. Суть метода поясняется на рис. 1, где показана стадия образования трещины в центральном сечении изгибаемого элемента (балки из СФБ) при чистом изгибе. Поперечное сечение балки разбивается на множество прямоугольных секций, в каждой из которых с ростом кривизны происходят процессы сжатия (в случае, если секция расположена выше нейтральной линии) или растяжения, а также образование трещин, рост которых сдерживается работой стальных фибр.
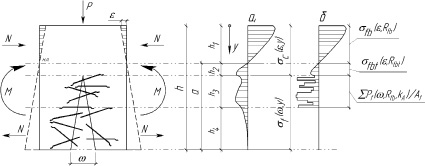
Рис. 1. Распределение нормальных напряжений в сечении изгибаемого элемента из СФБ
Реакция поперечного сечения может быть определена здесь посредством итеративного подхода. Для каждого секционного элемента поперечного сечения на высоте y кривизна на каждом шаге постепенно увеличивается, при этом положение нейтральной оси определяется путём решения уравнений равновесия [5]:
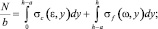 (1)
(1)
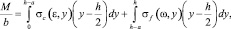 (2)
(2)
где N – продольные усилия в сечении балки; M – изгибающий момент; b – ширина балки; h – высота сечения балки; y – координата секции сечения балки, в котором рассчитывается нормальное напряжение; σс(ε, y) – нормальные напряжения сжатия и растяжения секции сечения СФБ-элемента на высоте y; σf(ω, y) – нормальные напряжения, возникающие в результате работы фибры в трещине центрального сечения СФБ-элемента на высоте y; ε – относительные деформации в секции сечения; ω – ширина раскрытия трещины (рис. 1, а).
Распределение нормальных напряжений носит нелинейный характер. Условно эпюру нормальных напряжений в сечении можно разбить на четыре участка: h1 – участок, на котором действуют сжимающие напряжения; h2 – участок, где растягивающие напряжения распределяются на целостный композитный материал – сталефибробетон: они включают растягивающие напряжения самого бетона и касательные напряжения, действующие на поверхности соприкосновения фибры и бетона; h3 – участок, на котором растягивающие напряжения работают на выход фибры из матрицы бетона, а также, если фибра располагается под непрямым углом к сечению балки, – на скол бетона при изгибе и деформации фибр; h4 – высота «абсолютной» трещины, где нет работы фибры и бетона. Для расчёта напряжений на участках h3 и h4 существуют различные модели [5, 6, 7]. В таких моделях предполагается, что работа отдельных волокон секции может быть просуммирована с целью получения суммарного вклада фибр в пределах одной секции в общую эпюру напряжений. Такие модели с высокой достоверностью позволяют определять напряжение, создаваемое фибрами в трещинах, в случае использования прочных бетонов-матриц, а также малых геометрических размеров фибр. Шлакобетон относится к лёгким мелкозернистым бетонам с классом по прочности В10…В30. Для таких бетонов более приемлемы модели, заключающиеся в дифференцированном рассмотрении единичных фибр (разнонаправленных, с различной глубиной заделки) в отдельной секции сечения, а затем суммировании действующих на них сил, определяемых из диаграмм «нагрузка - смещение» («P-δ»), далее относя их к площади поперечного сечения фибр (рис. 1, б):
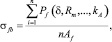 (3)
(3)
где n – количество фибр в отдельной секции.
Такие диаграммы характеризуют работу фибры в шлакобетоне. На практике диаграммы удобно представлять в виде кривой, проходящей через ряд характеристических точек, координаты которых зависят от прочностных характеристик бетона, геометрических характеристик фибры и определяются эмпирически; значения координат для шлакобетона представлены в работе [2].
В центральном сечении изгибаемого элемента взаимовлияние стальных фибр будет сказываться на характере диаграмм их работы. Наличие соседних фибр будет разрушать бетон, окружающий центральную фибру, соответственно, уменьшая её работу по смещению из бетона-матрицы, т.е. понижением ординат характеристических точек. Целью настоящего исследования является изучение характера такого понижения, получение коэффициента (kA), характеризующего изменение величины вклада в работу элемента фиброволокна в зависимости от длины заделки соседних фибр и качества сцепления между ними.
В проведённых исследованиях в качестве волокна использовалась фибра «Драмикс» бельгийской фирмы «Бекарт», длиной lf = 60 мм, диаметром df = 0,8 мм, с временным сопротивлением разрыву Rf = 980–1200 МПа. Геометрические характеристики фибры и образца приведены в [2]. Опытные образцы и схемы анкеровки фибры в образцах представлены на рис. 2. В таблице представлены значения длин заделки фибр для каждого типа образцов и углы ориентации крайних фибр (меньший угол наклона к плоскости действия продольных сил) для каждой комбинации. Угол ориентации фибры принимается положительным в случае, если фибра удаляется от центральной в матрице бетона, в противном случае угол ориентации фибры принимается отрицательным. Расстояние между фибрами в образце составляло 5 мм (максимальный размер фракции отсева от дробления литого шлакового щебня). В исследованиях использовались бетоны классов В7,5 (Rm = 8,6 МПа), В15 (Rm = 18,3 МПа), В20 (Rm = 22,1 МПа), В25 М (Rm = 27,6 МПа). Всего было проведено 240 отдельных испытаний, – по два опытных образца на каждый вариант комбинации анкеровки и класса шлакобетона.
Испытания проводились в специально разработанном устройстве, позволяющем определять смещение фибры при выходе из бетона-матрицы [3].
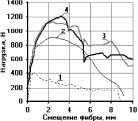
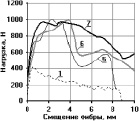
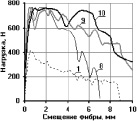
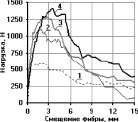
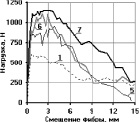
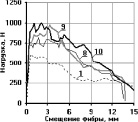
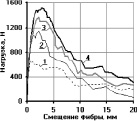
На рис. 3 представлены усреднённые эмпирические кривые зависимости «P-δ» для трёх серий испытаний: класс бетона – В25 (Rm = 27,6 МПа), цифрами обозначены графики, соответствующие комбинациям анкеровок фибр, представленным в таблице.
Анализ полученных экспериментальных диаграмм для фибр, заделанных в комбинациях 2–10, позволяет сделать вывод об их взаимовлиянии на анкерующую способность в мелкозернистом шлакобетоне. Соседние фибры оказывают влияние на работу центральной фибры. Работа единичной фибры известна – это площадь, ограниченная осями координат и кривой диаграммы «P-δ» (комбинации 1). Вычисление работы центральной фибры в случае комбинаций 2–10 осуществляется посредством разделения общей работы комбинации фибр на работу каждой фибры в отдельности. Сравнивая полученную работу центральной фибры с работой единичной фибры с той же длиной заделки, получим коэффициент изменения работы kA.

а

б

в
Рис. 2. Опытные образцы: а – длин заделки центральной фибры lf,an = 10 мм; б – lf,an = 20 мм; в – lf,an = 30 мм
Значения длин заделок фибр для каждой серии испытаний
|
Номер серии |
Номер комбинации заделок фибр |
Длина заделки центральной фибры lf,an, мм |
Среднее значение длин заделок соседних фибр |
|
Ориентация соседних фибр, град. |
|
|
φ1 |
φ2 |
|||||
|
1 |
1 |
10 |
0 |
0 |
– |
– |
|
2 |
10 |
1,0 |
0 |
0 |
||
|
3 |
20 |
2,0 |
0 |
0 |
||
|
4 |
30 |
3,0 |
0 |
0 |
||
|
5 |
10 |
1,0 |
30 |
30 |
||
|
6 |
20 |
2,0 |
25 |
25 |
||
|
7 |
30 |
3,0 |
20 |
20 |
||
|
8 |
10 |
1,0 |
–30 |
–30 |
||
|
9 |
20 |
2,0 |
–25 |
–25 |
||
|
10 |
30 |
3,0 |
–20 |
–20 |
||
|
2 |
1 |
20 |
0 |
0 |
– |
– |
|
2 |
10 |
0,5 |
0 |
0 |
||
|
3 |
20 |
1,0 |
0 |
0 |
||
|
4 |
30 |
1,5 |
0 |
0 |
||
|
5 |
10 |
0,5 |
30 |
30 |
||
|
6 |
20 |
1,0 |
25 |
25 |
||
|
7 |
30 |
1,5 |
20 |
20 |
||
|
8 |
10 |
0,5 |
–30 |
–30 |
||
|
9 |
20 |
1,0 |
–25 |
–25 |
||
|
10 |
30 |
1,5 |
–20 |
–20 |
||
|
3 |
1 |
30 |
0 |
0 |
– |
– |
|
2 |
10 |
0,33 |
0 |
0 |
||
|
3 |
20 |
0,67 |
0 |
0 |
||
|
4 |
30 |
1,0 |
0 |
0 |
||
|
5 |
10 |
0,33 |
30 |
30 |
||
|
6 |
20 |
0,67 |
25 |
25 |
||
|
7 |
30 |
1,0 |
20 |
20 |
||
|
8 |
10 |
0,33 |
–30 |
–30 |
||
|
9 |
20 |
0,67 |
–25 |
–25 |
||
|
10 |
30 |
1,0 |
–20 |
–20 |
||
По результатам обработки опытных данных предложена формула для определения коэффициента kA, характеризующего изменение величины вклада в работу элемента фибровой арматуры в зависимости от средней длины заделки соседних фибр в шлакобетоне, их ориентации по отношению к центральной фибре и прочности шлакобетона-матрицы:
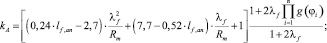
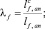
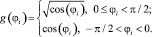 (4)
(4)
Здесь Rm – прочность шлакобетона на сжатие; n – количество фибр в радиусе 5 мм от центральной.
На рис. 4 графически представлен пример области значения коэффициента kA для шлакобетона класса В25 и φ1 = 0, φ2 = 0. Кривая 1 здесь построена по формуле (4) для фибр с длиной заделки lf,an = 10 мм, 2 – для фибр с lf,an = 20 мм и 3 – для фибр с lf,an = 30 мм; точками обозначены эмпирические значения коэффициента.
а
б


в
Рис. 3. Усреднённые эмпирические кривые зависимости «P-δ» загруженных концов фибр, заделанных в шлакобетон класса В25: а – для 1-ой серии испытаний, б – для 2-й серии; в – для 3-й серии; цифрами обозначены номера комбинаций заделок фибр
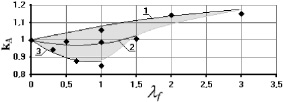
Рис. 4. Область значений коэффициента kA для шлакобетона класса В25 и φ1 = 0, φ2 = 0
Из формулы (4) видно, что коэффициент стремится к единице в случае роста значения прочности Rm шлакобетона-матрицы, т.е. взаимовлияние фибр в бетоне высокого класса минимизируется, поскольку при смещении фибра в таком бетоне деформируется, не разрушая бетон. Ориентация фибры под углом φ ≠ 0 значительно уменьшает коэффициент kA, поскольку такие фибры в большей степени способствуют образованию микротрещин в бетоне, особенно в области поверхности образца, где фибра изгибается, появляются сколы. Заметим, что для одних и тех же значений величины lf возможны случаи увеличения работы центральной фибры (kA > 1), а также случаи уменьшения её работы (kA < 1).
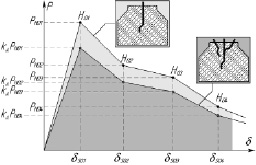
Рис. 5. Влияние коэффициента kA на изменение ординат характеристических точек кусочно-линейной диаграммы «P-δ»
В случае использования кусочно-линейных диаграмм коэффициент kA определяет, во сколько раз увеличится (уменьшится) площадь под кусочно-линейной диаграммой. При этом влияние данного коэффициента на ординаты характеристических точек диаграммы зависит от величины lf, т.е. от взаимного расположения центральной и соседних фибр. Заметим, что при изменении ординат характеристических точек кусочно-линейной диаграммы «P-δ» общее изменение площади фигуры, ограниченной линиями диаграммы, произойдёт в kA раз (рис. 5).
Результаты исследований могут являться универсальными, если использовать формулы приведения ориентированной фибры к фибре, направленной параллельно оси действия нормальных сил в трещине фибробетона [2, 4]. Центральная фибра в этом случае может быть также ориентирована под ненулевым углом к плоскости поверхности трещины, что позволяет рассчитывать напряжения, возникающие в центральной трещине изгибаемых СФШБ-элементов, производя расчёты по соответствующим алгоритмам и диаграммным методикам на ЭВМ.
Библиографическая ссылка
Корнеев А.М., Бузина О.П., Суханов А.В., Шипулин И.А. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ВЗАИМОВЛИЯНИЯ СТАЛЬНЫХ ФИБР В СЕЧЕНИИ ИЗГИБАЕМОГО ЭЛЕМЕНТА ИЗ СТАЛЕФИБРОШЛАКОБЕТОНА // Фундаментальные исследования. 2016. № 4-3. С. 506-511;URL: https://fundamental-research.ru/ru/article/view?id=40206 (дата обращения: 15.02.2026).




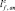 , мм
, мм