Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кононова С.А. 1 Победаш П.Н. 2 Харитонов А.В. 3

---

1 ФГБОУ ВО «Кемеровский государственный университет»

2 ФГБОУ ВО «РЭУ им. Г.В. Плеханова» Кемеровский филиал

3 ФГБНУ «Сибирский научно-исследовательский институт экономики сельского хозяйства»

В статье на примере сельскохозяйственного предприятия (свинокомплекса, производящего два вида продукции – мясо в живом весе и мясо в убойном весе) предлагается сбалансированная система показателей (ССП), позволяющая выявить факторы и условия достижения итоговых результатов. Указанная ССП базируется на математической модели управления деятельностью указанного предприятия, описываемой в форме статической задачи линейного программирования. При этом ставится задача определения такого числа работников свинофермы и убойного пункта (входящих в состав свинокомплекса), при котором максимизируется статический аналог чистой приведенной стоимости производственного проекта по выпуску мясной продукции. Представленная модель учитывает составляющие ССП и может быть обобщена на случай более чем двух типов производимой продукции и произвольного вида деятельности предприятия.

Статья в формате PDF

0 KB

сбалансированная система показателей

математическая модель управления деятельностью предприятия

1. Бондарева Г.С. Совершенствование продовольственного обеспечения населения региона (на материалах Кемеровской области): дис. ... канд. экон. наук. – Новосибирск. 2013. – 183 с.

2. Бондарева Г.С., Медведев А.В., Косинский П.Д. Оценка эффективности функционирования агропродовольственного кластера региона // Фундаментальные исследования. – 2013. – № 11(2). – С. 261–265.

3. Горбунов М.А. Оптимизационный пакет прикладных программ «Карма» и его применение в задачах бизнес-планирования / М.А. Горбунов, А.В. Медведев, П.Н. Победаш, А.В. Смольянинов // Фундаментальные исследования. – 2015. – № 4. – С. 42–47.

4. Каплан Р., Нортон Д. Организация, ориентированная на стратегию. Как в новой бизнес-среде преуспевают организации, применяющие сбалансированную систему показателей. – М.: Олимп-Бизнес, 2009. – 392 с.

5. Косинский П.Д., Бондарев Н.С., Бондарева Г.С. Продовольственное обеспечение региона: вопросы теории и практики / под науч. ред. д-ра экон. наук, академика РАН П.М. Першукевича: ГНУ СибНИИЭСХ Рос. акад. с.-х. наук. – Новосибирск, 2015. –397 с.

6. Косинский П.Д., Бондарев Н.С., Бондарева Г.С. Совершенствование налоговых отношений в агропродовольственном кластере региона // Региональная экономика: теория и практика. – 2013. – № 5(284). – С. 22–29.

7. Косинский П.Д., Меркурьев В.В., Чупрякова А.Г. Формирование агломераций муниципальных образований: теоретические и прикладные аспекты; под ред. П.Д. Косинского. – Томск: Изд-во Том. ун-та, 2015. – 206 с.

8. Косинский П.Д., Медведев А.В., Меркурьев В.В., Победаш П.Н. Математическое моделирование агломерации муниципальных образований // Фундаментальные исследования. – 2013. – № 8(6). – С. 1446–1449.

9. Медведев А.В., Косинский П.Д., Бондарева Г.С. Экономико-математическое моделирование агропродовольственного кластера региона // Фундаментальные исследования. – 2013. – № 10(10). – С. 2203–2206.

10. Победаш П.Н. Поддержка принятия решений при оценке эффективности инвестиционных проектов развития экономических систем // Перспективы развития информационных технологий. – 2013. – № 11. – С. 42–47.

11. Федулова Е.А. Разработка, реализация и оценка инвестиционной стратегии в системе публичного управления экономическим развитием территории / под общ. ред. Н.В. Фадейкиной. – Новосибирск: САФБД, 2014. – 399 с.

Сбалансированная система показателей (ССП) представляет собой инструмент управления хозяйствующим субъектом на основе оценки его эффективности по набору показателей, отражающих существенные аспекты его деятельности с позиции реализации стратегии. Сбалансированность системы показателей означает, что:

1) ее составляющие логически связаны и дают комплексное представление об экономическом субъекте;

2) такая система показателей позволяет учитывать взаимодействие как материальных, так и нематериальных активов, таких как способность удерживать существующих и привлекать новых потребителей, аккумулировать опыт и знания персонала;

3) при использовании системы показателей соблюдается баланс между стратегическим и оперативным уровнями управления, прошлыми и будущими результатами, внутренними и внешними аспектами деятельности предприятия.

Рассматривая сбалансированную систему показателей как одну из технологий реализации стратегии управления, отметим, что она не является единственно верной и гарантированно результативной, но в современных условиях хозяйствования применяется в достаточной мере широко и стала одним из стандартных решений для организаций, ориентированных на стратегию развития.

ССП включает в себя несколько ключевых компонент:

• структурирование деятельности организации как единой системы из четырех взаимосвязанных составляющих (финансовой, клиентской, внутренних процессов, обучения и роста);
• построение стратегической карты, отражающей стратегические цели в разрезе этих перспектив и взаимосвязь между ними;
• формирование управленческих показателей, отражающих цели деятельности организации [4].

Отражая целостный подход к управлению сложной системой, ССП позволяет выстроить четкую взаимосвязь стратегических целей и показателей, выявить факторы и условия достижения итоговых результатов [11]. Важнейшим свойством ССП является не просто наличие целей и показателей по разным аспектам деятельности, но и причинно-следственные связи между ними, которые показывают, в какой последовательности следует осуществлять управленческие действия (а также то, чем заниматься не следует, поскольку это не вносит вклада в достижение стратегических целей). В конечном итоге это дает возможность ранжировать управленческие действия, определять их приоритет и первостепенную важность.

Вышесказанное, на наш взгляд, может являться обоснованием применения, на основе ССП, системного подхода, включающего математическое моделирование и разработку алгоритмов теоретического и численного анализа деятельности производственного предприятия.

В связи с этим, для обоснования и объективной оценки применения ССП, требуется разработка математических моделей управления деятельностью производственных предприятий, включая предприятия сельскохозяйственной отрасли [1, 2, 5–10].

При разработке моделей крупных социально-экономических систем и оценке эффективности их функционирования, в связи с наличием множества определяющих факторов, возникают проблемы взаимной увязки операционных, инвестиционных, финансовых потоков, что, в частности, порождает необходимость автоматизированной обработки большого количества данных, используемых в процессе моделирования. В этом случае необходимо использовать автоматизированные средства анализа, эффективность применения которых зависит от сбалансированности математических моделей, лежащих в основе алгоритмов их работы.

Рассмотрим следующую модель деятельности такого предприятия сельскохозяйственной отрасли, как свинокомплекс, который производит два вида продукции – мясо в живом весе (продукт 1) и мясо в убойном весе (продукт 2).

Введем следующие обозначения.

m1 – количество работников, занятых на производстве продукции 1-го вида;

m2 – количество работников, занятых на производстве продукции 2-го вида;

n1 – выпуск продукции 1-го вида;

n2 – выпуск продукции 2-го вида;

S – размер кредита для финансирования деятельности предприятия;

Dot – размер государственных дотаций для функционирования предприятия.

Примем, что для производства продукции 1-го вида используется один комплект основных производственных фондов (ОПФ) – свиноферма (СФ), а для производства продукции 2-го вида используется комплект ОПФ убойного пункта (УП). При этом выполняется естественное условие n1 ≥ n2, означающее, что выпуск мяса в убойном весе не превосходит выпуск мяса в живом весе. Необходимо определить, сколько работников свинофермы и УП использовать для производства продукции свинокомплекса, чтобы максимизировать его чистую приведенную стоимость (NPV).

В этой связи введем следующие обозначения:

Т – горизонт планирования, годы/месяцы;

r – ставка дисконтирования (доля);

с1 – стоимость СФ (ден.ед/ед.ОПФ);

с2 – стоимость УП (ден.ед/ед.ОПФ);

P1 – стоимость единицы продукции 1, (ден. ед./ед. продукции);

P2 – стоимость единицы продукции 2, (ден. ед./ед. продукции);

V1 – производительность работника СФ за период Т, ед. продукции/работник;

V2 – производительность работника УП за период Т, ед. продукции/работник;

T1 – время полезного использования СФ, ед. вр.;

T2 – время полезного использования УП, ед. вр.;

q1 – спрос на продукцию 1 за период Т, ден. ед.;

q2 – спрос на продукцию 2 за период Т, ден. ед.;

θ1 – стоимость всех видов сырья, затраченного на производство единицы продукции 1, ден. ед.;

θ2 – стоимость всех видов сырья, затраченного на производство единицы продукции 2, ден. ед.;

S1 – заработная плата одного работника СФ за период Т, ден. ед.,

S2 – заработная плата одного работника УП за период Т, ден. ед.,

αi (i = 1, 2, 3, 4) – ставки налогов на добавленную стоимость, на имущество, на прибыль и страховые взносы в социальные фонды соответственно;

β1 – доля выручки от продажи продукции свинокомплекса, затрачиваемая на рекламу,

β2 – доля выручки от продажи продукции свинокомплекса, затрачиваемая на обучение (переобучение) персонала;

Т0 – срок кредита;

r0 – годовая ставка кредита;

Smax – максимальная сумма кредита, ден. ед.;

Dotmax – максимальная сумма дотации, ден. ед.;

DS0 – первоначальная сумма собственных средств производителя.

Авторами разработана следующая математическая модель деятельности сельскохозяйственного предприятия, функционирующего в рамках сбалансированной системы показателей, которая описывается в форме задачи линейного программирования (ЗЛП):

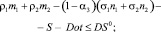(1)

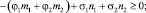(2)

n1 ≤ V1m1; (3)

n2 ≤ V2m2; (4)

P1n1 ≤ q1; (5)

P2n2 ≤ q2; (6)

S ≤ Smax; (7)

Dot ≤ Dotmax; (8)

n2 ≤ n1; (9)

m1 ≥ 0, m2 ≥ 0, n1 ≥ 0, n2 ≥ 0;

S ≥ 0, Dot ≥ 0; (10)

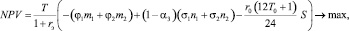(11)

где ρ1 = c1(1 – T/T1) + (1 – α3)φ1;

ρ2 = c2(1 – T/T2) + (1 – α3)φ2;

φ1 = c1(α2 + (1 – α2)T/T1) + (1 + α4)S1;

φ2 = c2(α2 + (1 – α2)T/T2) + (1 + α4)S2;

σ1 = (1 – α1 – β1 – β2)P1 – θ1;

σ2 = (1 – α1 – β1 – β2)P2 – θ2;

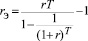– эффективная ставка дисконтирования, учитывающая динамические особенности показателя NPV.

Модель (1)–(11) можно рассматривать, как модель любого производственного предприятия, использующего в качестве основного ресурса рабочую силу. В данной модели учитываются как особенности бизнес-планирования, так и бухгалтерские особенности функционирования предприятия. В частности, в качестве производственных затрат рассматриваются такие статьи, как амортизация, фонд оплаты труда, материальные затраты, в качестве финансовых рассматриваются налоговые затраты, а также использование заемных средств, дотации предприятию. С точки зрения оценки эффективности инвестиционных проектов модель учитывает такие стратегические составляющие доходов и затрат, как прибыль, оценку имущества и инвестиции предприятия.

Сделаем ряд замечаний по модели (1)–(11). Содержательно неравенство (1) отражает условие платежеспособности предприятия на всем горизонте планирования, неравенство (2) – неотрицательность прибыли, неравенства (3), (4) – условия ограниченности эффективности ОПФ, (5), (6) – рыночные ограничения спросом на объемы производства продукции, (7), (8) – финансовые ограничения максимальными объемами кредита и дотаций, (9) – естественное производственное условие, означающее, что выпуск мяса в убойном весе (продукт 2) не может превышать выпуск мяса в живом весе (продукт 1); (10) – естественные ограничения неотрицательности значений искомых переменных. Отметим, что модель (1)–(11) косвенно учитывает присутствие в экономической системе финансового игрока (через параметр максимального объема кредита Smax), а также управленца (через параметр максимального объема дотаций Dotmax). Критерий (11) представляет собой условие максимизации статического аналога чистой приведенной стоимости инвестиционно-производственного проекта. Отметим, что, поскольку выражение T/(1 + rэ) в соотношении (11) положительно, то оно не меняет решения оптимизационной задачи (1)–(11) в пространстве переменных, и его можно исключить, если требуется определить лишь оптимальные значения количества работников, объемов производства продукции и размеров заемного финансового ресурса. Очевидно, набор нулевых значений переменных задачи (1)–(11) является допустимым, поэтому множество допустимых значений переменных указанной задачи непусто. При этом данному набору значений переменных соответствует естественное, с экономической точки зрения, нулевое значение целевого критерия NPV = 0, поэтому для оптимального значения целевого критерия NPV* справедливо следующее неравенство NPV *≥ 0, причем однозначным условием неэффективности анализируемого проекта будет условие NPV = 0.

Учитывая, что модель (1)–(11) описывается задачей линейного программирования, а также непустоту множества допустимых значений ее переменных, нетрудно доказать существование решения задачи, описываемой моделью (1)–(11). Для этого достаточно показать ограниченность переменных указанной задачи, используя задействованные в ее ограничениях условия. Существование указанного решения служит теоретическим обоснованием допустимости применения к анализу задачи, при различных содержательно приемлемых значениях ее исходных параметров, методов численного анализа (например, симплекс-метода и его модификаций, реализованных в пакете прикладных программ, работа которого подробно описана в [3]. Предварительные расчеты на модельных данных, проведенные с использованием описанного пакета, показали существование решения исследуемой задачи в широком диапазоне ее параметров.

Заключение

Следует отметить, что в предложенной модели соблюден баланс между стратегическим и оперативным уровнями управления, учтены элементы всех составляющих, используемых в ССП:

1) внутренние процессы (определяются оптимальные количества работников и производства продукции) описаны с помощью общепринятых методов оценки эффективности производственных проектов;

2) процессы финансирования – через переменные, определяющие оптимальные объемы заемных ресурсов, дотаций, причем условие неотрицательности собственных средств гарантирует платежеспособность предприятия на всем горизонте планирования;

3) CRM-процессы (клиенты) – через ограничения объемов производства уровнем потребительского спроса;

4) процессы обучения и роста – через параметры затрат на обучение персонала и продвижение продукции (рекламных затрат).

Таким образом, модель (1)–(11) логически связывает ключевые составляющие ССП, учитывает взаимодействие потоков материального (количество работников и объем производства) и нематериального (финансовая, рекламная деятельность, деятельность по обучению персонала) характера, что позволяет аккумулировать опыт и знания персонала.

Учитывая, что модель (1)–(11) является оптимизационной, можно рассчитывать на получение количественных параметров оптимального распределения указанных составляющих ССП, автоматически выявляющих социально-экономический потенциал функционирования предприятий, групп предприятий, отраслей, направлений экономической деятельности на местном, региональном и национальном уровнях.

Библиографическая ссылка