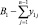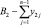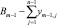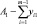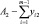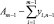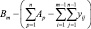В период кризисных явлений в экономике одной из наиболее актуальных задач, встающих перед работодателями, является оптимизация количественной и качественной структуры персонала компании в зависимости от изменяющейся рыночной конъюнктуры.
В научной литературе и периодических публикациях большое внимание уделено проблематике оптимизации персонала на предприятиях различных видов деятельности. Этой тематике посвящены работы В.П. Пугачева, А.Я. Кибанова, С.П. Дынина, С.В. Шекшня и других авторов. Механизмы решения задач оптимизации кадрового состава также определены законодательством РФ (Трудовой кодекс ст. 81 (п. 2, 3), 128, 93, 73, 157) [4]. Среди подходов, позволяющих оптимизировать численный и профессиональный состав компании, авторами предлагаются такие, как: формирование возрастного соотношения работников в структуре предприятия, сокращение штатов, развитие профессиональных компетенций сотрудников, аутсорсинг бизнес-процессов, аутстаффинг, кадровое планирование [2, 3, 4].
Одним из методов, позволяющих решить задачу оптимизации персонала и одновременно повысить эффективность бизнес-процессов, является использование аутсорсинга [2]. Следовательно, аутсорсинговые компании можно рассматривать как один из инструментов, позволяющих обеспечить регулирование рынка труда, что показано в [1].
Однако проблема оптимизации персонала в самих аутсорсинговых компаниях также стоит достаточно остро. Это обусловлено двумя особенностями их функционирования:
1. Дифференциацией компетенций сотрудников, ориентированных на решение различного рода задач, как широкого, так и узкого профиля.
2. Необходимостью равномерной загруженности поступающих потоков заявок на обслуживание клиентов.
Одной из основных задач аутсорсинговых компаний является соответствие количественных, качественных, временных и стоимостных характеристик оказываемых услуг критериям, закрепленным в договоре на обслуживание.
Кадровый состав аутсорсинговой компании, как правило, имеет в своей структуре как специалистов широкого профиля, способных решать наиболее востребованные на рынке задачи, так и сотрудников, состав компетенций которых позволяет выполнять узконаправленные работы по специфическим профессиональным направлениям.
В подобных случаях перед руководством предприятия встает вопрос об оптимизации кадрового состава в зависимости от двух основных критериев, определяющих эффективное выполнение задач компании в соответствии с договорами аутсорсингового обслуживания.
К таким критериям можно отнести:
1) соответствие степени загруженности работников оптимальному значению текущих объемов работ;
2) развитие спектра компетенций у имеющихся сотрудников либо расширение штата за счет трудоустройства новых специалистов, имеющих узконаправленные, но востребованные на рынке профессиональные знания и опыт.
На сегодняшний день практика разрешения данной проблематики заключается в приблизительном, базирующемся на эмпирическом опыте руководства подходе при распределении нагрузки между сотрудниками и соответствующей оптимизации кадрового состава.
Описание метода
В данной статье предлагается математически обоснованный механизм перераспределения нагрузки между специалистами компании в зависимости от набора их компетенций и объема поступающего потока разнотипных задач.
При рассмотрении предлагаемого метода решения поставленной выше задачи примем следующие допущения:
1. Объем заявок, поступающих на обслуживание, достаточен для их обработки в аутсорсинговой системе.
2. Спектр компетенций, которыми обладают специалисты аутсорсинговой компании, достаточен для выполнения задач, поставленных контрагентами.
Пусть для определённой фирмы имеется набор из n видов работ или услуг, имеющих объёмы А1, А2,…, Аn (в расчёте на рабочую неделю или рабочий месяц), для реализации которых имеется m сотрудников, для каждого из которых нормировано их общее рабочее время B1, B2,…, Bn (также в расчёте на рабочую неделю или рабочий месяц). Схема этого процесса показана на рисунке. Кроме того, известно, что каждый из сотрудников обладает определённым набором компетенций, то есть набором видов работ, которые он способен выполнять.
Требуется составить алгоритм для оптимизации распределения видов работ по каждому из сотрудников для следующих случаев:
1) номинальной загрузки (штатного режима сотрудников, а также штатного потока по всем видам работ);
2) загрузки в случае выбывания из производственного процесса какого-либо (или каких-либо) из сотрудников;
3) загрузки для случая неравноценности видов работ (например, по их стоимости).
Введём понятие матрицы компетенций. Определим, что матрица компетенций есть математическое представление спектра компетенций сотрудников компании, где соответственно отображены возможности элементов матрицы (сотрудников), имеющих либо не имеющих достаточного квалификационного уровня для выполнения тех или иных видов работ.
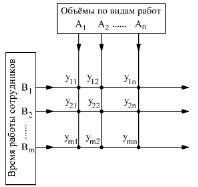
Схема обработки заказов, поступающих на обслуживание в аутсорсинговую систему
Представим матрицу компетенций в виде K – матрицы, каждый элемент которой kij равен 0 в случае неспособности i-го сотрудника выполнять j-й вид работ, и 1 в случае его способности выполнять данный вид работ. Тогда элемент матрицы yij будет иметь смысл времени, затраченного i-м сотрудником для выполнения j-го вида работы, если
yij = kij·xij, (1)
где xij – элемент матрицы, соответствующий теоретической возможности i-го сотрудника выполнять j-й вид работ. Таким образом, введение матрицы K позволяет, с одной стороны, устранить из рассмотрения все нулевые (для данного набора сотрудников) элементы матрицы X, а с другой – разработать более общий алгоритм, учитывающий возможности изменения набора компетенций (при приёме нового сотрудника или повышения квалификации старого) для каждого из сотрудников.
Исключив зависимые переменные, можно составить соответствующие линейные задачи оптимизации, решив их любыми известными в математике способами [5–7].
Допустим, что матричные элементы yij – найденные объёмы работ i-го типа работы для j-го сотрудника. Тогда, согласно рисунку, получим следующую таблицу для искомых переменных:
Таким образом, получим следующую систему m + n – 1 линейных неравенств:
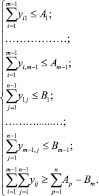 (2)
(2)
Система неравенств (2) определяет допустимое множество значений D, в области которого возможна нормальная работа сотрудников.
Кроме того, при решении задачи 3 к этой системе неравенств следует добавить целевую функцию, определяемую неравноценностью видов работ по отношению к их стоимостям:
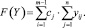 (3)
(3)
Здесь cj есть известные элементы вектора стоимостей для каждого вида работ. Разумеется, в целевой функции (3), как и в системе (2), присутствуют лишь те из элементов yij, которым соответствует ненулевые элементы матрицы K (условие (1)).
Таблица 1
Исключение зависимых переменных
|
y11 |
y12 |
… |
y1,n–1 |
|
|
y21 |
y22 |
… |
y2,n–1 |
|
|
… |
… |
… |
… |
… |
|
ym–1,1 |
ym–1,2 |
… |
ym–1,n–1 |
|
|
|
|
… |
|
|
Рассмотренная задача может быть сведена к транспортной, поскольку полностью соответствует ей по форме общего вида [5–7]. Значит, она может быть решена каким-либо из стандартных способов, например, методом северо-западного угла или симплекс-методом.
Для примера решим задачи 1, 2, 3 для следующей матрицы компетенций:
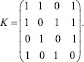 (4)
(4)
Пусть величины объёмов работ в расчёте на 40-часовую рабочую неделю равны:
A1 = 35; A2 = 55; A3 = 25; A4 = 45 (в сумме 160 часов).
Оптимизируем объёмы работ таким образом, чтобы на каждого из сотрудников приходилось по 40 часов рабочего времени. Данное решение соответствует закрытой транспортной задаче.
Запишем пробное решение в виде табл. 2.
Таблица 2
Пробное решение к задаче 1
|
A1 |
A2 |
A3 |
A4 |
||
|
B1 |
35 |
5 |
40 |
||
|
B2 |
40 |
40 |
|||
|
B3 |
10 |
25 |
5 |
40 |
|
|
B4 |
40 |
40 |
|||
|
35 |
55 |
25 |
45 |
160 |
Таблица 3
Одно из возможных решений задачи 1
|
A1 |
A2 |
A3 |
A4 |
||
|
B1 |
20 |
20 |
40 |
||
|
B2 |
20 |
20 |
40 |
||
|
B3 |
35 |
5 |
40 |
||
|
B4 |
35 |
5 |
40 |
||
|
35 |
55 |
25 |
45 |
160 |
Таблица 4
Пробное решение задачи 2
|
A1 |
A2 |
A3 |
A4 |
||
|
B2 |
35 |
18 |
53 |
||
|
B3 |
37 |
16 |
53 |
||
|
B4 |
9 |
44 |
53 |
||
|
35 |
55 |
25 |
45 |
160 |
Таблица 5
Одно из возможных решений к задаче 2
|
A1 |
A2 |
A3 |
A4 |
||
|
B2 |
7 |
2 |
44 |
53 |
|
|
B3 |
53 |
53 |
|||
|
B4 |
28 |
25 |
53 |
||
|
35 |
55 |
25 |
45 |
160 |
Согласно методу северо-западного угла [5–7], будем «перемещать» данные до тех пор, пока все «светлые» ячейки не окажутся пустыми. При этом мы получим одно из возможных решений для загрузки сотрудников.
Рассмотрим задачу 2: пусть 1-й сотрудник временно отсутствует. Запишем транспортную задачу и решим её, поделив высвободившуюся нагрузку между остальными сотрудниками (получим 53 часа):
Далее, аналогичным способом получим решение.
Видно, что нераспределёнными остались 2 часа рабочего времени, которые можно не учитывать, как малую величину.
Рассмотрим задачу 3: пусть известны стоимости для всех видов работ в расчёте на 1 час и требуется распределить нагрузку между сотрудниками таким образом, чтобы прибыль от их работы была максимальной.
При такой постановке вопроса логично будет решать открытую транспортную задачу [5–7], поскольку подобная оптимизация может иметь место лишь при объёме работ, превышающем номинальный для данного состава сотрудников, то есть при условии
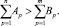 (5)
(5)
Составим таблицу для решения открытой транспортной задачи, исходя из следующих данных:
A1 = 60; A2 = 70; A3 = 50;
A4 = 60 (в сумме 240 часов);
удельные стоимости по всем видам работ заданы вектором С:
c1 = 400; c2 = 200;
c3 = 100; c4 = 300 (руб./ч).
Как известно, открытая транспортная задача может быть сведена к закрытой введением фиктивного сотрудника (B5), стоимость работ для которого равна нулю. Для выполнения расчетов, заполним соответствующую таблицу с пробным решением.
Прибыль от пробного решения равна
P = 16 + 8 + 2 + 8 + 2 = 36 тыс. руб.
Будем перемещать ячейки таким образом, чтобы прибыль возрастала. Проверим полученное решение методом потенциалов.
Он показывает, что улучшить решение невозможно.
Окончательная прибыль:
P = 16 + 8 + 6 + 12 + 4 = 46 тыс. руб.
Таблица 6
Пробное решение к задаче 3
|
A1 |
A2 |
A3 |
A4 |
||
|
B1 |
400 |
200 |
300 |
40 |
|
|
40 |
|||||
|
B2 |
400 |
100 |
300 |
40 |
|
|
20 |
20 |
||||
|
B3 |
200 |
300 |
40 |
||
|
40 |
|||||
|
B4 |
400 |
100 |
40 |
||
|
30 |
10 |
||||
|
B5 |
80 |
||||
|
30 |
50 |
||||
|
60 |
70 |
50 |
60 |
240 |
Таблица 7
Одно из оптимальных решений задачи 3
|
(0) A1 |
(0) A2 |
(100) A3 |
(–100) A4 |
||
|
(400) B1 |
400 |
200 |
300 |
40 |
|
|
40 |
|||||
|
(400) B2 |
400 |
100 |
300 |
40 |
|
|
20 |
20 |
||||
|
(400) B3 |
200 |
300 |
40 |
||
|
40 |
|||||
|
(0) B4 |
400 |
100 |
40 |
||
|
0,01 |
39,99 |
||||
|
B5 |
80 |
||||
|
70 |
10 |
||||
|
60 |
70 |
50 |
60 |
240 |
Для упрощения реализации предложенного метода целесообразно использование программного обеспечения MathCad, что позволит производить вышеприведенные расчеты в автоматическом режиме и удобной форме для руководителей компаний.
Таким образом, все три задачи могут быть решены предложенным способом.
В заключение необходимо отметить, что предложенный метод позволяет решать задачи распределения нагрузки между специалистами, а также проблему оптимизации персонала и в других сферах хозяйственной деятельности. Например, в медицинских и образовательных учреждениях, авторизованных сервисных центрах по обслуживанию различных видов технических устройств и так далее. Таким образом, рассмотренные пути решения данной проблематики могут быть реализованы в широком спектре областей народного хозяйства.
Библиографическая ссылка
Балдин О.В., Воржев В.Б., Иванов Г.И. РАЗРАБОТКА МЕТОДИКИ РАСПРЕДЕЛЕНИЯ НАГРУЗКИ МЕЖДУ СПЕЦИАЛИСТАМИ АУТСОРСИНГОВОЙ КОМПАНИИ // Фундаментальные исследования. 2016. № 4-2. С. 355-360;URL: https://fundamental-research.ru/ru/article/view?id=40181 (дата обращения: 21.02.2026).