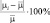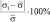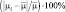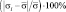В связи с увеличением новых классов телекоммуникационных устройств и соответствующих сервисов увеличиваются не только объемы передаваемых информационных потоков (например, по данным Cisco Visual Networking Index (наглядные показатели Сети) объемы передаваемого интернет-трафика увеличились со 100 Гб за одни сутки в 1992 г. до 16 000 Гб за 1 секунду в 2014 г. [23]), но изменяется и собственно структура трафика (в настоящее время не более 60 % от общего объема трафика генерируется персональными компьютерами, в то время как его остальной объем обеспечивают смартфоны, планшеты, телевизоры, бытовая техника (интернет-вещи) и др.).
В этой связи закономерно возрастают требования к гибкости и масштабируемости компьютерных сетей, которым зачастую уже не соответствуют классические (по сути, статические) коммуникационные сети, становящиеся ограничивающим фактором развития телекоммуникаций. Например, традиционные архитектуры/дизайны сетей становятся неэффективными в динамических средах. При этом классические подходы, основанные на распределенном управлении устройствами традиционных сетей (например, виртуальные сети (VLAN)), не соответствуют современному уровню развития виртуализации серверов и систем хранения данных, а также требованиям крупного бизнеса и сервис-провайдеров (AT&T, Verizon, Google, Facebook, Microsoft и др.).
Для эффективного решения вышеперечисленных проблем и проектирования сетей нового поколения, в том числе и виртуальных программно-конфигурируемых сетей - SDN (Software-defined Networking), необходимо понимать, какие типы сессий информационного обмена (двунаправленное соединение отправитель - получатель) проходят через каналы передачи данных, каковы их размеры, длительность и частоты возникновения, как они взаимодействуют между собой, какое влияние и в какие моменты оказывают на загрузку канала.
Продолжительное время считалось, что трафик в компьютерных сетях описывается классическим Пуассоновским распределением. Однако в 1993 г. W. Leland, M. Taqqu, W. Willinger и D. Wilson привели в своей работе результаты, с их точки зрения, свидетельствующие о самоподобной природе интернет-трафика [24]. С этого момента большинство работ, посвященных исследованиям сетевого трафика [17, 20, 8, 18], ссылаясь на работы, следующие [24], исходят из априорного предположения о самоподобной природе телетрафика. При этом большинство авторов использует устаревшие дампы трафика, полученные в 90-х гг. ХХ в. [9], и модели трафика, утратившие свою актуальность [7, 1]. Также необходимо отметить, что многие авторы изучают искусственный трафик, передаваемый в тех или иных модельных локальных вычислительных сетях (ЛВС) [21, 4, 19], или трафик, синтезированный с помощью программных реализаций известных математических моделей (SPSS [25], on-off-модель [6], жидкостная модель [2] и гибридная жидкостная модель [3]) программных генераторов трафика (NS-2, NS-3 [30]), свойства которых, очевидно, существенно отличаются от свойств реальных информационных процессов, протекающих в корпоративных ЛВС или провайдерских магистралях.
Таким образом, задача исследования количественных характеристик современного трафика с использованием более сложных представлений о структуре информационных потоков и принципах их формирования является актуальной задачей. В статье изложены результаты анализа статистических свойств интернет-трафика, в котором, в отличие от ранее выполненных другими авторами работ, трафик в магистральном канале рассматривается как совокупность сессий, относящихся, в зависимости от объемов переданной информации за время существования данной сессии, к одному из трех классов: «Мыши» (менее 0,3 Мбайт), «Мулы» (от 0,3 до 10 Мбайт) или «Слоны» (более 10 Мбайт).
1. Объект исследования
В качестве объекта исследования выбраны ежедневные (за период одной недели) пятнадцатиминутные дампы трафика магистрального канала между США и Японией, находящиеся в хранилище данных MAWI (Measurement and Analysis on the WIDE Internet) [26]. Здесь находится как актуальная информация о текущем состоянии интернет-канала, так и архивные данные, начиная с 1999 г. Средний размер одного дампа составляет около 10 Гб. Для сохранения конфиденциальности информации в дампе обезличены сведения о конкретных пользователях, а содержание пакетов (полезная нагрузка) заменено на сгенерированные случайным образом данные с сохранением при этом оригинального размера пакетов. Это позволяет сохранить всю необходимую для исследований техническую информацию (номера портов, протоколы, размер пакета и т.д.), содержащуюся в дампе.
2. Выбор групп сессий, создающих информационные потоки
Следуя [27], для классификации сессий информационного обмена была использована трехкомпонентная модель.
Класс А – «Слоны»: объем данных, передаваемых сессией, больше либо равен 10 Мбайт (P2P, торренты, скачивание больших файлов), время жизни таких сессий велико.
Класс B – «Мулы»: объем данных, передаваемых сессией, составляет от 0,3 до 10 Мбайт (просмотр видеороликов, прослушивание музыки, скачивание файлов небольших размеров).
Класс С – «Мыши»: объем данных, передаваемых сессией, составляет менее 0,3 Мбайта (ICQ-сообщения, просмотр WEB-страниц и т.д.).
Здесь сессия – двунаправленный информационный обмен между приложением отправителя, инициировавшим соединение, и приложением получателя; поток – пакеты всех сессий одного класса, проходящих через канал, на временном интервале, равном окну агрегации. Принадлежность сессии информационного обмена к соответствующему классу определялась на основе анализа объемов данных, переданных за время ее существования.
3. Технология классификации потоков [10]
Анализ дампа проводился в два этапа. На первом этапе осуществлялся семантический анализ файлов, содержащих дамп трафика, позволяющий выбрать количественные показатели трафика, удовлетворяющие заданным условиям, и передать их автоматически в рабочее пространство пакета MATLAB. Для переноса параметров пакетов дампа (необходимых в том числе для определения сессий информационного обмена выбранных классов) в окружение MATLAB использовался специализированный программный инструмент [16], подробно описанный в [11]. В связи с тем, что максимальный (для используемой в исследованиях ЭВМ) объем данных, который можно разместить в рабочем пространстве MATLAB, не нарушив при этом стабильность его работы, составляет 400 Мбайт – информация о временном интервале длительностью около 1 мин, исходный файл дампа трафика делился на части соответствующей длительности, которые обрабатывались по отдельности.
После того как данные о пакетах из дампа оказывались перенесенными в MATLAB, определялось, к сессии какого класса принадлежит каждый пакет. Используя информацию о принадлежности пакета к сессии конкретного класса, для заданных окон агрегации формировались три класса потоков. При этом принималось, что:
– сессия состоит из пакетов, передаваемых приложениями отправителя и получателя, в прямом и обратном направлениях;
– объем трафика равняется суммарному объему пакетов, переданных в течение сессии.
Для отнесения конкретного пакета к соответствующей сессии и вычислению объема передаваемой в ней информации использовалась следующие данные, извлекаемые из дампа:
– время прохождения пакета через узел записи дампа;
– размер пакета (включая передаваемые данные);
– IP-адрес отправителя пакета;
– IP-адрес получателя пакета;
– порт отправителя пакета;
– порт получателя пакета;
– тип протокола.
4. Аппаратные средства технологии работы с дампом
Средний размер исследуемых дампов составляет около 10 Гб, а приблизительное время обработки на одном ядре процессора составляет около 960 часов. Для сокращения времени обработки дампа в технологию его обработки была добавлена возможность проведения параллельных вычислений, что позволило использовать многоядерные процессоры и кластеры, в том числе суперкомпьютер УРАН Института математики и механики УрО РАН и, соответственно, сократить время обработки дампа в 100 раз (до 7–8 часов для одного дампа) при использовании 120 ядер центрального процессора.
При обработке были задействованы 15 вычислительных модулей со следующими параметрами:
– два 4-ядерных процессора Intel® Xeon® E5450 (3,0 GHz);
– оперативная память 16 GB PC2-5300, Registered DDR2-667;
– кэш-память 2×6 MB Level 2 cache (5400 Sequence).
Статистические свойства трафика в магистральном интернет-канале
В результате обработки были получены случайные последовательности (СП), содержащие «мгновенные» значения числа пакетов Ni и объемов данных Vi, переданных в течение 15 минут в каждый из дней одной недели. К СП Ni и Vi в ходе проведенных исследований применялась процедура агрегирования, состоящая в разбиении трафика на временные интервалы длительностью t = 0,1; 1,0 с (окна агрегации) и подсчете на данном окне агрегации интегральных значений соответствующих характеристик трафика. Для краткости в обозначение каждой из СП добавлено значение окна агрегации: 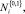
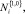
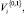
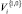 соответственно.
соответственно.
1. Статистические свойства временных рядов Ni, Vi
Анализ статистических свойств СП Ni, Vi, проведенный в [29, 22], показал, что изученные случайные последовательности относятся к классу СП с ограниченной областью рассеяния. При этом для аппроксимации плотности распределения (ПР) СП 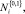
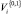 следует использовать аппроксимацию Розенблатта - арзена [12, 28], для СП
следует использовать аппроксимацию Розенблатта - арзена [12, 28], для СП 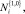
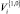 – метод мнимых источников, в соответствии с которым ПР ищется в виде линейной комбинации функций распределений с центрами, совпадающими с положением мнимых источников (рис. 1):
– метод мнимых источников, в соответствии с которым ПР ищется в виде линейной комбинации функций распределений с центрами, совпадающими с положением мнимых источников (рис. 1):
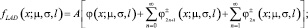 (1)
(1)
где А – нормировочный коэффициент, определяемый из условия:
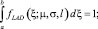 (2)
(2)
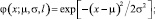
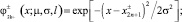
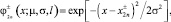
где 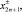
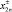 вычисляются по формулам
вычисляются по формулам
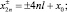
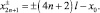 (3)
(3)

Рис. 1. Линейная комбинация функций распределений
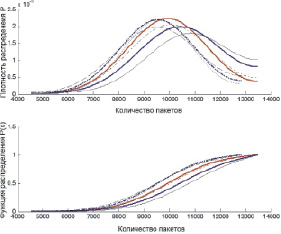
а
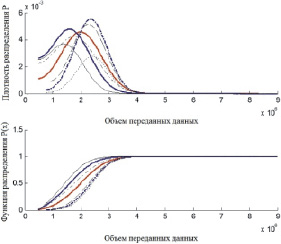
б
Рис. 2. Типичные плотности распределения (вверху) и функции распределения (внизу): а – числа пакетов, передаваемых классом «Мыши» за 0,1 с, б – объема данных, передаваемого классом «Слоны» за 0,1 с, аппроксимированные в соответствии с (1) и (2)
Здесь для нахождения оценок параметров ПР СП 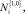
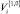 использовалась методика, основанная на применении генетических алгоритмов, описанная в [13, 14].
использовалась методика, основанная на применении генетических алгоритмов, описанная в [13, 14].
На рис. 2, а представлены примеры плотностей распределения и функции распределения числа пакетов, переданных «Мышами» за 0,1 с, а на рис. 2, б – типичные плотности распределения и функции распределения объема данных, передаваемых классом «Слоны» за 0,1 с. Здесь и далее число мнимых источников в (1), (2) равно 5.
Результаты вычисления параметров ФР СП, содержащих агрегированные значения Ni, Vi, переданных в течение временного интервала, равного длительности окна агрегации, представлены в табл. 1 и 2. (Здесь 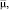
 - средние по семи дням значения параметров распределения).
- средние по семи дням значения параметров распределения).
Данные, представленные в табл. 1−2, позволили оценить вариативность параметров ФР μ, σ относительно средних значений 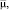
 изученных СП (табл. 3), а также вычислить значения коэффициентов пропорциональности между
изученных СП (табл. 3), а также вычислить значения коэффициентов пропорциональности между 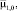
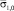 и
и 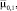
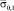 , соответственно αμ, ασ (табл. 4).
, соответственно αμ, ασ (табл. 4).
Таблица 1
Параметры ФР СП Ni, вычисленные по дампу трафика в каждый из семи дней
|
Класс |
τ |
|
|
|
|
||||||||||||
|
i = 1 |
i = 2 |
i = 3 |
i = 4 |
i = 5 |
i = 6 |
i = 7 |
i = 1 |
i = 2 |
i = 3 |
i = 4 |
i = 5 |
i = 6 |
i = 7 |
||||
|
«Мыши» |
0,1 |
9813 |
1,60 |
5,92 |
2,59 |
1,30 |
0,09 |
1,07 |
9,19 |
1772 |
26,72 |
27,91 |
2,02 |
9,71 |
4,66 |
36,05 |
25,64 |
|
1 |
97901 |
1,33 |
6,04 |
2,36 |
1,54 |
0,25 |
0,61 |
8,98 |
8992 |
18,03 |
26,44 |
12,28 |
7,04 |
0,75 |
17,34 |
33,12 |
|
|
«Мулы» |
0,1 |
666 |
54,05 |
68,70 |
45,11 |
8,58 |
53,94 |
66,41 |
56,09 |
434 |
21,31 |
8,17 |
16,74 |
2,32 |
24,67 |
4,61 |
14,13 |
|
1 |
7409 |
42,41 |
51,60 |
30,23 |
1,96 |
27,68 |
47,77 |
50,75 |
2915 |
21,53 |
1,14 |
2,13 |
0,82 |
4,50 |
17,14 |
7,07 |
|
|
«Слоны» |
0,1 |
3004 |
34,42 |
4,62 |
6,22 |
24,45 |
16,55 |
38,10 |
35,74 |
722 |
10,50 |
0,25 |
17,63 |
48,54 |
14,48 |
20,30 |
35,84 |
|
1 |
30029 |
34,51 |
4,66 |
6,20 |
24,40 |
16,53 |
38,15 |
35,74 |
5663 |
1,45 |
0,88 |
18,46 |
54,38 |
13,35 |
13,09 |
33,85 |
|
Таблица 2
Параметры ФР СП Vi, вычисленные по дампу трафика в каждый из семи дней
|
Класс |
τ |
|
|
|
|
||||||||||||
|
i = 1 |
i = 2 |
i = 3 |
i = 4 |
i = 5 |
i = 6 |
i = 7 |
i = 1 |
i = 2 |
i = 3 |
i = 4 |
i = 5 |
i = 6 |
i = 7 |
||||
|
«Мыши» |
0,1 |
555543,79 |
3,30 |
1,05 |
10,83 |
9,89 |
19,85 |
3,52 |
32,70 |
2444194,95 |
2,40 |
17,25 |
4,57 |
4,96 |
11,17 |
8,02 |
9,99 |
|
1 |
4084729,38 |
3,76 |
6,02 |
21,23 |
17,96 |
33,50 |
15,17 |
59,77 |
24441716,74 |
2,49 |
17,23 |
4,46 |
4,99 |
11,31 |
8,30 |
9,55 |
|
|
«Мулы» |
0,1 |
467893,92 |
8,26 |
2,63 |
7,50 |
3,56 |
28,93 |
14,24 |
14,53 |
706542,71 |
51,48 |
77,74 |
21,53 |
19,94 |
65,29 |
48,16 |
57,25 |
|
1 |
3394353,41 |
2,25 |
1,35 |
7,68 |
9,54 |
16,44 |
8,09 |
6,41 |
7434381,93 |
45,97 |
68,95 |
17,26 |
15,37 |
35,08 |
57,25 |
55,21 |
|
|
«Слоны» |
0,1 |
933262,70 |
11,61 |
4,31 |
15,78 |
58,04 |
13,45 |
20,67 |
42,36 |
3449532,25 |
43,09 |
8,01 |
10,35 |
23,87 |
13,80 |
42,10 |
36,32 |
|
1 |
7414378,04 |
1,16 |
5,67 |
14,87 |
68,46 |
9,83 |
13,33 |
43,26 |
34470949,62 |
43,41 |
8,07 |
10,15 |
23,11 |
13,95 |
42,03 |
36,36 |
|
Таблица 3
Максимальные значения вариаций параметров ПФР СП Ni, Vi
|
СП |
Класс |
Δμ0,1, % |
Δσ0,1, % |
Δμ0,1, % |
Δσ0,1, % |
|
Ni |
«Мыши» |
9,19 |
30,05 |
8,98 |
31,20 |
|
«Мулы» |
68,70 |
24,67 |
51,60 |
21,53 |
|
|
«Слоны» |
38,10 |
48,54 |
38,15 |
54,38 |
|
|
Vi |
«Мыши» |
17,25 |
32,70 |
17,23 |
59,77 |
|
«Мулы» |
77,74 |
28,93 |
68,95 |
16,44 |
|
|
«Слоны» |
43,09 |
58,04 |
43,41 |
68,46 |
Таблица 4
Коэффициенты пропорциональности между 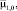
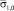 и
и 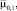
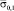
|
СП |
Класс |
αμ |
ασ |
|
Ni |
«Мыши» |
9,98 |
5,01 |
|
«Мулы» |
11,12 |
6,72 |
|
|
«Слоны» |
10,00 |
7,80 |
|
|
Vi |
«Мыши» |
9,99 |
7,35 |
|
«Мулы» |
10,52 |
7,25 |
|
|
«Слоны» |
9,99 |
7,94 |
Из табл. 1−3 видно, что изученные СП вне зависимости от размера окна агрегации τ в разные дни являются СП с ограниченными областями рассеяния, в то время как оценки параметров ФР μ, σ не являются стационарными величинами и могут меняться как по дням недели, так и в течение одного дня.
Из табл. 4 видно, что использованная процедура агрегации СП Ni, Vi не является масштабно-инвариантной по параметру σ, а потому статистические свойства изученных СП оказываются зависящими от размера окна агрегации τ. Данный результат, в свою очередь, позволяет поставить под сомнение правомерность использования для описания изученных СП самоподобных моделей и определяет необходимость анализа значений показателей Херста СП Ni, Vi, результаты которого представлены в следующем разделе.
Анализ показателей Херста накопленных сумм временных рядов Ni, Vi
Оценка показателя Херста СП Ni, Vi осуществлялась в соответствии с алгоритмом HCALC [5], предусматривающим получение оценки значения показателя Херста по зависимости накопленной дисперсии приращений обобщенного броуновского движения от длины приращения. Листинг m-функции, возвращающей значение показателя Херста ВР, вычисленного в соответствии с алгоритмом HCALC, приведен в [15].
В ходе проведенных исследований были вычислены в каждый из дней наблюдений для каждого класса СП Ni, Vi значения показателя Херста по полной последовательности («глобальное» значение показателя Херста) для ранее выбранных значений окон агрегации 0,1 и 1,0 с, а также усредненные по ансамблю, содержащему оценки показателя Херста, вычисленные на девяти непересекающихся частях СП (табл. 5).
При этом использовались следующие параметры алгоритма HCALC:
– длина приращения Pmax = 20;
– число отчетов, по которым осуществляется вычисление накопленной дисперсии, L = 9000 для полного ВР и L = 1000 для частей ВР;
– координата вектора, начиная с которой вычисляется накопленная дисперсия, Nstart = 1 для полного ВР и 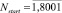 с шагом в тысячу для частей ВР.
с шагом в тысячу для частей ВР.
Также были вычислены средние за весь период наблюдений значения глобальных и усредненных значений показателей Херста СП Ni, Vi (табл. 6).
Из табл. 5, 6 видно, что показатель Херста СП Ni, Vi оказывается некоторой случайной величиной, изменяющейся как в течение недели, так и в течение одного дня. При этом его значения оказываются существенно зависящими от размера окна агрегации, что также является свидетельством, подтверждающим обоснованность отклонения гипотезы о самоподобии СП Ni, Vi.
Напомним, следуя [5], что фрактальным броуновским движением называется гауссовский процесс X(t) c параметром Херста H (0 < H < 1), обладающий следующими свойствами:
1. Х(0) = 0 и функция Х(t) почти всегда непрерывна.
2. Случайная величина
ΔX = X(t2) – X(t1)
имеет нормальное гауссовское распределение с нулевым математическим ожиданием и дисперсией 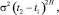 , где t2 > t1, s – положительная константа.
, где t2 > t1, s – положительная константа.
Таблица 5
Показатели Херста СП Ni, Vi в каждый из дней наблюдений (окон агрегации 0,1 и 1 с)
|
День |
Класс |
СП Ni |
СП Vi |
||||||
|
«Глобальный» показатель Херста |
Усредненный показатель Херста |
«Глобальный» показатель Херста |
Усредненный показатель Херста |
||||||
|
0,1 с |
0,1 с |
0,1 с |
1 с |
0,1 с |
1 с |
0,1 с |
1 с |
||
|
1 |
Мыши |
0,645 |
0,903 |
0,636 |
0,896 |
0,926 |
0,980 |
0,911 |
0,973 |
|
Мулы |
0,871 |
0,956 |
0,862 |
0,953 |
0,852 |
0,948 |
0,840 |
0,944 |
|
|
Слоны |
0,923 |
0,975 |
0,902 |
0,967 |
0,936 |
0,981 |
0,915 |
0,974 |
|
|
2 |
Мыши |
0,719 |
0,933 |
0,695 |
0,917 |
0,957 |
0,986 |
0,944 |
0,978 |
|
Мулы |
0,893 |
0,964 |
0,872 |
0,957 |
0,850 |
0,948 |
0,834 |
0,942 |
|
|
Слоны |
0,912 |
0,973 |
0,899 |
0,967 |
0,907 |
0,974 |
0,893 |
0,967 |
|
|
3 |
Мыши |
0,732 |
0,933 |
0,704 |
0,918 |
0,864 |
0,962 |
0,835 |
0,950 |
|
Мулы |
0,856 |
0,962 |
0,848 |
0,956 |
0,810 |
0,945 |
0,814 |
0,943 |
|
|
Слоны |
0,834 |
0,949 |
0,821 |
0,940 |
0,825 |
0,946 |
0,818 |
0,939 |
|
|
4 |
Мыши |
0,672 |
0,919 |
0,661 |
0,911 |
0,828 |
0,949 |
0,801 |
0,942 |
|
Мулы |
0,873 |
0,966 |
0,858 |
0,958 |
0,856 |
0,960 |
0,843 |
0,953 |
|
|
Слоны |
0,883 |
0,967 |
0,867 |
0,961 |
0,879 |
0,967 |
0,864 |
0,961 |
|
|
5 |
Мыши |
0,632 |
0,904 |
0,620 |
0,897 |
0,824 |
0,954 |
0,793 |
0,941 |
|
Мулы |
0,883 |
0,959 |
0,871 |
0,954 |
0,860 |
0,952 |
0,839 |
0,944 |
|
|
Слоны |
0,873 |
0,959 |
0,863 |
0,953 |
0,893 |
0,968 |
0,868 |
0,956 |
|
|
6 |
Мыши |
0,766 |
0,953 |
0,724 |
0,935 |
0,811 |
0,944 |
0,775 |
0,928 |
|
Мулы |
0,885 |
0,965 |
0,864 |
0,951 |
0,852 |
0,956 |
0,835 |
0,944 |
|
|
Слоны |
0,909 |
0,976 |
0,860 |
0,956 |
0,917 |
0,979 |
0,865 |
0,958 |
|
|
7 |
Мыши |
0,667 |
0,921 |
0,646 |
0,908 |
0,784 |
0,938 |
0,758 |
0,923 |
|
Мулы |
0,850 |
0,960 |
0,843 |
0,952 |
0,823 |
0,948 |
0,812 |
0,940 |
|
|
Слоны |
0,874 |
0,963 |
0,858 |
0,953 |
0,873 |
0,964 |
0,862 |
0,956 |
|
Таблица 6
«Глобальные» значения показателя Херста для окон агрегации 0,1 и 1 с
|
Класс |
«Глобальное» значение показателя Херста |
|||
|
СП Ni |
СП Vi |
|||
|
0,1 с |
1 с |
0,1 с |
1 с |
|
|
Мыши |
0,690 ± 0,049 |
0,902 ± 0,062 |
0,856 ± 0,064 |
0,959 ± 0,181 |
|
Мулы |
0,873 ± 0,016 |
0,951 ± 0,029 |
0,843 ± 0,019 |
0,951 ± 0,005 |
|
Слоны |
0,887 ± 0,031 |
0,958 ± 0,024 |
0,890 ± 0,036 |
0,968 ± 0,012 |
В этой связи для объяснения причин обнаруженных случайных изменений значений показателя Херста были изучены статистическиех свойства первых разностей СП Ni, Vi.
Статистические свойства первых разностей временных рядов Ni, Vi
Всего были изучены статистические свойства первых разностей 4200 частичных последовательностей, выбираемых из СП Ni, Vi (3 класса потоков × 2 случайные последовательности (объем информации и кол-во пакетов) × 7 дней × 100 окон агрегации (от 0,1 до 10 с) = 4200). Для каждой частичной последовательности были вычислены первые разности, и для них проверялась статистическая гипотеза о нормальности их распределений с помощью критерия типа Колмогорова – Смирнова и критерия χ2. Далее была составлена бинарная таблица, в которой при принятии статистической гипотезы о нормальности закона распределения частичной СП устанавливалось значение, равное 1 и 0 в противоположном случае. Затем по ней были вычислены относительные доли данного типа частичных последовательностей, для которых гипотеза о нормальности распределения первых разностей была принята. Зависимости относительной доли случайных последовательностей, у которых первые разности имеют нормальный закон распределения 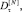
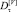 , от размера окна агрегации представлены на рис. 3 и 4.
, от размера окна агрегации представлены на рис. 3 и 4.
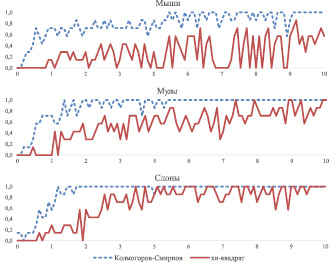
Рис. 3. Зависимости относительной доли 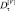 случайных последовательностей, у которых первые разности имеют нормальный закон распределения, от размера окна агрегации
случайных последовательностей, у которых первые разности имеют нормальный закон распределения, от размера окна агрегации
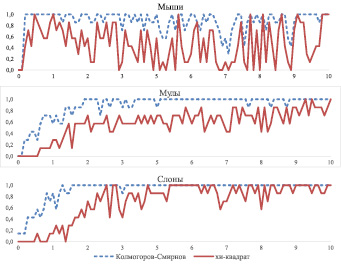
Рис. 4. Зависимости относительной доли 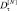 случайных последовательностей, у которых первые разности имеют нормальный закон распределения, от размера окна агрегации
случайных последовательностей, у которых первые разности имеют нормальный закон распределения, от размера окна агрегации
Из рис. 3 и 4 видно, что:
– При применении критерия типа Колмогорова – Смирнова и критерия χ2 зависимости относительных долей 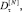
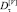 оказываются отличными для различных окон агрегации.
оказываются отличными для различных окон агрегации.
– Гипотеза о нормальном распределении первых разностей изученных частичных последовательностей отвергается, что подтверждает отсутствие самоподобия у изученных зависимостей.
– Наибольшей вариативностью, безотносительно критерия и окна агрегации, обладают зависимости относительных долей 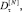
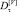 класса «Мыши». Это согласуется с физическими представлениями о формировании сессий информационного обмена данного класса, которые образованы пакетами небольших размеров, имеют короткий период существования, спонтанно появляются и исчезают. Суммарный объем данных, передаваемый такими сессиями, может значительно отличаться в различные моменты времени.
класса «Мыши». Это согласуется с физическими представлениями о формировании сессий информационного обмена данного класса, которые образованы пакетами небольших размеров, имеют короткий период существования, спонтанно появляются и исчезают. Суммарный объем данных, передаваемый такими сессиями, может значительно отличаться в различные моменты времени.
– Классы «Слоны» и «Мулы» имеют меньшую вариативность зависимости относительных долей 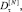
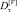 для окон агрегации от 5 с и выше. С точки зрения физического смысла это можно объяснить особенностями формирования сессий информационного обмена данных классов. Так как такие сессии образованы пакетами максимального размера, имеют продолжительный период существования и к ним применяются различные технологии шейпинга (ограничение скорости со стороны провайдера в связи с ограниченной пропускной способностью канала), суммарные объемы данных, передаваемые этими потоками в различные моменты времени, отличаются незначительно.
для окон агрегации от 5 с и выше. С точки зрения физического смысла это можно объяснить особенностями формирования сессий информационного обмена данных классов. Так как такие сессии образованы пакетами максимального размера, имеют продолжительный период существования и к ним применяются различные технологии шейпинга (ограничение скорости со стороны провайдера в связи с ограниченной пропускной способностью канала), суммарные объемы данных, передаваемые этими потоками в различные моменты времени, отличаются незначительно.
– В соответствии с критерием χ2, безотносительно окна агрегации, зависимости относительных долей 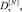
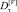 с нормальным законом распределения оказываются отличным от единицы, что подтверждает неправомерность использования самоподобных моделей.
с нормальным законом распределения оказываются отличным от единицы, что подтверждает неправомерность использования самоподобных моделей.
Заключение
Проведено исследование особенностей информационных потоков, проходящих через магистральный интернет-канал, на основе анализа случайных последовательностей, содержащих значения числа пакетов, переданных выделенными типами информационных потоков в течение выбранного временного интервала (Ni), а также объемов переданной информации данным типом информационных потоков в течение выбранного временного интервала (Vi).
Полученные оценки значений показателя Херста случайных последовательностей Ni, Vi и их первых разностей позволяют сделать обоснованный вывод о несоответствии изученных процессов модели фрактального броуновского движения.
Анализ плотностей распределений и выборочных плотностей случайных последовательностей Ni, Vi показал, что для их описания можно использовать модель случайных броуновских блужданий в ограниченной области рассеяния. Напомним, что в рамках данной модели плотность распределения представляется линейной комбинацией функций гауссовского распределения, сдвинутых друг относительно друга. Данный результат позволяет выдвинуть гипотезу о том, что свойствами фрактального броуновского движения могут обладать накопленные суммы случайных последовательностей Ni, Vi. Для подтверждения справедливости данной гипотезы или ее отклонения необходимо, в свою очередь, проверить гипотезу о возможности генерации фрактального броуновского движения в случае использования случайных величин с ограниченной областью рассеяния.
Результаты намеченных исследований являются предметом последующих публикаций.
Библиографическая ссылка
Поршнев С.В., Божалкин Д.А. К ВОПРОСУ О САМОПОДОБИИ ТРАФИКА, ПЕРЕДАВАЕМОГО В МАГИСТРАЛЬНОМ ИНТЕРНЕТ-КАНАЛЕ // Фундаментальные исследования. 2016. № 4-2. С. 301-310;URL: https://fundamental-research.ru/ru/article/view?id=40172 (дата обращения: 04.03.2026).