При проектировании гидравлических регулирующих органов для трубопроводной системы, в которых действие на затвор осуществляется за счет энергии рабочей среды с целью сброса повышенного или поддержания заданного уровня давления, предотвращения обратных протечек, остается актуальной проблема борьбы с нежелательными последствиями эффекта кавитации в потоках жидкости [17]. В частности, к таковым относятся повреждения внутренних поверхностей проточных каналов данных устройств в виде эрозийных кратеров, а также возникающий шум и вибрации в элементах трубопроводной арматуры [8, 18]. Перечисленные факторы влияют на прочностные характеристики данного арматурного оборудования и препятствуют реализации нормальных условий его эксплуатации в рамках нормативных стандартов, в том числе санитарных. Расчет проточной части регулирующих органов связан с оценкой набора критических параметров кавитации, которые, в частности, вводятся в соответствии с числом кавитации κ = 2Eu согласно критерию Эйлера и определяются гидродинамическими и виброакустическими методами [3, 5, 6]. Проявление первичных кавитационных эффектов в пузырчатой форме вызвано резким падением давления жидкости до значений ниже, чем давление ее насыщенного пара (например, при t = 20,8 °С для водяного – pH = 2,5·103 Па [17]), вследствие течения рабочей среды через проточную часть регулирующего органа при дросселировании или изменении направления потока жидкости. Таким образом, описание механизма поведения кавитационных пузырей в процессах их эволюции представляет особый интерес в вопросах проектирования гидравлических регулирующих устройств.
Цель работы – анализ современных методов моделирования основных стадий развития эффекта гидродинамической кавитации.
Краткое понятие о гидродинамической кавитации
Естественная гидродинамическая кавитация [3, 19] – эффект разрыва потока жидкости, который в отличие от акустической кавитации (под воздействием звуковых волн) [21, 31] наблюдается при понижении давления до критических значений в локальной области высокоскоростных течений жидкостной среды. Физическая природа рассматриваемого явления связана также с переходными термодинамическими процессами (от метастабильного к устойчивому состоянию системы) вследствие того, что одновременно с резким понижением давления жидкости происходит ее перегрев. Моделирование течений жидкостных сред в условиях естественной гидродинамической кавитации, возникающей при резком падении давления в процессе обтекания тел различной формы, например в трубопроводных системах при нарушении их герметичности, в насадках, в проточных частях регулирующих органов (в том числе при работе клапана – его закрытии или открытии с расширением потока) и т.д., связано с решением множества задач. К ним можно отнести описание механизмов: образования кавитационной полости, ее расширения, сжатия, схлопывания и др., которые соответствуют начальной и развитой стадиям кавитации.
Современные подходы к моделированию начальной стадии гидродинамической кавитации
А. Стохастический подход. Разделяя процесс формирования указанных полостей в соответствии с гомогенным и гетерогенным механизмами зародышеобразования [25], следует выделить стохастический подход к их описанию: модели гомогенной нуклеации [7, 22, 30, 36]; модификации с введением фактора гетерогенности [12, 23, 26, 29]; модели гетерогенной нуклеации, например, на частицах примесей жидкостной среды [19, 20], на стенке [27, 33], в ее трещинах (впадинах) [16]. Классические работы Я.И. Френкеля [22], который продолжил идеи V. Volmer и A. Weber [36], дополнены исследованиями J.Н. Lienhard и A. Karimi [30] с предложением в теории [22] сравнивать работу, затрачиваемую на формирование критического нуклеона – W* с минимальным значением его потенциальной энергии (без уточнения кинетической энергии молекул). Как уже отмечалось, критический нуклеон представляет собой паровой зародыш в жидкостной среде с метастабильным состоянием. Частота нуклеации J (число зародышей в единичном объеме за единицу времени) определяется формулой [22]
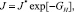
где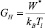 
– число Гиббса; J* – константа, которая зависит от значений коэффициентов – поверхностного натяжения среды и диффузии газа в ней, числа молекул жидкости, их объема; kB – постоянная Больцмана; Tl – температура жидкости. В частности, выражение (1) применяется в модели В.К. Кедринского [7] для расчета полного объема диффузионных слоев Xd и плотности кавитационных пузырей Nd (радиусом R и радиусом диффузионного слоя rd) в единице объема жидкостной среды (вулканической магмы) с помощью кинетических уравнений
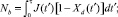
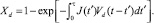(1)
Здесь τ – время нуклеации кавитационных зародышей (период индукции);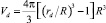 
– объем диффузионного слоя.
Модифицированные модели [26, 27] используются для описания течений жидкостной среды с абразивными частицами малых размеров. При этом гомогенное зародышеобразование может не наблюдаться вследствие более низких значений изменения температуры (например, для воды меньших в десятки раз) в сравнении с перепадами температуры для потоков очищенной жидкости. Модификация для J представляется в виде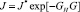 
, где G – фактор гетерогенности, который характеризует степень уменьшения значения работы, затрачиваемой на формирование критического нуклеона. Заметим, что наиболее распространенными являются две формы данного фактора в соответствии с работами Md. Alamgir, J.H. Lienhard [23] и E. Ellas, P.L. Chambre [26]
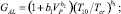
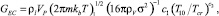(2)
где T10, Tcr – начальное и критическое значения температуры жидкости, К; Vp – скорость падения давления, Па/с; σ – избыточная свободная энергия; ρV, ρl – плотности фаз (пузырька и жидкости); m – молекулярная масса; b1, b2, b3, c1, c2 – константы. Кроме того, имеются работы, учитывающие в рамках модификации [23] теорию гомогенной нуклеации, а также последующее расширение кавитационных полостей за счет межфазного массобмена. Отметим, что авторы исследований [7, 29] выполнили расчеты для флуктуационного зародышеобразования в условиях диффузии газа.
Представляет интерес модель объемной гетерогенной нуклеации, учитывающая распределение гетерогенных ядер по размерам [12], в которой использован подход из [28] для способа учета соответствующего экспериментального распределения (близкого к логнормальному) для частиц примеси кавитирующих потоков жидкости при акустических эффектах. В случае [12] согласно распределениям центров парообразования (в форме нормального, логнормального и равновероятного законов) по радиусам этих частиц N(r) проводится оценка их числа
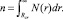
Как отмечается авторами [12, 33], работы S.G. Bankoff [24] и Y.Y. Hsu [27], посвященные соответственно гетерогенной нуклеации на стенке [24] и в ее трещинах [27], заложили основу для дальнейших исследований в данных направлениях. При этом выявлены критерии реализации зародышеобразования: разница свободной энергии объемной нуклеации превышает значение этой величины для пристенной [24]; расширение полусферического пузыря во впадине происходит, если разность значений температур пузырей – указанного и равновесного с тем же радиусом, больше нуля [27]. В частности, T.S. Shin и O.C. Jones [33] предложили эмпирическое соотношение для частоты гетерогенной нуклеации на стенке в виде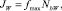 
где при c0 = 104 и c = 2,5·0–8 корреляция частоты отрыва пузырей 
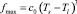нелинейно зависит от разности температур стенки и жидкости, а плотность образовавшихся пузырей 
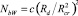определяется их радиусами – при критическом значении Rcr и при отрыве Rd.
Б. Детерминированный подход. Детерминированный подход, применяемый традиционно для описания поведения одиночного кавитационного пузыря, представлен уравнением движения (жидкости около дисперсной сферической частицы переменного радиуса) типа Рэлея – Ламба (Рэлея – Плессета) [16, 19], имеющим различные модификации в зависимости от набора учитываемых эффектов – инерционных, тепловых и диффузионных. Общая постановка краевой задачи со свободной границей, которая представлена в работе Си-Ди-Ю [20], для выделенной поверхности, разделяющей две области: внутреннюю – парогазовую и внешнюю – жидкостную с растворенным газом, обычно переносится на приближение о сферической форме кавитационной полости [16, 19]. При этом указанное уравнение представляет собой обобщение системы уравнений в сферических координатах: неразрывности, движения для несущей фазы, энергетического баланса, теплопроводности, диффузии и условий на межфазной границе. Например, в пренебрежении диффузионными и тепловыми факторами классическое уравнение Рэлея – Ламба
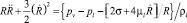(3)
при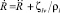 
позволяет проанализировать радиальное движение поверхности сферической полости R(t) в безграничной несжимаемой жидкости вязкостью μl и плотностью ρl с учетом интенсивности фазовых переходов ζlv на указанной поверхности и разности давлений фаз (pv – pl). Отметим, что в настоящем изложении не рассматривается случай сжимаемой жидкости, характерной для акустической кавитации. Отдельный интерес представляют задачи устойчивости сферической формы пузыря.
Поведение кавитационного пузыря на стенке согласно [14, 19] может быть представлено в виде сложного движения (при разложении на радиальное и поступательное) с источником (стоком) в центре и заменой обтекания диполем при направлении его момента вдоль перемещения пузыря. Метод зеркальных отображений позволяет описать суммарный потенциал течения двух симметричных диполей и двух фиктивных источников, применяемый для расчета кинетической энергии выделенной системы. Система уравнений Лагранжа II рода в обобщенных координатах (для радиуса пузыря и расстояния от его центра до стенки) позволяет оценить скоростные режимы роста кавитационной полости у стенки.
В. Комбинированный подход. Известен традиционный метод моделирования течений системы жидкость – пар – газ, как гетерогенной с двумя фазами («несущей» – жидкости и «дисперсной» – совокупности пара и газа) в форме континуумов, подчиняющихся законам сплошной среды, обобщенным Р.И. Нигматулиным [16]. При этом реализуется составление системы характерных уравнений в пространственно-временных переменных Эйлера, когда искомые функции, например скорость потока, задается в каждой точке пространства и имеет смысл ее субстанциональная производная по времени. Активно развивается другой способ моделирования движения указанных сред, когда несущая фаза – континуум (в переменных Эйлера), а дисперсная – образует совокупность частиц, положение которых задается переменными Лагранжа – координатами в выбранной системе отсчета в данный момент времени [12, 15, 34]. При этом в зависимости от точности предлагается искомые функции для каждой фазы отыскивать при решении систем уравнений для каждой фазы в отдельности с последующим уточнением влияния межфазных массовых, импульсных и энергетических переносов. В рамках задач описания кавитационных течений помимо детерминированных уравнений сохранения массы, импульса и энергии можно привлечь стохастический подход, например, к анализу частоты нуклеации или оценке изменения радиуса пузырей. В частности, в работе [12] введение концентрации пузырьков пара (в том числе, при гетерогенной нуклеации на стенке и в объеме), дополненное уравнением состояния воды в виде условия Тэта приводит к замыканию эйлеровского этапа моделирования. При этом уравнение Рэлея – Ламба на лагранжевом этапе дополняется законами сохранения массы и внутренней энергии. Аналогичный способ моделирования, но с применением теории гомогенного зародышеобразования использован в работах [15].
Основные способы описания развитой гидродинамической кавитации
В теоретическом плане остается проблемным описание переходного этапа от начальной к развитой стадии гидродинамической кавитации, в то время как задачи об устойчивости развитой каверны имеют давнюю историю. Вопросы исследования механизма частичного замыкания каверны на теле (например, при движении крыльев, винтов, вращениях симметричных объектов и т.д.) обычно рассматриваются с позиций искусственной кавитации (суперкавитации) [10, 11], когда замыкание кавитационной полости на теле с помощью дополнительного вдувания воздуха становится полным, т.е. завершается за телом при скоростях потока, много меньших, чем для развитых стадий естественной кавитации. Экспериментальные данные о форме каверны свидетельствуют об образовании в области ее замыкания струйки, которая нарушает целостность хвостовой части кавитационной полости и формирует ее парогазовый след. Как правило, в этих случаях используется метод теории струй, распространяющий реальное течение среды на конформное отображение с помощью искомой преобразующей функции, которая задается различными способами. Известны схемы расчетов плоских течений: Кирхгоффа, Жуковского – Рошко, Рябушинского, Т. Ву, Д.А. Эфроса, два представления М. Тулина и их модификации [19]. Однако в настоящей работе ограничимся изложением подходов с возможным их применением к явлению гидродинамической кавитации в проточных частях регулирующих органов трубопроводов, т.е. в случае эволюции пузырчатой кавитации.
Согласно обзору [11] cтепень эрозийного влияния развитой кавитации на рабочие поверхности различных гидродинамических устройств определяется двумя факторами соответственно вследствие несимметричного и симметричного схлопывания кавитационной полости: формированием кумулятивной струйки вблизи стенки (или при обтекании тела) с последующим возможным гидроударом [4, 9, 32]; возникновением сферических ударных волн [2]. Например, в работе [31] выполнена оценка скорости указанной струйки при обтекании тела одиночной каверной, которая позволяет рассчитать давление кумулятивного течения на поверхность тела. Численное исследование направления развития струйки вблизи наклонной стенки проведено в [4]. Моделирование высокоскоростной ударной струи в форме цилиндрического столба жидкости, действующей на изотропное упругое полупространство, после схлопывания кавитационного пузыря представлено в работе [1]. Автор [2] применяет уравнения Лагранжа II рода при описании сложного движения одиночной каверны с разложением на радиальное и поступательное движения и применяет метод конформных отображений. Работа A. Thiruvengadam [35] содержит расчетные формулы для интенсивности кавитационной эрозии, а также относительного размера ядра в зависимости от критериев Вебера, Маха и числа кавитации. Описание схлопывания пузырей связано с задачами акустической кавитации [21, 31], в частности, при использовании аппроксимаций Кирвуда – Бете для движения поверхности полости с учетом сжимаемости жидкости [13].
Заключение
Итак, начальная стадия развития гидродинамической кавитации согласно опытным данным [3, 8, 18, 19] разделяется на паровую (в разрывных полостях), газовую (при расширении нуклеонов – газовых зародышей) и парогазовую. Кроме того, возможна диффузия газа сквозь стенки паровых полостей и два вида зародышеобразования: гомогенная (флуктуационная для паровой фазы в жидкости без примесей) и гетерогенная (для системы газ - пар взвешенных частицах примесей, стенках и их трещин) [25]. В развитой стадии сжатие и схлопывание полостей наблюдается тем быстрее, чем меньше содержание газа в их объеме вследствие конденсации пара на фазовой границе при шумовых эффектах и гидроударе с обтекаемых тел. Существенное содержание газа в системе пар-газ приводит к пульсациям каверны из-за возможного адиабатического сжатия воздуха с повышением температуры (до значений порядка 103 °С) и свечением [8, 18, 19]. Анализ известных литературных источников выявил применение стохастического, детерминированного подходов и их комбинаций на этапе описания начальной стадии гидродинамической кавитации. Однако дифференциальные распределения зародышей кавитации по их радиусам, используемые в известных моделях, постулируются на основе опытных данных. При исследовании развитой стадии используется детерминированный подход с применением метода теории струй.
Библиографическая ссылка
Капранова А.Б., Лебедев А.Е., Мельцер А.М., Неклюдов С.В., Серов Е.М. О МЕТОДАХ МОДЕЛИРОВАНИЯ ОСНОВНЫХ СТАДИЙ РАЗВИТИЯ ГИДРОДИНАМИЧЕСКОЙ КАВИТАЦИИ // Фундаментальные исследования. 2016. № 3-2. С. 268-273;URL: https://fundamental-research.ru/ru/article/view?id=40043 (дата обращения: 17.05.2025).