Проанализированная динамика развития учебной кафедры технического университета (УКТУ) показывает, что кафедра нуждается в современной и достаточно сложной системе управления. В работе [1] приводится обоснование необходимости введения для УКТУ автоматизированной системы поддержки управления.
Для успешного функционирования и развития кафедры необходимо четкое представление выделяемых ресурсов по каждой предстоящей задаче. Причем некоторые из этих задач будут взаимосвязанными, а потому будет присутствовать корреляция между затраченными на них ресурсами, а порою они будут взаимодополняющими, в результате чего будет проявляться эффект диверсификации. Стоит учесть, что в начале года нет и не может быть четкого, полного списка задач для кафедры – существует высокая вероятность, что произойдут различные изменения. Поэтому задача прогнозирования необходимых ресурсов и их распределения отнюдь не является простой. Она обязана учитывать дополнительные вероятные факторы нагрузки и будет являться сложно-ситуационной задачей. Из-за сложного характера взаимосвязей между задачами УКТУ нет возможности провести линейную оценку каждой составляющей, а затем линейно вычислить общий итог через ассоциативность входящих компонент – необходимо учитывать все внутренние взаимосвязи и пользоваться нелинейным моделированием.
Рассмотрим процесс подготовки специалистов в области ИТ заданного государственным стандартом уровня компетентности в качестве некоторого производственного процесса, который имеет определенные задачи, ресурсы для их решения и соответствующие регламенты управления. Однако при постановке конкретной задачи редко оцениваются необходимые ресурсы конкретно для этой задачи, и нет оценки того, как повлияет выполнение задачи (или процесс выполнения задачи) на подготовку выпускников. Обычно считается, что ресурсов хватить должно или они откуда-нибудь появятся. Если уже на момент выполнения задачи выясняется, что ресурсов недостаточно, тогда формулировка задачи начинает меняться.
Инструменты, которые фактически оценивают ресурсный потенциал УКТУ на текущий момент, используют данные, полученные на основании уже произошедших событий и заблаговременно заложенных в бюджетный план деятельности кафедры. Это не позволяет делать обоснованных вероятностных прогнозов на изменение ситуации в будущем. В книге [3] представлено преимущество динамических моделей над статистическими срезами показателей в конкретные моменты времени.
Порою при возникновении новых проектов, какими бы срочными и необходимыми они ни оказались, приходится ждать достаточно долгое время, требуемое для согласования этого проекта через бухгалтерию с другими инстанциями, выделяющими финансирование под соответствующие проекты. Порою такое согласование может затянуться, из-за чего некоторые задачи могут уже стать неактуальными. Для бурно развивающейся ИТ-индустрии такие проволочки крайне нежелательны и губительны. Поэтому необходим иной подход в оценке возможностей кафедры к будущему развитию. Такому подходу соответствует разработанный комплекс по прогнозированию необходимых для УКТУ ресурсов [2].
Для построения адекватного прогноза по необходимым УКТУ ресурсам важно иметь полное представление о системе функционирования кафедры, реально оценивать начальные ресурсы, которыми она обладает, представлять взаимодействия УКТУ с другими подразделениями, учитывать ее возможные задачи на ближайший год. При помощи математических и логических связей все входные параметры могут быть учтены в одной управляющей функции. Для упрощения составления этой функции все входные параметры стоит разбить на несколько блоков [2]. Этими основными блоками будут являться:
- Финансовый блок (F).
- Нормативный блок (N).
- Оборудование (O).
- Персонал (P).
- Обучаемые студенты (S).
Чтобы выделить все существенные переменные в каждом из блоков и неявные зависимости между выделенными блоками, целесообразно внутри каждого блока осуществить более мелкий кластерный анализ. После выделения переменных и межблочных зависимостей можно составить функционал для оценки эффективности использования ресурсов кафедры:
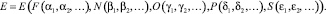(1)
Аргументы функций, входящих в указанный функционал (1), являются частными подблоками каждого из рассматриваемых блоков. Они описываются в работе [7] достаточно подробно. В работе [6] обосновывается возможность и необходимость параметризации каждого из аргументов через единый финансовый параметр.
Тогда (1) принимает вид
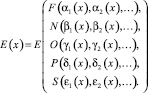(2)
Такой подход в значительной степени упрощает программную реализацию модели, но привносит трудности в математическую составляющую (из-за появления дополнительного параметра). Также при данном подходе появляется необходимость в использовании экспертных оценок, т.к. далеко не все переменные в блоках очевидным образом выражаются через финансовый параметр (например, многие элементы блоков P и S). На выходе модель будет давать количественный результат.
Из-за динамичности всех рассматриваемых данных и присутствия в них скрытых взаимосвязей задача получения оценки для такого функционала не является очевидной. Если не получить в достаточном объеме достоверных статистических данных и вывести зависимости между блоками, а также между входящими в их состав кластерами, будет невозможно получить корректный результат по всей кафедре в целом. Для определения зависимостей и связей между блоками логично ввести корреляционную матрицу, значения которой будут рассчитываться на основании имеющейся статистики и экспертных оценок. Организованные таким образом данные будут зависимы между собой и не будут статичными.
При учете корреляций между входящими данными и учете эффекта диверсификации в затратах ресурсов на разные задачи получится, с одной стороны, учитывать изменение тенденций в выделяемых ресурсах на смежные задачи, а с другой стороны, не учитывать повторно одинаковые показатели сразу в нескольких блоках.
При решении задачи по оценке максимальной эффективности кафедры возникает оптимизационная задача, целью которой является нахождение наилучшего (с точки зрения какого-то критерия, далеко не единственного) распределения ожидаемых ресурсов. Сформулирована она может быть следующим образом:
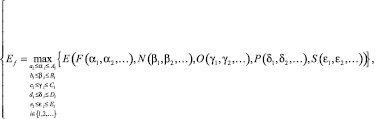(3)
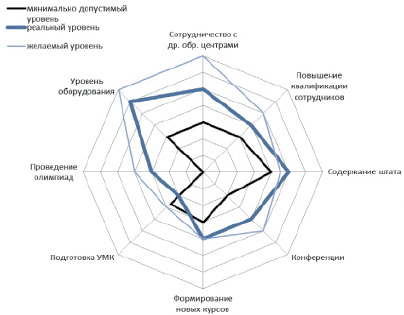
Графическое представление направлений работы кафедры
В формулировке (3) указаны ограничения (законодательные, материальные, людские), которые накладываются на каждый из рассматриваемых блоков. При этих заданных ограничениях и будет решаться задача наилучшего распределения ресурсов для достижения максимальной эффективности по выбранному критерию. Критерии могут быть совершенно различными: от минимизации расходов кафедры при сохранении необходимого уровня функциональности до максимизации функциональности при условии непревышения порогового уровня допустимых затрат.
Наглядно задачу можно представить при помощи лепестковых диаграмм. Для этого строится разложение функционирования нашей кафедры по выбранным в кластерном анализе базисным элементам. Дополнительно проводится разложение по этим же элементам минимального допустимого уровня функционирования кафедры и желаемого при конкретно выбранном критерии эффективности. На рисунке изображена полученная таким путем диаграмма.
При таком представлении задач кафедры описываемая в работе задача может сводиться:
I. К одновременной минимизации площади, образованной из-за превышения уровня графика «желаемого уровня» над «реальным», и стремлении к нулю площади, образованной из-за превышения уровня графика «минимально допустимого» над «реальным».
II. К одновременной максимизации площади, образованной из-за превышения уровня графика «реального уровня» над «минимально допустимым», и стремлении к нулю площади, образованной из-за превышения уровня графика «минимально допустимого» над «реальным».
Теперь проведем доказательство разрешимости построенного таким образом функционала и, как следствие, возможности построения оговоренной модели не только для одной конкретно взятой кафедры, но и индуктивное ее расширение на другие области. Для адекватности предположим наличие достаточных статистических данных и предварительно оценим адекватность самого построения модели с математической точки зрения.
С математической точки зрения стратегия разбиения на блоки полностью определяется функциями дележа риска. Общая идея доказательства предложена в работе [5].
Пусть риск по взятому отделенному подмодулю описывается функцией g(X). Учитывая ресурсные затраты на другие задачи, пусть ресурсы, которые можно выделить под конкретно выбранный подмодуль, будут обозначены cre(t) = cre(g(Xt)).
Ресурсы УКТУ в момент времени t ≥ 0, с учетом возможных спонсорских поддержек, обозначим R(t):
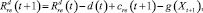
где d – средний размер постоянных расходов.
Резервы в начальный момент времени совпадают с начальными ресурсами: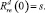 
С практической точки зрения логично учесть дополнительные ограничения на вероятность невыполнения УКТУ своих взятых обязательств (чтобы минимизировать этот расчетный параметр в дальнейшей модели), рассматривая ее деятельность на конечном горизонте планирования T. Если момент такого разорения
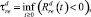
то вероятность нехватки ресурсов на решения поставленных задач выражается
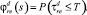
Дополнительно ограничим вероятность невыполнения обязательств с помощью квантильного критерия Value-at-Risk, предварительно выбрав уровень доверительного интервала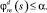 
Мерой рентабельности будем считать суммарные дисконтированные отчисления на постоянные расходы, проводимые согласно стратегии d(t) к моменту времени T с учетом возможного покрытия спонсорской поддержкой, а также ограничениями на вероятность перехода в нерентабельное состояние:
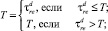
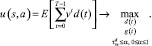
Для решения поставленной оптимизационной задачи запишем уравнение Гамильтона - Якоби:
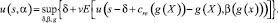
при следующем наборе ограничений:
0 ≤ δ ≤ s;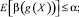 
0 < g(X) ≤ X.
Тройка (δ* = δ*(s, a); β*(x) = β*(s, a, x); g*(x) = g*(s, a, x)) является максимизатором в уравнении Гамильтона – Якоби [4] и определяет решение поставленной оптимизационной задачи.
Для дальнейшего анализа решения поставленной оптимизационной задачи воспользуемся рекурсивным представлением функции
u0(s, α) = 0;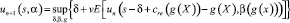 
при ограничениях поставленной задачи.
В рамках выделенных рекурсивных обозначений при n ≥ 0, 0 < α ≤ 1, s ≥ 0:
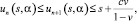
где с – изначальные ресурсы с учетом возможно одобренных спонсорских поддержек (и до выделения под другие задачи).
Доказательство проведем по индукции:
u0(s, α) ≤ u1(s, α);
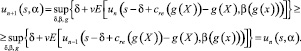
При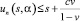 
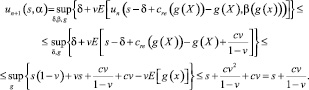
Тем самым мы доказали, что un(s, α) является неубывающей последовательностью функций, ограниченных сверху.
Докажем теперь, что существует решение, и оно единственное, для приведенного уравнения Гамильтона - Якоби.
По доказанному имеем, что un(s, α) является ограниченной сверху неубывающей последовательностью функций, а следовательно, существует функция, являющаяся поточечным пределом для un(s, α):
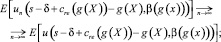
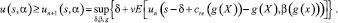
С другой стороны, из un(s, α) ≤ u(s, α) следует, что
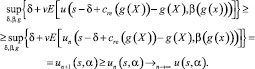
Значит,
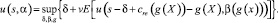
Тем самым доказана разрешимость поставленной оптимизационной задачи. Значит, при достаточном объеме статистических данных построенная таким образом модель способна делать прогнозы о необходимых ресурсах для дальнейшего развития и функционирования УКТУ.
Библиографическая ссылка
Томашевский С.В. ОПТИМИЗАЦИОННАЯ ЗАДАЧА ПРОГНОЗИРОВАНИЯ НЕОБХОДИМЫХ КАФЕДРЕ РЕСУРСОВ // Фундаментальные исследования. – 2016. – № 3-1. – С. 56-61;URL: https://fundamental-research.ru/ru/article/view?id=40005 (дата обращения: 14.10.2024).