Вопросы теплопереноса при сварке трением с перемешиванием (СТП) представляют большой интерес как с точки зрения теории, так и практики. В процессе СТП температура в зоне сварки и ее распределение по металлу существенным образом влияют на скоростные и технологические характеристики, а также на процессы массопереноса и фазовые превращения. Рассматриваемый метод относится к способам сварки материалов в твердой фазе, где скорость диффузионных процессов, обеспечивающих надежное соединение свариваемых деталей, очень сильно зависит от температуры в области сваривания.
Большинство работ, посвященных расчету распределения температуры в процессе СТП и её динамики, основаны на решении уравнения теплопроводности [2, 4, 7]. Для решения этого уравнения авторами используются различные численные методы, реализуемые в виде компьютерных программ. В частности, авторы работы [3] моделируют трехмерное температурное поле образца с учетом поступательного движения инструмента СТП, представляющего собой вращающийся твердосплавный пин с заплечником.
Применение результатов этих теоретических работ в практике СТП сопряжено с рядом затруднений. Первое из них заключается в необходимости численного решения трехмерной (в некоторых случаях двумерной) задачи для уравнения теплопроводности, что требует разработки специального комплекса программ с высокими требованиями к вычислительным возможностям компьютера. Второе состоит в необходимости учета в уравнении теплопроводности тепловых потерь на излучение и конвективный теплообмен с окружающей средой. Третье затруднение связано с падением подводимой тепловой мощности при приближении температуры в области вращающегося пина к температуре плавления металла из-за уменьшения вязкости. При этом также возрастает удельная теплоемкость свариваемых материалов. Это приводит к зависимости граничных условий задачи и коэффициентов уравнения теплопроводности от искомого температурного поля и резко усложняет модель температурной динамики в СТП.
Математическая модель температурной динамики СТП
Компьютерные расчеты температурной динамики при СТП с учетом тепловых потерь и падения подводимой мощности предлагается проводить на основе следующей упрощенной модели. Рассмотрим металлический образец (заготовку) в форме диска с толщиной h, малой в сравнении с радиусом диска. Это позволяет пренебречь изменениями температуры в направлении, перпендикулярном плоскости диска. В приближении нулевой скорости поступательного движения пина относительно образца принимается также, что подводимая в центре диска теплота распространяется аксиально-симметрично.
В процессе сварки теплота выделяется в области контакта с материалом заготовки вращающегося инструмента, рабочая часть которого состоит из узкого наконечника (пина) и более широкого диска (заплечника). Пин инструмента рассматривается приближенно в виде узкого цилиндра с радиусом r0 (рис. 1, а). Частично теплота выделяется в тонкой цилиндрической области образца у поверхности пина. Некоторая часть теплоты выделяется на плоской поверхности образца в области контакта с заплечником. Подводимая к вращающемуся инструменту механическая мощность преобразуется главным образом в тепловую мощность. В стационарном режиме сварки выделяющаяся в образце тепловая мощность PG практически не зависит от времени, если не учитывать уменьшение вязкости материала при повышении температуры образца в области тепловыделения. В нестационарных режимах тепловая мощность является также функцией времени P(t), определяемой в основном технологическим режимом. Необходимо также учитывать, что часть выделяющейся теплоты отводится от образца непосредственно через инструмент. Соответствующая доля зависит как от материала свариваемого образца, так и самого инструмента. Обычно доля отводимой тепловой мощности через инструмент составляет от 15 до 25 % от общей выделяемой мощности [9, 10]. Поэтому в предлагаемой модели температурной динамики образца принимается значение тепловой мощности, равное P = αPG, где α – коэффициент, значения которого в зависимости от материала образца лежат в интервале 0,75–0,85 [6, 8]. Выделяющаяся в процессе сварки теплота мощностью P распространяется с течением времени в радиальном направлении диска. Этот процесс сопровождается зависящей от температуры потерей энергии с открытой его поверхности.
Составим систему дифференциальных уравнений математической модели динамики температурного поля образца. Для этого мысленно выделим вокруг центрального цилиндра (пина) с радиусом r0 концентрические цилиндрические поверхности с нелинейно возрастающими радиусами r1, r2, ... rN (рис. 1, б). Величина r1 принимается равной радиусу заплечника. Радиус rN внешней цилиндрической поверхности равен внешнему радиусу диска. Таким образом, свариваемый образец оказывается разделенным на N относительно узких кольцевых элементов. Важной особенностью модели является то, что ширина кольцевых элементов последовательно увеличивается от центра диска к периферии по мере уменьшения температурного градиента. Это позволяет упростить математическую модель, существенно уменьшив число уравнений, описывающих энергетический баланс каждого кольцевого слоя, ограниченного указанными цилиндрическими поверхностями.
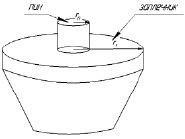
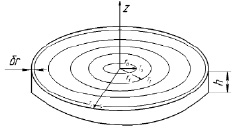
а б
Рис. 1. Инструмент для СТП (а) и схема выделения кольцевых элементов диска (б)
Пространственная дискретизация аксиально-симметричного температурного поля осуществляется так. За температуру k-го кольца (k = 0, 1, ... N – 1) принимается величина абсолютной температуры Tk на цилиндрической поверхности с радиусом rk.
Энтальпия кольца является функцией температуры и выражается как
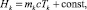 (1)
(1)
где с – удельная изобарная теплоемкость металла; mk – масса k-го кольца. Скорость изменения энтальпии для выделенного k-го кольца можно представить в виде уравнения энергетического баланса:
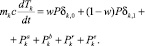 (2)
(2)
Здесь w – доля мощности, выделяющейся в области контакта с образцом пина, от величины P мощности, идущей на нагрев образца. Остальная ее часть выделяется в области контакта с заплечником. 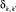 – дельта-символ Кронекера. Масса k-го кольца связана с его размерами и плотностью металла r соотношением
– дельта-символ Кронекера. Масса k-го кольца связана с его размерами и плотностью металла r соотношением
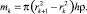 (3)
(3)
Слагаемые 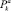 и
и 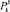 в правой части уравнения (2) представляют собой количества теплоты, получаемой за единицу времени соответственно от (k – 1)-го и (k + 1)-го кольца в результате теплопередачи. В соответствии с законом теплопроводности получаем для них выражения
в правой части уравнения (2) представляют собой количества теплоты, получаемой за единицу времени соответственно от (k – 1)-го и (k + 1)-го кольца в результате теплопередачи. В соответствии с законом теплопроводности получаем для них выражения
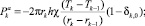 (4)
(4)
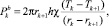 (5)
(5)
где c – теплопроводность металла. Положительные значения этих величин отвечают поступлению, а отрицательные – потере энергии k-м кольцом. Мощность потери энергии кольца на тепловое излучение как абсолютно серого тела равна
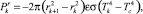 (6)
(6)
где ε – коэффициент поглощения излучения металлом; σ – постоянная Стефана – Больцмана; Tc – температура окружающей среды (воздуха). Мощность, теряемая поверхностью кольца из-за конвективного теплообмена с окружающим воздухом, представлена в уравнении (2) последним слагаемым, равным
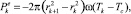 (7)
(7)
где w – коэффициент теплоотдачи металл - воздух.
Подставив выражения (3)–(7) в уравнение (2), описывающее энергетический баланс кольцевого элемента образца, получаем после преобразований уравнение динамики температуры k-го элемента в виде
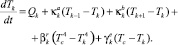 (8)
(8)
При значениях k = 0, 1, ... (N – 1) получаем систему N уравнений (8) температурной динамики кольцевых элементов образца, коэффициенты которой определяются следующими формулами:
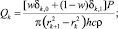 (9)
(9)
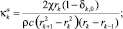 (10)
(10)
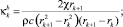 (11)
(11)
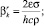
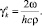 (12)
(12)
Система уравнений (8) не является замкнутой, так как не определено уравнение динамики температуры TN на торце диска. Поэтому выделяем у этой поверхности столь тонкое кольцо толщиной δr (δr << (rN – rN–1)), что можно ограничиться учетом потерь энергии на излучение и конвективную теплоотдачу только через торцевую поверхность образца. Уравнение энергетического баланса такого элементарного кольца запишем в виде
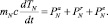 (13)
(13)
Масса элемента выражается так:
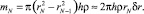 (14)
(14)
Опираясь на формулы (5)–(7), раскрываем слагаемые в правой части уравнения (13). В результате получаем уравнение динамики температуры торцевой поверхности диска:
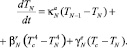 (15)
(15)
Коэффициенты правой части этого уравнения выражаются так:
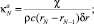
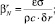
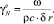 (16)
(16)
Таким образом, система из N + 1 уравнений (8) и (15) является замкнутой. Решение этой системы при заданных N + 1 начальных значениях температуры Tk(0), где k = 0, 1, ... N, определяет зависимость от времени температуры кольцевых элементов.
Коэффициенты математической модели
Коэффициенты системы уравнений (8) и (15), выражаемые формулами (9)–(12) и (16), определяются геометрическими параметрами образца, физическими свойствами его материала и технологическими условиями СТП. Поэтому они могут быть зависимыми как от времени, так и от локальной температуры образца.
Генерируемая в результате трения инструмента и образца тепловая мощность и ее часть, идущая в образец, даже при стационарном режиме СТП могут изменяться в процессе сварки по мере изменения температуры в области контакта. Из-за уменьшения вязкости с ростом температуры тепловая мощность снижается. Особенно заметно проявляется это при приближении температуры к точке плавления материала. Поэтому для приближения математической модели СТП к реальному процессу в формуле (9) вводимую в образец тепловую мощность P будем описывать функцией температуры T0 контактирующего с пином кольцевого элемента:
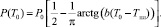 (17)
(17)
Здесь Tпл – температура плавления материала образца; b – подгоночная постоянная. Значение b подбирается так, чтобы расчетные характеристики были наилучшим образом согласованы с экспериментальными данными для данного металла. Приемлемые значения этой постоянной лежат обычно в интервале (0,05–0,15 К–1). Вид кривых функции зависимости вводимой мощности и ее производной по температуре в области, примыкающей к пину, показан на рис. 2. Температура плавления соответствует точке плавления алюминиевого сплава АД31. Видно, что при достижении температуры плавления металла вводимая мощность в сварное соединение при СТП стремится к нулю.
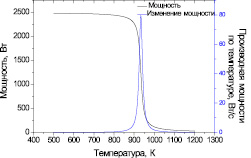
Рис. 2. Зависимость вводимой мощности и ее производной по температуре
От температуры материала зависит также и удельная теплоемкость. При фазовых переходах вещества, в частности при плавлении, происходит скачкообразное изменение энтальпии, равное по величине теплоте перехода. Это приводит к зависимости изобарной теплоемкости от температуры с δ-образным пиком в точке плавления. Поэтому удельную изобарную теплоемкость c, которая входит в коэффициенты системы уравнений (8) и (15), моделируем функцией температуры k-го элементарного кольца вида
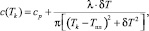 (18)
(18)
где cp – удельная изобарная теплоемкость твердой фазы; l – удельная теплота плавления δT – ширина интервала температуры, в котором происходит плавление металла.
На рис. 3 приведена рассчитанная по формуле (18) кривая зависимости от температуры удельной теплоемкости алюминиевого сплава АД31 в области плавления.
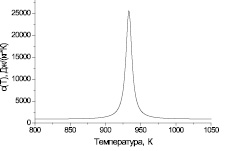
Рис. 3. Зависимость от температуры удельной теплоемкости сплава АД31
Численное моделирование динамики температурного поля СТП
Полученная выше система дифференциальных уравнений (8) и (15) моделирует динамику аксиально-симметричного дискретизированного температурного поля образца-диска при СТП в условиях, когда источник тепла неподвижно фиксирован в центре диска.
В процессе вращения инструмента СТП тепловая мощность генерируется как в области, примыкающей непосредственно к узкому пину, так и под относительно широким заплечником. Литературные данные по технологии СТП указывают на то, что суммарная мощность разделяется примерно следующим образом: около 30 % выделяется около пина, а 70 % - у рабочей поверхности заплечника [6, 10]. Поэтому в формуле (9) принимаем значение коэффициента w = 0,3.
Кольцевые элементы образца в рассмотренной модели разделяются концентрическими поверхностями с возрастающими радиусами. Как было отмечено выше, r0 – радиус пина, а значение r1 надлежит взять равным радиусу заплечника. Возрастающие радиусы остальных цилиндрических поверхностей могут быть выбраны достаточно произвольным образом, так чтобы радиус rN совпадал с габаритным радиусом торцевой поверхности. Практика расчетов показывает, что отношение текущего радиуса к предыдущему рационально выбрать в пределах от 1,4 до 2,0. Число кольцевых элементов N в интервале 7–10 вполне достаточно для применения рассматриваемой модели в решении технологических задач.
Величина вводимой тепловой мощности P0 зависит как от материала образца, так и от его толщины h. В частности, для алюминиевого сплава АД31 толщиной h = 5 мм для обеспечения технологически обоснованной скорости СТП достаточной является величина вводимой мощности P0 = 2500 Вт.
Моделирование динамики температурного поля при СТП проводилось для следующих материалов: сталь 12Х18Н10Т; алюминиевый сплав АД31; медный сплав М3; титановый сплав ВТ-6. Необходимые для численных расчетов значения теплофизических характеристик материалов, включая коэффициент поглощения теплового излучения e. Их значения были взяты из справочников [1, 5] и приведены в табл. 1. Данные по значениям коэффициента w конвективной теплоотдачи металл - воздух имеют значительный разброс, вызванный различием в условиях проведения эксперимента. Поэтому рассматриваем w в качестве подгоночного параметра модели, приемлемые значения которого определяются путем сопоставления моделируемой температурной динамики остывания образца с экспериментальной. Такие значения также отражены в табл. 1.
Таблица 1
Теплофизические характеристики материалов для моделирования процесса теплопереноса при СТП
|
Сталь 12Х18Н10Т |
Алюминиевый сплав АД31 |
Медный сплав М3 |
Титановый сплав ВТ-6 |
|
|
Плотность, ρ (кг/м3) |
7,8·103 |
2,71·103 |
8,9·103 |
4,5·103 |
|
Удельная теплоемкость, c (Дж/кг·К) |
447 |
880 |
390 |
540 |
|
Удельная теплота плавления, λ (Дж/кг) |
82·103 |
390·103 |
205·103 |
358·103 |
|
Теплопроводность, c (Вт/м·К) |
45,4 |
209,3 |
389,6 |
21,9 |
|
Температура плавления, Tq (К) |
1823 |
933,32 |
1357,6 |
1668 |
|
Коэффициент поглощения материала, ε |
0,185 |
0,075 |
0,32 |
0,64 |
|
Коэффициент теплоотдачи металл - воздух ω (Вт/м2·К) |
13 |
13 |
13 |
13 |
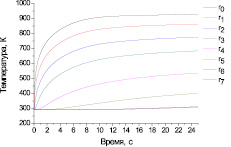
Рис. 4. Зависимость температуры кольцевых элементов от времени для сплава АД31
Динамика дискретизированного температурного поля образца описывается решением системы из N + 1 уравнений (8) и (15) при заданных начальных значениях температуры кольцевых элементов Tk(0), где k = 0, 1, ... N. Для решения такой задачи можно воспользоваться пакетами математических программ, имеющими встроенные функции решения системы дифференциальных уравнений. К таким пакетам, обладающим также возможностями графической визуализации, относятся, например, Mathcad, Maple и др. Результаты данной работы были получены в среде Mathcad-14.
Зависимости от времени температуры кольцевых элементов диска из алюминиевого сплава толщиной 5 мм и габаритным радиусом 160 мм при вводимой тепловой мощности 2500 Вт приведены на рис. 4. Начальные их температуры приняты равными температуре среды Tc = 290 К. Радиусы элементов приняты равными: 3; 5; 7; 10; 20; 40; 80; 160 мм, при N = 7. Время задавалось с шагом 0,01 с в интервале от 0 до 120 с.
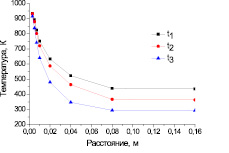
Рис. 5. Радиальное распределение температуры для диска из алюминиевого сплава: в моменты времени t1 = 12 с, t2 = 60 с и t3 = 120 с
Температура СТП составляет 0,8–0,9 от температуры плавления Tq. Из расчетных кривых на рис. 4 видно, что в области сваривания (r ≤ r0) такая температура достигается примерно за 2–3 с. Отсюда можно оценить скорость СТП в пределах от 1 до 1,5 мм/с.
На рис. 5 приведены кривые радиальной зависимости температуры образца для моментов времени t = 12; 60 и 120 с.
Из анализа кривых на рис. 5 видно, что в течение нескольких первых секунд вводимая мощность приводит в основном к увеличению температуры в области сваривания. В последующие интервалы времени сообщаемая энергия идет преимущественно на нагрев образца за пределами области сваривания.
Математическая модель температурной динамики СТП, представленная системой уравнений (8) и (15), применима к широкому спектру материалов. Это открывает возможности для сравнения технологических параметров СТП различных сплавов. Для образцов с рассмотренными выше геометрическими параметрами и теплофизическими характеристиками, отраженными в табл. 1, произведены расчеты зависимости от времени температуры кольцевых элементов. Их результаты для элементов с внутренним радиусом r1, следующим за заплечником, приведены на рис. 6. Вводимая мощность P0 = 2500 Вт.
Из сравнения кривых на рис. 6 можно сделать вывод о том, что наибольшая скорость увеличения температуры области сваривания у образца из титанового сплава ВТ-6, а наименьшая – у образца из меди (М3). У образцов из стали и алюминия значения скорости нагрева имеют промежуточные значения.
Режим остывания. Сравнение с экспериментом
Моделирование температурной динамики в режиме остывания также осуществляется численным решением системы уравнений (8) и (15) при условии нулевой мощности нагрева (P0 = 0). Начальные температуры кольцевых элементов Tk(0), где k = 0, 1, ... N, принимаются равными их конечным значениям, полученным в режиме нагрева.
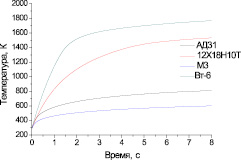
Рис. 6. Зависимость от времени температуры второго элемента (r1) для различных сплавов
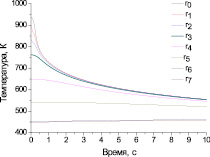
Рис. 7. Процесс остывания элементов алюминиевого образца с радиусами rk
Процесс остывания образца из алюминиевого сплава АД31Т был исследован экспериментально. Температуры кольцевых элементов с внутренними радиусами r1 и r4 измерялись методом термопар с использованием тензометрической станции А17-Т8 и самописца. Термопара представляла собой хромель-алюмелевую проволоку диаметром 0,25 мм. Термопары крепили на поверхность металлического образца зачеканкой на расстоянии 5 и 20 мм от оси ввода тепла. Измерения повторялись трижды и учитывались средние значения температур.
Расчетные кривые зависимости от времени температуры кольцевых элементов r1 и r4 в режиме остывания изображены на рис. 7. Здесь же показаны экспериментальные значения температуры этих элементов с интервалом в 1 с.
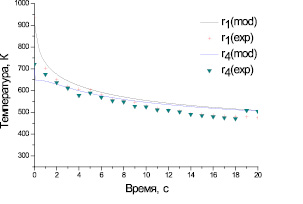
Рис. 8. Зависимость от времени температуры кольцевых элементов (r1 и r4) алюминиевого образца АД31 в режиме остывания: r1(mod) и r4(mod) – расчетные кривые; r1(exp) и r4(exp) – экспериментальные точки
Сравнение расчетных и экспериментальных зависимостей на рис. 8 показывает, что рассматриваемая математическая модель температурной динамики вполне пригодна для описания СТП в приближении неподвижного источника нагрева. Расхождение расчетных и экспериментальных значений температуры не превышает 5 % во всем интервале времени.
Выводы
Разработана относительно простая математическая модель температурной динамики СТП в приближении неподвижного инструмента (пина с заплечником), расположенном в центре образца-диска. Она представлена системой уравнений (8) и (15), которые при заданных начальных значениях температуры могут быть численно решены с помощью известных компьютерных программ. Учитываются тепловые потери на излучение и конвективную теплоотдачу.
Эта модель позволяет оперативно решить ряд технологических задач. В частности, при заданных мощности тепловыделения, размерах и теплофизических характеристиках деталей или образцов можно оценить скорость СТП. Возможно сравнение технологических параметров СТП для различных материалов. Модель также описывает температурную динамику образца в условиях его остывания.
Библиографическая ссылка
Рзаев Р.А., Чуларис А.А., Джалмухамбетов А.У., Атуев Ш.М. ДИНАМИЧЕСКАЯ МОДЕЛЬ РАСПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ В МЕТАЛЛЕ ПРИ СВАРКЕ ТРЕНИЕМ С ПЕРЕМЕШИВАНИЕМ // Фундаментальные исследования. 2016. № 3-1. С. 47-55;URL: https://fundamental-research.ru/ru/article/view?id=40004 (дата обращения: 05.01.2026).



