В работах [2, 4, 8] предложена математическая модель застреливания строительных элементов в грунт из многоствольных откатных артиллерийских орудий [5]. Разработка математических моделей для решения основной задачи внутренней баллистики [6] таких орудий является актуальной в связи с необходимостью проектирования строительных пушек и оценки эффективности их применения для решения задач гражданской практики [1, 8]. При принятии решения о возможности использования математической модели для решения основной задачи внутренней баллистики, прежде всего, важно изучить вопросы об устойчивости модели относительно входных параметров и верифицировать модель на основе натурных экспериментов, так как только адекватная модель может быть применена на практике. Такую математическую модель можно, прежде всего, использовать для проведения однопараметрического численного анализа, используемого при изучении свойств многоствольного артиллерийского орудия.
Математическая модель импульсного вдавливания строительных элементов в грунт
Введем следующие обозначения: n – количество стволов в многоствольном орудии, каждый ствол имеет свой порядковый номер i, где 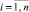 ; υa и La – абсолютные скорость и путь сваи (строительного элемента) в грунте; m – масса строительного элемента; Qi – вес откатных частей пушки с номером i; Lp,i – путь отката откатных частей пушки с номером i; Mi – масса откатных частей пушки с порядковым номером i в многоствольной системе; q – вес строительного элемента; t – время; Vi – скорость откатных частей пушки с номером i; pi – давление пороховых газов в канале i-го ствола; Si – площадь поперечного сечения i-го ствола; θi – показатель адиабаты пороховых газов без единицы; Ψi – относительная часть сгоревшего заряда в стволе i;
; υa и La – абсолютные скорость и путь сваи (строительного элемента) в грунте; m – масса строительного элемента; Qi – вес откатных частей пушки с номером i; Lp,i – путь отката откатных частей пушки с номером i; Mi – масса откатных частей пушки с порядковым номером i в многоствольной системе; q – вес строительного элемента; t – время; Vi – скорость откатных частей пушки с номером i; pi – давление пороховых газов в канале i-го ствола; Si – площадь поперечного сечения i-го ствола; θi – показатель адиабаты пороховых газов без единицы; Ψi – относительная часть сгоревшего заряда в стволе i; 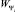 – свободный объем каморы к моменту сгорания в ней части заряда Ψi; F(υa, La) – сила сопротивления грунта движению в нем строительного элемента; Gi(Vi, Lp,i) – сила сопротивления откату для пушки с номером i.
– свободный объем каморы к моменту сгорания в ней части заряда Ψi; F(υa, La) – сила сопротивления грунта движению в нем строительного элемента; Gi(Vi, Lp,i) – сила сопротивления откату для пушки с номером i.
Рассмотрим математическую модель многоствольного откатного артиллерийского орудия, приведенную в работах [2, 4, 8], при следующих условиях: сила сопротивления грунта движению застреливаемого строительного элемента F(υa, La) удовлетворяет соотношению
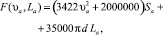
где Sa – площадь миделевого сечения строительного элемента [1], а силы сопротивления откату при выстреле Gi(Vi, Lp,i) равны нулю.
Для этих условий решение основной задачи внутренней баллистики многоствольного орудия описывается следующими уравнениями.
Предварительный период выстрела для каждого из стволов описывается известной формулой внутренней баллистики:
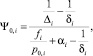
где 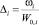 – плотность заряжания; ωi, W0,i, δi, fi, p0,i, αi – масса заряда, объем каморы, плотность пороха, сила пороха, давление форсирования, коволюм пороховых газов в стволе i.
– плотность заряжания; ωi, W0,i, δi, fi, p0,i, αi – масса заряда, объем каморы, плотность пороха, сила пороха, давление форсирования, коволюм пороховых газов в стволе i.
На основе уравнения Резаля, геометрического закона горения пороха и законов классической механики получены уравнения, описывающие первый период выстрела в каждом стволе:
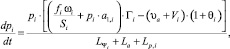 (1)
(1)
где 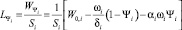 – приведенная длина каморы в i-м стволе,
– приведенная длина каморы в i-м стволе, 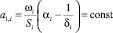 ;
; 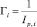 – удельная интенсивность газообразования; Ip,i – импульс пороха в i-м стволе.
– удельная интенсивность газообразования; Ip,i – импульс пороха в i-м стволе.
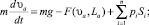 (2)
(2)
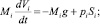 (3)
(3)
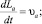 (4)
(4)
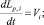 (5)
(5)
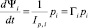 (6)
(6)
Начальные условия для решения системы уравнений (1)–(6) имеют вид
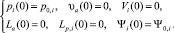 (7)
(7)
Второй период выстрела каждого ствола предлагается описывать следующими уравнениями:
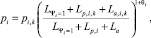 (8)
(8)
где 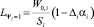 , pi,k – давление в стволе i в конце первого периода выстрела; Lp,i,k – величина отката ствола i в конце первого периода выстрела; La,i,k – абсолютный путь поршня в конце первого периода выстрела для ствола i.
, pi,k – давление в стволе i в конце первого периода выстрела; Lp,i,k – величина отката ствола i в конце первого периода выстрела; La,i,k – абсолютный путь поршня в конце первого периода выстрела для ствола i.
Очевидно, что второй период выстрела для ствола i описывается системой уравнений (2)–(5), (8).
Начальные условия для этой системы уравнений имеют вид
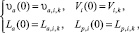 (9)
(9)
где υa,i,k – абсолютная скорость строительного элемента в конце первого периода в стволе i; Vi,k – скорость отката ствола i в конце первого периода выстрела, La,i,k, Lp,i,k – абсолютный путь строительного элемента и откаты стволов в конце первого периода выстрела.
Во время выстрела многоствольной строительной артиллерийской системы первый и второй периоды выстрела могут заканчиваться и начинаться в разные моменты времени соответственно. Поэтому расчеты с помощью приведенных уравнений внутренней баллистики нужно выполнять согласно правилу: если для орудия i выполняется условие Ψi(t) < 1, то для описания внутрибаллистических процессов решается задача Коши (1)–(7). Если Ψi(t) = 1 и Lp,i + La ≤ Ld,i, то решается задача Коши (2)–(5), (8)–(9), где Ld,i – длина канала ствола i. Если Lp,i + La > Ld,i, то давление pi(t) ≡ 0.
Очевидно, что после выхода поршня из всех каналов стволов движение сваи в грунте описывается задачей Коши:
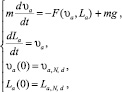 (10)
(10)
где N – номер ствола, из которого поршень вышел последним; υa,N,d, – абсолютная скорость поршня в момент его выхода из канала ствола N; La,N,d – абсолютный путь поршня по каналу ствола в суммарное время первого и второго периодов выстрела.
Очевидно, что величина проникания строительного элемента в грунт соответствует значению La, при котором выполняется равенство υa = 0.
Легко видеть, что при выполнении условия n = 1 приведенные выше системы уравнений описывают динамику выстрела из одноствольного орудия [3, 9].
Исследование математической модели и результаты однопараметрического анализа
Согласно работам И.Г. Русяка и В.М. Ушакова для решения задач Коши, описанных выше, можно использовать метод Рунге – Кутты 2-го порядка с шагом интегрирования 10–6 с [6]. Для численного решения основной задачи внутренней баллистики многоствольных откатных орудий и расчета проникания строительных элементов в грунт были использованы специально разработанные на языке Delphi 7 программы для персональных компьютеров, совместимых с IBM PC и функционирующих в операционных системах версий не ниже Windows XP [7].
Таблица 2
Показатели преимущества импульсного вдавливания по сравнению со свободным застреливанием для многоствольных откатных орудий
|
Параметр |
Количество стволов в системе |
|||||
|
3 |
4 |
5 |
||||
|
ИВ |
СЗ |
ИВ |
СЗ |
ИВ |
СЗ |
|
|
Величина проникания, м |
1,70 |
1,17 |
1,88 |
1,26 |
2,30 |
1,35 |
|
Относительное увеличение проникания при ИВ по сравнению со СЗ, % |
34,5 |
– |
39,1 |
– |
70,4 |
– |
Примечание. Способы застреливания: ИВ – импульсное вдавливание, СЗ – свободное застреливание.
Численные эксперименты показали устойчивость математической модели относительно технических характеристик стволов, входящих в многоствольную систему, и условий их заряжания. Так отклонение исходных параметров модели на 1 % повлекло отклонение результатов решения основной задачи внутренней баллистики многоствольных орудий на величину не более 3 %.
Проведенный однопараметрический анализ для трехствольной системы позволил сделать выводы, приведенные в табл. 1.
Таблица 1
Результаты однопараметрического анализа для трехствольной системы (изменение величины проникания строительного элемента в грунт, максимальных давлений в стволах, дульных скоростей откатов стволов при увеличении параметра)
|
Параметр |
L |
Номера стволов |
|||||
|
1 |
2 |
3 |
|||||
|
p1, max |
V1 |
p2, max |
V2 |
p3, max |
V3 |
||
|
Масса заряда в стволе 2 |
– |
↓ |
↓ |
↑ |
↑ |
↓ |
↓ |
|
Импульс пороха в стволе 2 |
↓ |
↑ |
↑ |
↓ |
↓ |
↑ |
↑ |
|
Объем каморы в стволе 2 |
↓ |
↑ |
↑ |
↓ |
↓ |
↑ |
↑ |
|
Калибр ствола 2 |
↓ |
↓ |
– |
↓ |
– |
↓ |
– |
|
Масса ствола 2 |
– |
– |
↓ |
– |
↓ |
– |
↓ |
|
Масса строительного элемента |
↑ |
↑ |
↑ |
↑ |
↑ |
↑ |
↑ |
|
Диаметр строительного элемента |
↓ |
– |
↑ |
– |
↑ |
– |
↑ |
Примечание. Обозначения: L – проникание строительного элемента в грунт; ↑ – величина увеличивается; ↓ – уменьшается; «–» – исследование не проводилось либо однозначной зависимости нет.
Полученные выводы основаны на анализе графических зависимостей, отображающих результаты выполненных численных экспериментов.
Численное исследование изменения основных внутрибаллистических зависимостей от количества стволов многоствольной артсистемы позволяют сформулировать следующие выводы, что при увеличении количества стволов, входящих в артиллерийскую систему:
– уменьшаются максимальные давления в каждом из стволов и дульные скорости свободного отката;
– увеличивается проникание застреливаемого строительного элемента в грунт.
Численные эксперименты показали, что с увеличением количества стволов в системе увеличивается эффективность импульсного вдавливания строительных элементов в грунт, при котором строительный элемент перед выстрелом упирается в грунт, по сравнению со свободным застреливанием, при котором строительный элемент входит в грунт после полного выхода всех частей поршня из каналов стволов. Этот вывод основан на результатах расчетов проникания строительных элементов диаметром 0,4 м в глину с консистенцией 0,3, приведенных в табл. 2.
Верификация математической модели для одноствольных орудий [6, 9] показала, что средняя относительная погрешность между экспериментальными и расчетными заглублениями строительных элементов в глинистый грунт с консистенцией 0,3 составила 3,1 % при дисперсии 8,0 %, а средняя относительная погрешность между экспериментальными и расчетными максимальными давлениями в канале ствола во время выстрела составила 2,6 % при дисперсии 5,4 %.
Заключение
Таким образом, можно сделать вывод о том, что согласно проведенным натурным экспериментам для одноствольных откатных орудий, давшим хороший результат верификации соответствующей модели, являющейся частным случаем общей математической модели многоствольных откатных орудий, адекватность общей математической модели многоствольных орудий подтверждается для случая одноствольных откатных пушек.
Исследование математической модели многоствольной артиллерийской системы относительно входных параметров на основе численных экспериментов показало ее устойчивость. Таким образом, предложенную математическую модель можно использовать для описания динамики импульсного вдавливания строительных элементов в грунт из многоствольных откатных артиллерийских орудий.
Работа выполнена при финансовой поддержке Министерства образования и науки РФ (научно-исследовательская работа № 2096 в рамках базовой части государственного задания № 2014/153 в сфере научной деятельности).
Библиографическая ссылка
Остапенко Е.Н. ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ИМПУЛЬСНОГО ВДАВЛИВАНИЯ СТРОИТЕЛЬНЫХ ЭЛЕМЕНТОВ В ГРУНТ ИЗ МНОГОСТВОЛЬНЫХ ОТКАТНЫХ АРТИЛЛЕРИЙСКИХ ОРУДИЙ // Фундаментальные исследования. 2016. № 3-1. С. 42-46;URL: https://fundamental-research.ru/ru/article/view?id=40003 (дата обращения: 26.12.2025).



