Тот факт, что текущая стоимость американской валюты по отношению к рублю зависит от цены на нефть, никем не подвергается сомнению. В экспорте России нефть и продукты ее переработки составляют львиную долю. Прибыль от этого бизнеса поступает в бюджет, соблюдение которого самым непосредственным образом влияет на состояние экономики, а значит, и курс национальной валюты. Вместе с тем взаимодействию курса доллара с ценами на нефть, как и многим большим и сложным экономическим системам, присуще свойство инерционности, состоящее в том, что при изменении цен на нефть курс доллара меняется не мгновенно, а с некоторым запаздыванием (лагом). Регрессионные модели, содержащие в своем составе лаговые переменные, называются динамическими. Целью данной работы является построение динамической регрессионной модели курса доллара к рублю в зависимости от цены на нефть. Динамические модели являются, во-первых, хорошим средством прогнозирования изучаемых явлений, а во-вторых, при наличии инерционности исследуемых процессов часто позволяют избавиться от такого негативного явления, как автокорреляция ошибок регрессии.
Исходные данные
В работе [1] авторы уже проводили исследование зависимости курса доллара США y от цены на нефть марки Brent x по статистическим данным за период с 1 января 2015 г. по 16 октября 2015 г. Информация о курсе доллара была взята в интернет-журнале [4], и она полностью соответствует данным Центрального банка Российской Федерации (ЦБ РФ) [8], а информация о ценах на нефть – с финансового портала [7], и она соответствует данным Межконтинентальной биржи (Intercontinental Exchange, ICE) [6]. В результате была построена динамическая модель:
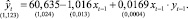 (1)
(1)
Под уравнением регрессии записаны мелким шрифтом: стандартная ошибка оценки y (слева) и стандартные отклонения соответствующих коэффициентов регрессии (справа). Для модели (1) коэффициент детерминации R2 = 0,964, а средняя ошибка аппроксимации E = 1,408 %.
Повторно проведенный авторами анализ полученных результатов позволил установить, что при построении модели (1) не было учтено одно очень важное обстоятельство, связанное с механизмом установления курса доллара ЦБ РФ. Согласно информационно-правовому порталу [5], с 15 апреля 2003 года для установления официального курса доллара используется средневзвешенное значение курса доллара США на торгах Единой торговой сессии межбанковских валютных бирж со сроком расчета «завтра», сложившееся по состоянию на 11 часов 30 минут дня торгов. Это означает, что курс доллара на сегодня устанавливается ЦБ РФ днем раньше, поэтому в модели (1) зависимая переменная yt фактически является курсом доллара вчера, т.е. y t–1. Получается, что модель (1) представляет собой зависимость вчерашнего курса доллара от позавчерашнего курса и вчерашних, а не позавчерашних, цен на нефть.
Помимо неучтенного механизма установления курса доллара ЦБ РФ при построении модели (1) использовались наблюдения в праздничные и выходные дни, в которые курс доллара ЦБ РФ остается постоянным, а цена на нефть изменяется. Это обстоятельство также искажает оценки коэффициентов динамической регрессии.
Таким образом, проведенный анализ позволил выявить неточности, которые были допущены при сборе данных о курсе доллара и ценах на нефть. В результате были собраны новые данные за период с 12.01.2015 по 27.11.2015 г. в будние дни (итого 230 наблюдений). Данные о курсе доллара взяты с сайта ЦБ РФ [8], а данные о ценах на нефть с финансового портала [7]. При этом данные о курсе доллара были «сдвинуты» на один день назад. Все значения курса доллара y за данный период попадают в отрезок от 49,178 до 70,746 рублей, а значения цен на нефть x – от 42,69 до 67,77 долларов за баррель.
Анализ переоцененной по новым данным динамической модели
Оцененная по новым данным динамическая модель имеет вид
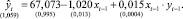 (2)
(2)
Коэффициент детерминации R2 = 0,967, ошибка аппроксимации E = 1,368 %. Как видно, качество модели (2) стало немного выше, чем у регрессии (1).
Предположим, что цены на нефть стабилизировались и не меняются во времени, т.е. в регрессии (2) переменная x t–1 = const. Обозначим a = 67,073 – 1,020x t–1, b = 0,015x t–1. Тогда модель (2) будет соответствовать авторегрессионному процессу первого порядка AR(1):
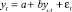 . (3)
. (3)
Авторегрессионные процессы могут быть стационарными и нестационарными. Известно, что авторегрессионный процесс является стационарным тогда и только тогда, когда все корни его характеристического уравнения больше единицы по абсолютной величине [2]. Для процесса (3) характеристическое уравнение имеет вид
1 – bz = 0 или 1 – 0,015x t–1z = 0,
где z – некоторое число (корень характеристического уравнения). Таким образом, стационарность процесса (3) будет зависеть от того, какое значение принимают цены на нефть x t–1. Используя условие стационарности 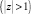 , получим неравенство
, получим неравенство 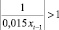 . Решением этого неравенства, в силу неотрицательности цен на нефть, является интервал 0 < x t–1 < 66,667. Это означает, что процесс (2) является стационарным, если цена на нефть будет менее 66,667 долларов. Такой результат можно объяснить тем, что для моделирования использовались статистические данные о ценах на нефть в диапазоне от 42,69 до 67,77, т.е. отсутствует информация о том, что произойдет, если нефть будет выше 67,77 долларов.
. Решением этого неравенства, в силу неотрицательности цен на нефть, является интервал 0 < x t–1 < 66,667. Это означает, что процесс (2) является стационарным, если цена на нефть будет менее 66,667 долларов. Такой результат можно объяснить тем, что для моделирования использовались статистические данные о ценах на нефть в диапазоне от 42,69 до 67,77, т.е. отсутствует информация о том, что произойдет, если нефть будет выше 67,77 долларов.
Вычислим математическое ожидание процесса (2):
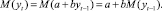
Если процесс стационарный, то M(yt) = M(y t–1), следовательно,
M(yt) = a + bM(yt1).
Из этого равенства
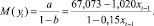 (4)
(4)
График функциональной зависимости математического ожидания курса доллара от цены на нефть (4) для процесса (2) представлен на рис. 1.
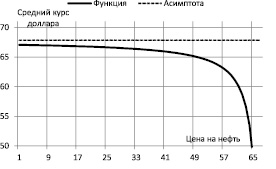
Рис. 1. Зависимость среднего значения курса доллара от цены на нефть для модели (2)
График на рис. 1 демонстрирует ряд недостатков модели (2). Во-первых, эту модель можно использовать на практике только при ценах на нефть, не превышающих порога в 66,667 долларов. Во-вторых, при ценах на нефть в пределах от 60 до 66,667 долларов, находясь «на грани» стационарности, курс доллара может и вовсе оказаться равным 0. В-третьих, график функции имеет горизонтальную асимптоту y = 68, вследствие чего курс доллара при ценах на нефть ниже 40 долларов оказывается примерно одинаковым и равным 68 рублей, чего не может быть в реальности. Подводя итоги, отметим, что динамическую модель (2) можно использовать на практике в узком диапазоне цен на нефть в пределах от 40 до 60 долларов. Для улучшения свойств этой модели и для придания ей более реалистичного экономического смысла была поставлена задача выбрать спецификацию модели регрессии так, чтобы график функции математического ожидания курса доллара имел не горизонтальную, а наклонную асимптоту.
Модификации динамической модели
Для того чтобы график функции имел наклонную асимптоту, в структуру модели (2) был добавлен регрессор 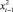 . Динамическая модель приняла следующий вид:
. Динамическая модель приняла следующий вид:
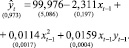 (5)
(5)
Коэффициент детерминации R2 = 0,972, ошибка аппроксимации E = 1,226 %. Модель (5) также описывает авторегрессионный процесс первого порядка AR(1). Исследование процесса показывает, что он является стационарным в интервале 0 < x t–1 < 62,784.
Математическое ожидание процесса (5):
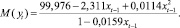 (6)
(6)
Для функции (6) наклонная асимптота имеет вид y = 99,979 – 0,718x t–1, т.е. если цена на нефть приблизится к нулю, то курс доллара составит в среднем примерно 100 рублей. Безусловно, с одной стороны, наличие наклонной асимптоты усиливает практическую значимость модели (5) по сравнению с регрессией (2). Но, с другой стороны, модель (5) стала более ограниченной в применимости.
До сих пор мы сначала оценивали параметры динамической модели, а затем по ней получали зависимость математического ожидания курса доллара от цены на нефть. Пойдем в обратном направлении. Сначала на основе функции (6) оценим нелинейную модель вида
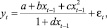
где εt – ошибки модели, которые нужно минимизировать.
Для оценивания нелинейной модели был использован эконометрический пакет Gretl. В качестве начального приближения оценок взяты значения a = b = c = d = 1. В результате была получена зависимость среднего курса доллара от цены на нефть:
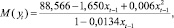 (7)
(7)
в соответствие которой можно поставить уравнение регрессии
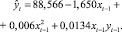 (8)
(8)
График функциональной зависимости математического ожидания курса доллара от цены на нефть (7) для процесса (8) представлен на рис. 2.
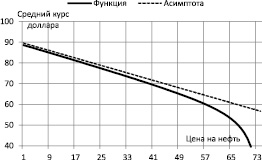
Рис. 2. Зависимость среднего значения курса доллара от цены на нефть для модели (8)
|
Модель |
SP |
R2 |
E |
Ограничение |
|
(2) |
59,574 |
0,967 |
1,368 % |
x t–1 ≤ 60 |
|
(5) |
7,275 |
0,972 |
1,226 % |
x t–1 ≤ 60 |
|
(8) |
2,664 |
– |
1,320 % |
x t–1 ≤ 67 |
|
«завтра будет так же, как сегодня» |
5,413 |
– |
– |
– |
Процесс (8) является стационарным в интервале 0 < x t–1 < 74,627, т.е. менее всего ограничен в применимости по сравнению с моделями (2) и (5). Для модели (8) средняя ошибка аппроксимации E = 1,320 %. Наклонная асимптота для функции (7) имеет вид y = 89,524 – 0,450x t–1.
Предсказание курса доллара по динамическим моделям
Согласно [2], необходимо различать понятия «предсказание» и «прогноз». При предсказании исследователь ограничивает период выборки так, чтобы у него остались несколько последних наблюдений, тогда как при прогнозировании отсутствует какая-либо информация о будущих значениях исследуемых переменных. Для предсказания мы специально оставили 18 наблюдений о курсе доллара и ценах на нефть за период с 30.11.2015 по 23.12.2015. Для каждой модели (2), (5) и (8) были найдены предсказанные значения и рассчитаны ошибки предсказания, равные разности между предсказанными и фактическими значениями. Помимо этого вычислены ошибки для предсказания курса доллара по принципу, что завтрашний курс будет таким же, как сегодняшний. В таблице для каждой модели приводится значение суммы квадратов ошибок предсказания SP, коэффициента детерминации R2, средней ошибки аппроксимации E, а также ограничение на стоимость нефти.
Как видно из таблицы, самыми сильными прогностическими свойствами обладает модель (8), потому что имеет наименьшую из всех регрессий сумму ошибок предсказания (2,664). По диапазону применимости среди динамических моделей лучшей также является регрессия (8). По средней ошибке аппроксимации модели отличаются друг от друга незначительно, поэтому, обобщая вышесказанное, можно сделать вывод, что в практических целях лучше всего использовать модель (8).
Выводы
1. Анализ полученной в работе [1] динамической модели позволил выявить неучтенные ранее особенности в исходных статистических данных о курсе доллара и ценах на нефть, на основе чего была сформирована новая корректная выборка.
2. По новой выборке переоценены параметры динамической модели и проведен её анализ, позволивший установить, что такая регрессия достаточно сильно ограничена в применимости на практике и не соответствует экономическому смыслу задачи.
3. Проведена модификация динамической модели двумя способами, позволившая устранить несоответствие экономическому смыслу задачи прогнозирования курса доллара при малых ценах на нефть.
4. По разработанным динамическим моделям проведено предсказание курса доллара. Лучший результат показала модель (8).
Библиографическая ссылка
Базилевский М.П., Гефан Г.Д. ДИНАМИЧЕСКАЯ МОДЕЛЬ КУРСА ДОЛЛАРА США В ЗАВИСИМОСТИ ОТ ЦЕНЫ НА НЕФТЬ // Фундаментальные исследования. 2016. № 3-1. С. 9-13;URL: https://fundamental-research.ru/ru/article/view?id=39997 (дата обращения: 01.02.2026).



