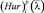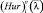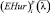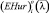Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Фошин Д.В. 1

---

1 ФГОБУ ВО «Финансовый университет при Правительстве Российской Федерации»

Рассматривается задача выбора оптимального инвестиционного проекта в производственной компании. Проанализирован критерий Гурвица для решения матричных игр. Рассмотрены минусы критерия, приводится теоретическая справка по обобщенному критерию Гурвица. Решение проводится с помощью математической модели «Игра с природой», в которой оптимальность стратегий определяется обобщенным критерием Гурвица. Сознательным игроком является отдел инвестиционного анализа компании PepsiCo. Его стратегии заключаются в выборе того или иного продукта для производства. Стратегии бессознательного игрока (природы) определяются в соответствии с курсом рубля к доллару. Выигрыши платежной матрицы определяются как разница между рассчитанным доходом от реализации нового продукта и издержками на его производство. Приводится решение задачи и выводы относительно оптимального выбора инвестиционного проекта.

Статья в формате PDF

565 KB

производственная компания

инвестиционный проект

теория игр

игра с природой

обобщенный критерий гурвица

1. Лабскер Л.Г., Бабешко Л.О. Игровые методы в управлении экономикой и бизнесом. – М.: Дело, 2001, 464 с.

2. Лабскер Л.Г. К вопросу о математической формализации выбора коэффициентов обобщенного критерия Гурвица // Управление риском. – 2009. – № 3 (51). – С. 4–62.

3. Лабскер Л.Г. О показателе оптимизма лица, принимающего решение по обобщенному критерию Гурвица // Экономические науки. – 2009. – № 53 (Апрель). – С. 305–312.

4. Лабскер Л.Г. Обобщенный критерий пессимизма-оптимизма Гурвица // Качество информационных услуг: сб. научных трудов. – Вып. III. – Тамбов, ТГТУ, 2000. – С. 34–43.

5. Лабскер Л.Г. Обобщенный критерий пессимизма-оптимизма Гурвица // Финансовая математика: коллективная монография. – М.: МГУ им. М.В. Ломоносова, 2001. – С. 401–414.

6. Лабскер Л.Г. Теория критериев оптимальности и экономические решения: монография. – М.: КНОРУС, 2014. – С. 742–744.

7. Методические рекомендации по оценке эффективности инвестиционных проектов (утв. Минэкономики РФ, Минфином РФ, Госстроем РФ 21.06.1999 N ВК 477).

8. Экспорт котировок МосБиржа валютный рынок USDRUB_TOM URL: http://www.finam.ru/profile/mosbirzha-valyutnyj-rynok/usdrubtom-usd-rub/export/ (дата обращения: 01.10.15).

9. Hurwicz L. Optimality Criteria for Decision Making under Ignorance // Cowles commission papers. – 1951. – № 370.

10. PepsiCo Снэки | PepsiCo Россия URL: http://www.pepsico.ru/brands/snacks/ (дата обращения: 01.10.15).

Для оценки инвестиционных проектов используется немало методов, существует немало формул, как простых, так и очень сложных. Однако большинство этих формул обладает следующим свойством – пользоваться ими (проводить расчеты) можно только в том случае, если показатели точно известны. К сожалению, никогда нельзя совершенно точно сказать, как пойдет то или иное дело, сколько будет продано товара и как потенциальные потребители отнесутся к его появлению на рынке. Многие экономисты-практики выдвигают вполне обоснованные критические замечания в отношении некоторых существующих методов.

Оценка инвестиционного проекта происходит на этапе, когда как минимум одна из сторон еще не приняла решения о вступлении в своеобразную «игру» – участвовать ли в бизнесе или нет. Задача оценки – доказать, что участие отвечает интересам субъекта и принесет экономическую выгоду. Анализируются возможные последствия проекта, но ключевое слово здесь «возможные», ведь, как уже было сказано выше, невозможно объективно оценить еще не реализованный проект.

Конечно, на данном этапе можно положиться на уже имеющиеся данные по похожим примерам. Однако на эту информацию нельзя полагаться в полной мере: участники, их цели и интересы, непредсказуемая внешняя среда – все это может быть разным.

Кроме того, стоит учитывать и ошибки, возникающие при сборе и анализе данных человеком, а не машиной, хотя и она может дать сбой. Оценка проекта опирается на имеющуюся информацию, а на самом деле ее достоверность зачастую очень сложно проверить. Поэтому проекты подвергаются тщательной экспертизе, но и после нее часть значений могут оставаться в интервальной форме: даже сами разработчики проекта могут понимать, что величины легко смогут принять значение «от» и «до», причем показатели могут отличаться в разы. При разработке проекта учитывается большое количество технических, экономических, технологических и других параметров, определение которых необходимо для понимания свойств и особенностей функционирования инвестиционного объекта [7]. Многие из этих параметров могут не быть измеримы на момент оценки по следующим причинам:

они зависят от будущего (например, от погодных условий, курса валют и др.);

они относятся к прошлому, и эти данные еще не были собраны.

Соответственно, возникает необходимость изучения этой неопределенности. При оценке проекта просто необходимо введение в расчеты вероятности наступления той или иной ситуации – всегда возможны сбои, аварии, природные бедствия, незапланированная реакция рынка и многое другое. Разумеется, эти вероятности необходимо тщательно обосновать и описать.

Ни один инвестиционный проект не застрахован от наступления этих рисков. Более того, один и тот же проект может быть реализован в разных условиях и иметь кардинально разные результаты. Собственно, неопределенность – это неполнота и/или неточность сведений об условиях проведения проекта. А риск, соответственно, вероятность возникновения условий, которые вызовут негативные последствия.

Зачастую статистика и теория вероятностей используется для нахождения показателей, которые можно предсказать «усредненно». Однако в экономике слишком часто процессы единичны – не повторялись и не будут. Следовательно, ограничиваются и возможности строгого применения вероятностных методов [7].

Итак, в оценке инвестиционных проектов необходимо действовать в условиях неопределенности – несколько сторон, имеющих свои цели (или не имеющих – как в случае, например, со стихиями), зависят от действий других сторон. Научно обоснованные способы решения подобных ситуаций дает теория игр. Ее математический аппарат очень широк и позволяет решать многие важные задачи.

По большей части при анализе инвестиционной деятельности возникают ситуации, связанные с играми с природой («статистическими играми»). В этих играх принимают участие два игрока, один из которых старается осознанно принимать эффективные для себя решения – его называют «статистиком», а другой – природа, который не являясь ни союзником, ни противником статистика, принимает случайным образом то или иное свое состояние, не преследуя конкретной цели и абсолютно безразлично к результату игры. Считается, что множество состояний природы заведомо известно, а вероятность наступления того или иного состояния природы может быть определена, а может быть и нет.

Данные игровые модели все чаще применяются в экономике, например, для выбора оптимального поведения фирмы, для рационального управления финансами, теории инвестирования и др. Однако пока что для оценки эффективности проектов они применяются не так часто, как могли бы.

Рассмотрим следующую экономическую ситуацию в производственной компании PepsiCo.

По сравнению с другими странами в России у PepsiCo недостаточно развит сегмент снэков[1]. Правильные инвестиции в эту сферу бизнеса компании могли бы повысить финансовые показатели.

Задача компании – выбор снэкового брэнда для расширения коллекции.

На данный момент в снэковом бизнесе PepsiCo 3 бренда: Lay’s, Cheetos, ХрусTeam [10]. Лучше всех продается Lay’s: он дольше всего на рынке, и в его продвижение вложены колоссальные средства. Два других бренда незначительно уступают ему в продажах. По статистике ряда предыдущих лет уровень спроса по брендам распределяется следующим образом: Lay’s – 0,96, Cheetos – 0,91, ХрусTeam – 0,83. Числовые значения приведены как процент от максимально возможного дохода 1, который компания PepsiCo может получить при реализации произведенного продукта в полном объеме.

Затраты на производство по брендам так же варьируются в зависимости от используемого сырья и технологий: Lay’s – 0,55, Cheetos – 0,5, ХрусTeam – 0,43 от максимально возможного дохода 1, который компания PepsiCo может получить при реализации произведенного продукта в полном объеме.

По данным информационного ресурса Finam рассмотрим курс валюты за год с 31.08.2014 по 31.08.2015 и разделим изменение рубля за 1$ на 4 равных части. Предположим, что компания PepsiCo при курсе 1$ = 35,5 может полностью реализовать произведенную продукцию и получить доход, обозначаемый нами через 1, а при нахождении рубля в промежутке [36,9–45,4), [45,4–53,9), [53,9–62,4) и [62,4–70,9] получить доход соответственно 0,98; 0,95; 0,91 и 0,85 от максимального возможного дохода, равного 1, полученного от полной продажи партии [8].

Из указанных данных видим, что ослабление рубля непропорционально уменьшает доход компании. Это объясняется следующими соображениями. Если рубль по отношению к доллару упал, например, на 3 рубля, то цены на товары будут несколько скорректированы, но это не сильно отразится на спросе, поскольку и корректировка будет несущественной, и люди массово не начнут паниковать из-за такого колебания валют. Если же доллар возрастет на 10 рублей, то это обязательно привлечет пристальное общественное внимание. Цены на продукцию рассматриваемой компании опять же будут скорректированы, однако это изменение может в значительной степени повлиять на спрос, поскольку многие посчитают цену необоснованно завышенной, а некоторые просто не захотят приобретать продукт, который в недавние времена стоил ощутимо дешевле.

Перед руководством компании PepsiCo стоит задача: в указанных выше условиях принять решение о выборе из трех брендов Lay’s, Cheetos, ХрусTeam ? бренда, продуктовая линейка которого будет расширена с целью получения максимальной прибыли от ее реализации.

Для анализа поставленной задачи применим теоретико-игровую модель «Игра с природой» [6].

Во многих задачах принятия финансово-экономических решений важным и неотъемлемым фактором является присутствие неопределённости, заключающейся в недостаточной информированности лица, принимающего решение, об объективных условиях, в которых это решение будет приниматься. Неопределённость такого рода может порождаться различными причинами: нестабильностью экономической ситуации, финансово-экономическим кризисом, покупательским спросом на товар или услуги определённого вида, рыночной конъюнктурой, политикой правительства, надёжностью партнёра по бизнесу, выходом из строя технического оборудования, курсом валюты, уровнем инфляции, налоговой политикой, биржевой ситуацией, экологической обстановкой, стихийными бедствиями и др.

Во всех задачах такого рода выбор решения зависит от объективной действительности, окружающей решаемую задачу и называемой в математической модели «природой». Сама же математическая модель подобных ситуаций называется «игрой с природой» (или статистической игрой).

В игре с природой участвуют два игрока: один из них, обозначим его через A, – лицо, принимающее решение; другой, обозначим его через Π, – природа. Игрок A действует осознанно, стремясь принять наиболее выгодное для себя решение. В отличие от него природа Π принимает то или иное свое состояние неопределенным образом, не противодействуя злонамеренно игроку A, не преследуя конкретной цели и безразлично к результату игры, т.е. природа Π, являясь игроком в игре, не является ни противником, ни союзником игрока A.

Пусть игрок A располагает m возможными стратегиями A1, ..., Am, а природа Π может находиться в одном из n своих состояний Π1, ..., Πn, которые определяются на основании имеющегося опыта анализа состояний природы либо на основании мнений экспертов. Предполагается обычно, что известны результаты выбора игроком A каждой из своих стратегий Ai, i = 1, ..., m, при каждом состоянии природы Πj, j = 1, ..., n, численные значения которых обозначим через aij. Из этих чисел, называемых выигрышами игрока A, формируется матрица его выигрышей размером m×n, строки которой соответствуют стратегиям игрока A, а столбцы – состояниям природы Π.

Таблица 1

Матрица игры с природой размера m×n

Задача игрока A состоит в выборе оптимальной стратегии с использованием по возможности всей информации, содержащейся в матрице A.

Если m = 1, то в распоряжении игрока A всего одна стратегия A1 и проблема выбора оптимальной стратегии отпадает. Поэтому в дальнейшем будем считать m ≥ 2.

Если n = 1, то природа Π пребывает только в одном состоянии Π1. В этом случае проблема выбора игроком A оптимальной стратегии хотя и остается, но превращается в тривиальную: игрок A должен выбрать стратегию, соответствующую строке матрицы A, в которой стоит наибольший из m выигрышей первого (и единственного) столбца матрицы A. Поэтому далее будем предполагать n ≥ 2.

Целесообразно также по возможности упростить матрицу A, уменьшив число ее строк применением принципа доминирования стратегий игрока A [1].

Если вероятности состояний природы неизвестны и нет возможности получить о них какую-либо статистическую информацию, игрок A находится в ситуации принятия решения в условиях неопределенности.

В качестве критерия оптимальности стратегий будем использовать предложенный Л.Г. Лабскером ([5]; см. также [4]) обобщенный выигрыш-критерий Гурвица, который определяется следующим образом. От платежной матрицы переходим к ранжированной матрице B, которая формируется из платежной матрицы путем перестановки элементов каждой строки в неубывающем порядке. Элементы платежной матрицы обозначаются bij. Выигрыши, стоящие в j-м столбце, называются выигрышами j-го ранга. Выигрыши 1-го ранга (стоящие в 1-м столбце ранжированной матрицы) минимальны при каждой стратегии игрока A. Выигрыши j-го ранга (стоящие в последнем столбце ранжированной матрицы) максимальны при каждой стратегии игрока A.

Для учета возможности появления выигрышей вводится вектор неотрицательных коэффициентов 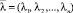, обладающих свойством λ1 + λ2 + ... + λn = 1. Коэффициент λj представляет собой количественную меру уверенности (убежденности) игрока A в том, что при выборе им любой своей стратегии он получит выигрыш j-го ранга. Коэффициенты λ1, λ2, ..., λn выбираются игроком A, вообще говоря, субъективно.

Величина 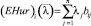, i = 1, ..., m называется показателем эффективности стратегии Ai по обобщенному выигрыш-критерию Гурвицу. Этот показатель учитывает все выигрыши, возможные при каждой стратегии и зависит от значений коэффициентов λ1, λ2, ..., λn, которые выступают в качестве весов вклада каждой стратегии в показатель эффективности.

Оптимальной во множестве чистых стратегий называется стратегия с максимальным показателем эффективности ([4, 5]).

Числа

Очевидно, что λp + λo = 1.

При выборе коэффициентов следующим образом: λ1 ≥ 0, λ2 = ...= λn–1, λn = 1– λ1, ? обобщенный выигрыш-критерий Гурвица превращается в классический выигрыш-критерий Гурвица ([9, 6]), который наиболее часто применяется для оптимизации коммерческой деятельности на практике. Он является промежуточным критерием между максимаксным критерием – критерием крайнего оптимизма и критерием Вальда – критерием крайнего пессимизма.

Отметим, что классический выигрыш-критерий Гурвица не учитывает всех выигрышей при каждой стратегии и принятие решения базируется на основании только наименьшего и наибольшего выигрыша. Обобщенный выигрыш-критерий Гурвица позволяет учесть весь спектр возможных выигрышей [6].

Известны ([3, 2]) формализованные методы выбора коэффициентов обобщенного выигрыш-критерия Гурвица, призванные ограничить субъективный произвол выбора этих коэффициентов игроком A. Используем один из них, в основу которого положено то, что в ранжированной матрице B все элементы по строкам упорядочены в порядке неубывания.

Введем следующие обозначения:

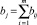– сумма выигрышей по j-му столбцу матрицы B;

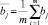– среднее значение выигрыша по j-му столбцу матрицы B;

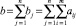– сумма всех выигрышей матрицы B.

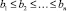и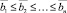

Игроку A предлагаются два подхода к выбору оптимальной стратегии [3]:

? более осторожный, при котором коэффициенты λj убывают с ростом средних значений выигрышей по столбцам;

? более оптимистичный, при котором значения коэффициентов λj возрастают с ростом средних значений выигрышей по столбцам.

Выбор подхода (оценка реальной ситуации на предмет опасности) возлагается на игрока A. При безопасной ситуации (оптимистичном подходе) 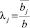. При опасной ситуации (пессимистичном подходе) 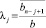[6, § 4.11, с. 565].

Проведем математическую формализацию задачи.

Пусть в модели «Игра с природой» сознательный игрок A – это руководство компании PepsiCo, которое в своем распоряжении имеет три чистых стратегии – инвестировать в новый бренд: A1 – в Lay’s, A2 – в Cheetos, A3 – в ХрусTeam.

Пусть роль «Природы» играет курс валюты в указанный период с 31.08.2014 по 31.08.2015. Природа может пребывать в одном из своих четырех состояний: рубль находится в промежутке: Π1 – [44,96; 50,04); Π2 – [50,04; 55,84); Π3 – [55,84; 61,28); Π4 – [61,28; 66,72] [8]. В качестве выигрышей игрока A будем рассматривать прибыли от инвестирования в новый продукт бренда в полном объеме, представляющие собой разность между доходом от выпуска продукта и издержками на его производство.

Результаты расчета дохода и издержек представлены в следующих соответствующих таблицах.

Таблица 2

Матрица выручки

После вычитания затрат из выручки получаем матрицу выигрышей.

Таблица 3

Матрица выигрышей

Матрицу выигрышей можно упростить, преобразуя ее дробные элементы в целые числа. Для этого подвергнем ее аффинному преобразованию 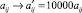, i = 1, 2, 3; j = 1, 2, 3, 4.

Таблица 4

Матрица выигрышей после аффинного преобразования

В соответствии с определением обобщенного выигрыш-критерия Гурвица составим ранжированную матрицу B. На основании данной матрицы рассчитаем показатели эффективности стратегий и найдем оптимальные стратегии.

Таблица 5

Матрица решения задачи

Выигрыши 1-го ранга наименьшие и представляют собой показатели эффективности стратегий по критерию Вальда. Выигрыши 4-го ранга наибольшие и являются показателями эффективности стратегий по максимаксному критерию.

Сумма всех выигрышей 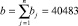. Следовательно, коэффициенты λ1, λ2, λ3, λ4 можно выбрать обратно пропорциональными неубывающей последовательности средних выигрышей:

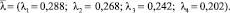
Показатель эффективности первой стратегии рассчитывается по формуле

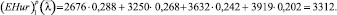
Показатели эффективности двух других стратегий рассчитываются аналогично. Оптимальной стратегией является вторая стратегия игрока A.

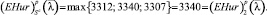
Таким образом, опираясь на обобщенный критерий Гурвица, компании PepsiCo следует приниматься за реализацию второго инвестиционного проекта, т.е. инвестировать в бренд Cheetos.

Библиографическая ссылка