Динамика играет важную роль в управлении роботами. Существуют два типа динамических моделей [5]:
– обратная задача динамики: по заданным траектории движения, скоростям и ускорениям X, W,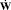 
рабочего органа определить силы в приводных кинематических парах τ. В общем виде обратная задача динамики формулируется как
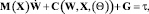
где M – положительно определенная матрица инерции; G – гравитационная составляющая; C – центробежная и кориолисова составляющая. Эта формула полностью аналогична формуле для последовательных роботов;
– прямая задача динамики: по заданным силам/моментам в приводных кинематических парах определить траекторию, скорости и ускорения рабочего органа.
Рассмотрим параллельный робот, основание и подвижная платформа которого соединены посредством 6 опор, присоединенных к основанию посредством универсальных шарниров, а к подвижной платформе – посредством сферических шарниров (рис. 1). Опоры приводятся в движение посредством призматических шарниров.
Для получения обратной динамической модели такого робота разобьем его на две подсистемы: подвижную платформу и опоры.
Динамика подвижной платформы определяется как функция ее декартовых координат (положения, скоростей и ускорений), а динамика опор определяется как функции их обобщенных координат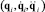 
. Усилия в приводных кинематических парах могут быть получены посредством проецирования этой динамической модели на оси приводных кинематических пар.
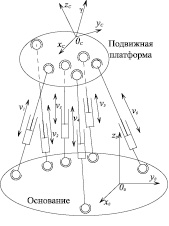
Рис. 1. Схема параллельного робота
Для проецирования динамических характеристик платформы в пространство приводных кинематических пар умножим их на транспонированный якобиан механизма, а для проецирования динамических характеристик опор в пространство приводных кинематических пар используем якобиан, выражающий связь между этими пространствами. Тогда динамическая модель механизма параллельной структуры будет описываться следующим уравнением:
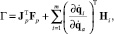(1)
где Fp – вектор обобщенных сил и моментов, приложенных к платформе; Jp – якобиан механизма размерностью 6×n, выражающий зависимость поступательных и угловых скоростей платформы от скоростей движения приводных кинематических пар,
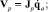(2)
Hi – обратная динамическая модель опоры i, представленная в виде функции от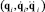 
. Она может быть получена в терминах положений, скоростей и ускорений платформы из обратной кинематической модели опор.
Если число степеней свободы механизма меньше 6, вектор Vp может быть редуцирован до вектора Vr, соответствующего n независимых степеней свободы механизма. Тогда Vp может быть выражен через Vr как
Vp = SVr, (3)
где
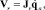(4)
и выражение (3) может быть переписано в виде
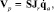(5)
где Jr – редуцированный кинематический якобиан механизма размерностью n×n. Заметим, что при n = 6 матрица S представляет собой единичную матрицу размерностью 6×6. Для вычисления Jr следует инвертировать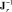 
.
В общем случае, когда платформа имеет 6 6 степеней свободы, Fp вычисляется посредством уравнения Ньютона ? Эйлера [2]:
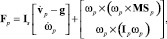(6)
где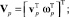 
vp – линейные скорости центра системы координат XYZp, связанной с платформой; ωp – угловые скорости системы координат XYZp; 
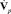– ускорение платформы, получаемое путем дифференцирования (5)
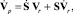(7)
где g – ускорение свободного падения, разложенное по осям системы координат XYZp; Ip – матрица инерции платформы относительно центра системы координат XYZp; MSp – вектор начальных моментов платформы относительно системы координат XYZp:
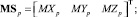(8)
Is – пространственная матрица инерции платформы:
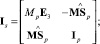(9)
Mp – масса платформы; E3 – единичная матрица размерностью 3×3;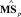 
– кососимметричная матрица размерностью 3×3, соответствующая вектору MSp
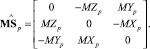(10)
Вычисление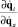 
можно произвести по следующей формуле, вытекающей из параллельной структуры механизма:
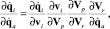(11)
где vi – вектор линейных скоростей, сообщаемых i-й опорой платформе.
Выражение (11) можно переписать как
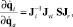(12)
где Ji – кинематический якобиан опоры i, соответствующий выражению
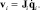(13)
Методы вычисления Ji широко известны [2], Jvi определяет соотношение между vi и Vp,
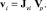(14)
В конечном итоге из (1) и (11) получаем следующую компактную форму обратной модели динамики механизма параллельной структуры:
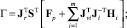
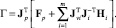(15)
Для вычисления Hi можно использовать множество методов. Для уменьшения вычислительной сложности задачи целесообразным видится применение рекурсивного алгоритма Ньютона ? Эйлера [4].
С учетом (12) и того, что активные переменные независимы, выражение обратной модели динамики может быть записано в виде
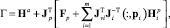(16)
где Ha – вектор приводных сил/моментов всех опор, соответствующий компонентам Hi, описывающим приводные шарниры (i = 1, ..., m); pi – номера столбцов, соответствующих силам/моментам пассивных шарниров опоры i;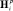 
– вектор сил/моментов в пассивных шарнирах опоры i.
Теперь уравнение (16) может быть переписано в следующей форме:
Такая форма существенно упрощает модель, позволяя избежать излишних умножений активных сил/моментов на проективную матрицу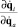 
. Кроме того, возникает преимущество в возможности расчета кинематики и динамики опор параллельно на m процессорах.
Расчет обратной динамической модели требует вычисления обратного якобиана опор и кинематического якобиана механизма.
В связи с этим разработан новый метод расчета обратного кинематического якобиана механизма с использованием обратных якобианов его опор.
Кинематический якобиан механизма представляет собой соотношение между скоростями приводных кинематических пар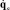 
и пространственными скоростями платформы Vr
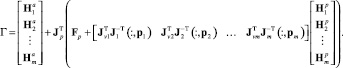(17)
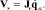(18)
В общем случае Jr вычисляется путем инвертирования матрицы обратного якобиана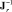 
, так как ее проще вычислить.
Для вычисления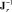 
очевидным решением является использование соотношений между скоростями в кинематических парах и скоростями платформы через опору i с учетом перехода от неподвижной системы координат, связанной с основанием, к подвижной системе координат, связанной с платформой [3]:
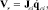(19)
где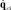 
– вектор скоростей всех (включая пассивные) кинематических пар опоры i, от платформы к звену, соединенному с основанием; Jci – кинематический якобиан последовательного перехода от неподвижной системы координат, связанной с основанием, к системе координат, связанной с подвижной платформой, через опору i.
Решим (18) относительно скорости приводной кинематической пары опоры i:
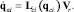(20)
Тогда обратный кинематический якобиан механизма может быть получен путем группировки Lci для всех опор:
(21)
В соотношении (18) используются данные о пассивных кинематических парах опоры i. С целью упрощения расчетов эти переменные можно исключить, воспользовавшись соотношением между выражениями для скорости в точке соединения опоры с подвижной платформой vi, выраженной, с одной стороны, в терминах Vr
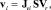(22)
и, с другой стороны, в терминах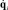 
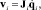(23)
где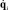 
– вектор скоростей в кинематических парах опоры i без учета пассивной кинематической пары, соединяющей опору с основанием; Ji – кинематический якобиан опоры i от неподвижного основания к точке соединения с платформой; Jvi – якобиан, преобразующий скорость платформы в скорость в точке соединения ее опорой i, связанный исключительно с этой опорой.
Решение уравнения (23) для активной кинематической пары опоры i дает:
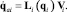(24)
Затем, с помощью (22) и перегруппировки для всех опор, получаем
(25)
и, следовательно,
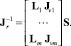(26)
Для робота с шестью степенями подвижности (рис. 1) проведен расчет динамических характеристик [1], исходными данными для которого являются ускорения рабочего органа: γx = 1 см/с2, t ∈ [0, 2]; γx = –1 см/с2, t ∈ [2, 4]; γy = 5 см/с2, t ∈ [0, 4] другие компоненты вектора ускорений равны нулю.
Начальные линейные и угловые скорости рабочего органа равны нулю, начальное положение [0; 0; 53,3], начальная ориентация [0; 0; 0]. Координаты, x, y рабочего органа представлены на рис. 2, усилия в шарнирах – на рис 3.
Рис. 2. Координаты x, y рабочего органа, полученные для заданных ускорений
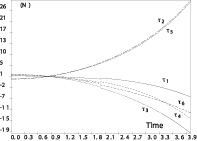
Рис. 3. Усилия в шарнирах при траектории, рассчитанной с применением обратной модели динамики
Предположим, что рабочий орган осуществляет вертикальное перемещение из начального положения. Обратная задача динамики показывает, что в этом случае все линейные приводы должны развивать одинаковое усилие, равное 1,65 65 Н. Однако ошибка в модели одного из приводов приводит к реальным усилиям
τ1 = 1,6665 Н; τi = 1,65 H;
∀i ∈ [2, 6].
Начальные линейные и угловые скорости примем равными нулю, начальное положение рабочего органа (0; 0; 53,3), все углы Эйлера равны нулю.
Работа выполнена при финансовой поддержке РФФИ, грант № № 14-01-00761.
Библиографическая ссылка
Рыбак Л.А., Гапоненко Е.В., Чичварин А.В. ПОСТРОЕНИЕ ОБРАТНОЙ ДИНАМИЧЕСКОЙ МОДЕЛИ ПАРАЛЛЕЛЬНЫХ РОБОТОВ МЕТОДАМИ СТРУКТУРНОЙ ДЕКОМПОЗИЦИИ // Фундаментальные исследования. 2015. № 11-7. С. 1358-1362;URL: https://fundamental-research.ru/ru/article/view?id=39838 (дата обращения: 02.04.2025).