Повысить производительность лесотранспортных машин можно методом активного увеличения проходимости за счет управления несущей способностью путей первичного транспорта леса. В свою очередь, ресурсы для увеличения несущей возможности путей ограничиваются способностями древостоя, биопродуктивность которого определяется режимом увлажнения и рельефом местности, другими словами, категорией местности. Проходимость рассматриваем как способность лесозаготовительной машины совершать технологическую работу без нарушения (в допустимых границах) плодородия лесной земли и возможностью преодоления разных препятствий (пней, валунов, валежника) [2, 3, 7, 8]. В работах ученых [1–3, 5–6], приведены зависимости проходимости гусеничных и колесных машин в меняющихся грунтовых критериях. Тут проходимость машин первичного транспорта леса определяется коэффициентами: сопротивления качению, сопротивления от наклона, сцепления и буксования, также удельным давлением на грунт и несущей способностью грунта. В главном исследователи уделяли внимание технической проходимости, т.е. возможности лесозаготовительных и лесотранспортных машин передвигаться по лесосеке с определенной силой тяги [4, 5]. Но эти зависимости не позволяют оценить воздействие на производительность лесных машин. Проходимость комплексных трелевочно-транспортных систем (КТТС) ограничивается [1, 2, 3, 4]:
– особенностями конструкции ходовой части, величиной массы и ее распределением на опорные части;
– путевыми условиями или, при работе без дорог, особенностями местности и другими природными факторами, в первую очередь:
1) почвенно-грунтовыми условиями;
2) рельефом местности;
3) наличием естественных непреодолимых препятствий.
С учетом этого при оценке проходимости машины следует рассматривать систему: машина – естественная (грунтовая) ездовая поверхность.
Взаимодействие этой системы описывается уравнением
Fизб = Fсц – Wпол, (1)
где Fизб – избыточная (свободная) сила тяги, которая может быть использована на преодоление уклонов и перевозку сортиментов, Н; Fсц – максимальная сила тяги (по сцеплению), Н; Wпол – сопротивление движению машины (Н/т), величину которого можно принять равной
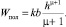(2)
Величина h, в свою очередь,
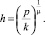(3)
Таким образом,
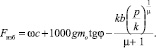(4)
Разделив Fизб на ω, получим
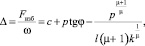(5)
где l – суммарная длина отпечатков колес КТТС, м.
В формуле (5) величина Δ зависит от удельного давления колеса – р (Н/см2).
Отношение Δp в известной мере характеризует конструкцию машин и ее пригодность для данной ездовой поверхности.
Оптимальное значение Δ:р может быть получено дифференцированием выражения (5).
Однако в правой части (5) имеется величина l, зависящая от р. Ее можно найти из равенства
ω = nεl2,
где ε – отношение средней ширины следа к его длине; n – количество колес у КТТС.
В то же время
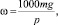(6)
где m – масса КТТС, т.
С учетом этого
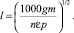
Таким образом,
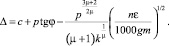(7)
Дифференцируя, будем иметь
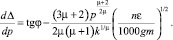
Приравняв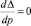 
, получим
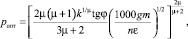(8)
где c – сцепление, Н/см2; k – коэффициент, характеризующий физико-механические свойства грунта; μ – коэффициент, характеризующий состояние грунта; φ – угол внутреннего трения грунта (коэффициент пропорциональности между максимальными касательными и нормальными напряжениями при разрушении грунта).
Приняв n = 4 м и μ = 0,5, будем иметь
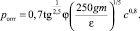(9)
Например, при tgφ = 0,36, m = 8 т; k = 7; ε = 1
pопт = 0,7?0,87?7,34?4,7 = 16 Н/см2.
Зная оптимальное значение удельного давления на ездовую поверхность, можно определить основные параметры КТТС, при которых можно получать наибольшую величину удельной свободной силы тяги на каждый квадратный сантиметр опорной поверхности [5].
При с = 1,5 Н/см2 будем иметь по формуле (7), что
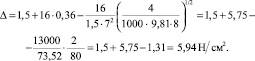
Величина опорной поверхности (суммарной площади всех отпечатков колес) равна
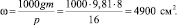
а свободная сила тяги по сцеплению
Fизб = 4900?5,94 = 29100 Н.
Соответственно, касательная сила тяги у такой машины должна быть равна
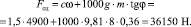
Сопротивление КТТС самопередвижению определится
Wкол = 36150 – 29100 = 7050 Н,
а удельное сопротивление движению
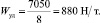
Коэффициент сцепления
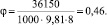
Изложенная ниже методика позволяет подойти и к определению неизвестного показателя pD для КТТС. Диаметр эквивалентного круга
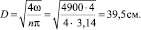
Таким образом, оптимальное значение
pD = 16?39,5 Н/см.
Задаваясь предельной величиной вертикальной деформации колеса, можно определить диаметр колеса КТТС. Пользуясь известной формулой Хедекеля, можно написать
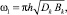(10)
где ω1 – площадь следа одного колеса, см2; h – вертикальная деформация шины колеса, см; Dk – диаметр колеса, см; Bk – ширина беговой дорожки (0,85…0,9 ширины профиля шин), см.
В то же время
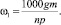(11)
У трелевочных тракторов величина h, зависящая от Dk, колеблется в узких пределах и может быть принята равной h = aDk, где a = 0,04…0,048.
Имея это в виду и приравняв друг другу правые части равенств (10) и (11), можно получить, что
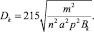(12)
При m = 8 т; n = 4; a = 0,042; р = 16 Н/см2 и Bk = 45 см получим
Полученные зависимости характеризуют влияние физико-механических свойств грунта и его состояния (влажности) на величину сцепления ведущих колес машин с ездовой поверхностью и позволяют установить оптимальные значения среднего удельного давления колеса трелевочно-транспортной системы, диаметра колеса и, следовательно, величины pD, характеризующей воздействие системы на ездовую поверхность, а также минимальный радиус проходимости и другие характеристики.
Таким образом, получены расчетные формулы, которые позволяют установить оптимальное значение величины удельного давления колесных машин на ездовую поверхность и диаметра колеса.
Библиографическая ссылка
Бурмистров Д.В., Арутюнян А.Ю., Бурмистрова О.Н. ПРОХОДИМОСТЬ КОМПЛЕКСНЫХ ТРЕЛЕВОЧНО-ТРАНСПОРТНЫХ СИСТЕМ НА ТРЕЛЕВОЧНЫХ ВОЛОКАХ // Фундаментальные исследования. 2015. № 11-7. С. 1304-1307;URL: https://fundamental-research.ru/ru/article/view?id=39828 (дата обращения: 02.04.2025).