Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Севодин М.А. 1 Петров А.Д. 1

---

1 ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет»

Настоящая работа посвящена изучению возможностей использования оптимизационных схем теории портфеля ценных бумаг. Неопределенность будущих последствий финансовых решений, которые могут повлечь финансовые потери (или принести недостаточно высокие доходы) по сравнению с прогнозируемым вариантом, обусловливает необходимость серьезного обоснования таких решений с помощью технологий, испытанных в условиях развитых финансовых рынков. В статье принципы построения оптимального портфеля, базирующиеся на индексной EGP-модели, адаптируются к управлению деятельностью «многопродуктового» предприятия. Для этого используются не только доходности и их колебания товаров, но и издержки производства. Во второй части работы рассматриваются принципы деятельности торгового предприятия. Формируются группы товаров по приоритетности, строится модель для оптимизации товарного запаса предприятия. Дана практическая иллюстрация этой модели.

Статья в формате PDF

573 KB

доходность

риск

издержки

торговое предприятие

оптимизация

1. Казаков В.А., Тарасов A.B., Зубицкий А.Б. Модели формирования портфеля акций в современной теории инвестиций // В.А. Казаков, A.B. Тарасов, А.Б. Зубицкий // Финансы и кредит. – 2006. – № 5. – С. 17–21.

2. Карпиков Е.И., Федоров А. Основные постулаты классической теории портфельных инвестиций [Электронный ресурс]. – Режим доступа: http://www.masters.donntu.edu.ua/2007/iVti/toichkina/library/invest3.htm

3. Касимов Ю.Ф. Основы теории оптимального портфеля ценных бумаг. – М.: Филинъ, 1998. – 142 с.

4. Лукашин Ю.П. – Оптимизация структуры портфеля ценных бумаг // Экономика и математические методы. – 1995. – Т. 31. – Вып. 1. –С. 138–150.

5. Меньшиков И.С. – Финансовый анализ ценных бумаг. – М.: Финансы и статистика, 1998. – 360 с.

6. Шведов А.С. Теория эффективных портфелей ценных бумаг. – М.: ГУ ВШЭ, 1999. – 191 с.

Одной из ключевых задач деятельности торгового предприятия является увеличение продаж за счет оптимизации сбыта. Особый интерес здесь представляет управление процессами оптимизации ассортимента продаваемых товаров или услуг. Здесь важной проблемой для современных торговых предприятий розничной торговли следует считать оптимизацию товарных остатков. Ввиду того, что на таких предприятиях (магазинах) очень широкий ассортимент продукции, где каждая позиция имеет свои индивидуальные характеристики, довольно сложно систематизировать и оптимизировать товарный запас. Также существует множество различных ограничений, описанных условиями хранения, способами доставки и т.д. Несмотря на это каждому виду товаров можно присвоить свои определенные уровни доходности и издержек. Этот момент является принципиальным при изучении названной проблемы.

Основная цель работы – найти метод для оптимизации товарного остатка, используя разумную комбинацию долей представляемого ассортимента. В первой части работы моделируется деятельность «многопродуктового» предприятия. В основу выбора структуры производимой продукции предлагается взять EGP-модель из теории оптимального портфеля ценных бумаг [1–3], смысл которой заключается в нахождении максимального значения соотношения доходности к риску при выборе состава выпускаемых товаров. Отметим, что без проведения процедуры оптимизации невозможно провести анализ наиболее выгодных ассортиментных единиц, дающих предприятию наибольшую доходность при минимальном риске [4]. Предлагаемая модель привлекательна еще и тем, что позволяет использовать гибкую систему ограничений, которые можно дополнять в процессе её решения, сюда можно включить всевозможные условия, принципы, по которым работает предприятие. В заключении статьи рассматривается конкретный пример применения предложенной методики.

Модель оптимизации деятельности предприятия

Рассмотрим деятельность предприятия, связанную с производством товаров. Вектор X = (x1, ..., xn) соответствует набору товара i в количестве xi. Будем считать, что само предприятие не влияет на цены, уверено в возможности реализации всей продукции и стремится оптимизировать свою деятельность за счет выбора структуры выпускаемой продукции. Под такой структурой понимается соотношение долей товаров в общем объеме выпуска.

Доходность товара определяется на основе стоимости его покупки и последующей продажи. Так как на стоимость покупки товара влияет множество рыночных факторов, управление портфелем товаров протекает в условиях неопределенности, которая порождает риск неэффективного управления. В данной работе предполагается, что стоимость товара не остается постоянной, а изменяется в определенном интервале.

Определим доходность товара Sit товара xi, i = 1, ..., n в момент времени t, t = 1, ..., T, T – объем выборки (число наблюдений), по формуле

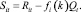
Здесь 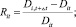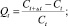Dit – цена единицы i-го товара в момент времени t, fi(k) – коэффициент, характеризующий долю издержек производства, затраченных на единицу i-го товара. Будем считать, что fi(k) зависит от вектора k = (k1, ..., kn), а Rit и Qt – независимые случайные величины.

Очевидно, что 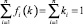. Отсюда следует, что в момент времени t доходность равна

.

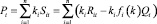Математическое ожидание доходности производства также является взвешенной средней ожидаемых доходностей отдельных товаров:

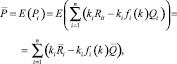
где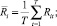

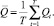
Для рассматриваемого производства риск можно оценить стандартным отклонением :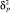

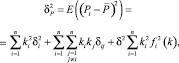
причем

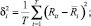
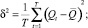
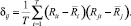
Из полученных формул следует, что имеется возможность использовать для оптимизации деятельности предприятия методы теории портфеля ценных бумаг (см., напр., [5–6]). В частности, ясно, что наилучшее соотношение между приростом доходности и возрастанием риска можно найти с помощью максимизации функции [4].

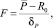
где R0 соответствует тем 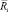, для которых δi = 0.

Задача оптимизации этой функции с учетом равенства 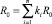сводится к определению коэффициентов ki, максимизирующих функцию

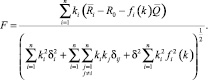
Предположим, что функции fi(k), i = 1, ..., n, дифференцируемы. Найдем частные производные функции F по искомым параметрам, а затем приравняем их нулю. Получим систему n уравнений

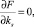s = 1, ..., n; (1)

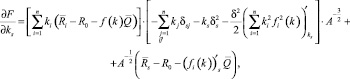
где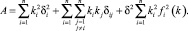

Если потребовать от функций fi(k) специального вида, то можно исследовать полученную систему (1) и найти оптимальное решение k = (k1, ..., kn). В частности, если положить 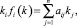i = 1, ..., n то k = (k1, ..., kn) находится с помощью линейной системы

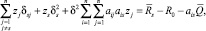
s = 1, ..., n,

где zs и ks связаны соотношением

zs = λks;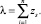

Практическая реализация

Покажем на конкретном примере, как можно использовать описанную выше модель для оптимизации товарного запаса на торговом предприятии. Суть задачи заключается в следующем: нужно определить оптимальное соотношение между видами товаров для получения наибольшей прибыли, исходя из данных о продажах за предыдущий период. Полученные результаты дадут ясную картину для понимания, какой товарный запас нам потребуется в дальнейшей деятельности. Весь товар в магазине имеет структурированную иерархию. Сначала он разделяется по субкатегориям, здесь товар классифицируется по видам, форме, составу. Следующая иерархическая ступень – это категории, объединяющие в себе несколько субкатегорий. Каждая категория объединяет общие свойства продукта по предназначению. Последней иерархической ступенью служат «направления», в нее входят всего три классификации: «Продовольственное», «Непродовольственное», «Алкоголь». Обычно так делается для упрощения работы с отдельными видами товара и анализа по каждой классификации.

Таблица 1

Исходные данные (шт.), Я* – Ярлыки

Существует метод АВС – каждой субкатегории присваивается ярлык со значением А, В или С, который показывает степень рентабельности товара. Так, к ярлыку А относят наиболее востребованные и прибыльные виды товаров, к ярлыку В не менее важные, чем А, но большие по себестоимости (то есть имеющие повышенные издержки, особые условия хранения), в категории С входят субкатегории, не обладающие особым спросом.

Обычно, исходя из стратегии предприятия, вводят некоторые ограничения на ярлыки АВС. Стандартными ограничениями являются следующие: субкатегории с ярлыком А должны занимать не менее 40 % в общем товарном запасе; товары с ярлыком В не более 40 % товарного запаса, все остальное приходится на товары с ярлыком С (АВС – 40/40/20). Названные ограничения будем учитывать при определении пропорций между товарами.

Возьмем данные о продажах по субкатегориям в одном из магазинов г. Перми (магазин «Дельта»). Период продаж – май 2013 года. Для упрощения рассмотрим лишь одну категорию – «Бакалея» с периодом одна неделя. Пример таких данных приведен в табл. 1 (продажи по субкатегориям в единицах на каждый день недели).

Теперь, с учетом цен, можно воспользоваться предложенной методикой (издержки берутся равными нулю) и найти оптимальные значения ki. Эти значения приведены в табл. 2.

Таблица 2

Оптимальные значения ki

В столбце «Фактические доли» (табл. 2) стоят значения фактического распределения субкатегорий в долевом соотношении. Проанализировав фактическое распределение и полученные в результате решения данные, видим, что следует провести перераспределение товарного объема по различным субкатегориям: стоит увеличить позиции 8, 16, 19 за счет уменьшения позиций 10, 11, 21.

Итак, главным результатом проведенного исследования является оптимизационная модель деятельности предприятия. Приведенный пример показал реализуемость построенной модели. Кроме того, видно, что предлагаемую методику несложно модифицировать и для случая большего числа ограничений, и для случая больших промежутков времени.

Библиографическая ссылка