В России уже достаточно давно освоен выпуск авиационных газотурбинных установок (ГТУ) для нужд электроэнергетики [9, 8]. Как известно, ГТУ является работоспособной только при наличии системы автоматического управления (САУ), поэтому задачам совершенствования САУ ГТУ для авиации уделяется самое серьезное внимание [4]. При управлении наземными электроэнергетическими ГТУ возникают специфические проблемы, связанные с особенностями функционирования синхронного генератора как объекта управления и с необходимостью обеспечения требуемых параметров электропотребления [8]. Поэтому оправдан поиск перспективных алгоритмов управления ГТУ для обеспечения качества вырабатываемой электроэнергии во всех эксплуатационных режимах и с учетом нелинейных свойств объекта управления – синхронного генератора. Более того, апробацию перспективных САУ для наземных ГТУ можно одновременно рассматривать как площадку для отработки перспективных решений для авиации. Среди перспективных САУ в первую очередь обращает на себя внимание возможность использования механизмов адаптации, то есть построение САУ ГТУ в классе адаптивных систем [3, 10]. В первую очередь рассматривались адаптивные системы управления с эталонной моделью, построенные по рекомендациям из [3, 10]. В работах [1, 5] мы рассмотрели схему с эталонной моделью и сигнальной настройкой. В этой статье рассматривается схема с эталонной моделью и параметрической настройкой.
В работе [3] рекомендовано использовать параметрическую настройку при существенном преобладании нестационарных свойств; сигнальную настройку при преобладании нелинейных свойств, и совместно оба типа настройки при обоюдном проявлении нелинейных и нестационарных свойств (рис. 1).
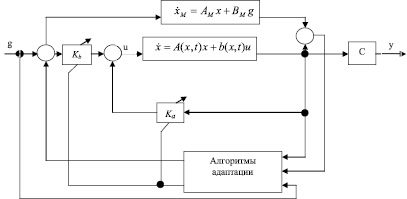
Рис. 1. Структурная схема системы с параметрической и сигнальной настройкой
В связи с этим исследование параметрической настройки в дальнейшем проводится для модели ГТУ, в которой явно проявляются нестационарные свойства.
В качестве метода адаптации, как и в статье [5], целесообразно выбрать метод функций Ляпунова из соображений сокращения времени поиска экстремума [3].
В работе [5] предложен следующий алгоритм для параметрической адаптации:
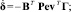
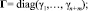γi > 0, (1)
где 
– это вектор добавочных коэффициентов, которые корректируют параметры регуляторов САУ; v – расширенный вектор состояния нестационарной системы; В – матрица управления эталонной модели; матрица Р является решением матричного уравнения 
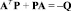, где матрицу Q рекомендуется выбирать диагональной положительно определенной; е – вектор ошибки между эталонной моделью и испытуемой нестационарной системой; Г – диагональная положительно определенная матрица, которая выбирается согласно рекомендациям [3].
Линейная нестационарная модель ГТУ для исследования адаптивных регуляторов
Для исследования параметрической настройки построим модель ГТУ. Для этого используем упрощенную динамическую модель ГТУ, полученную с помощью идентификации методом наименьших квадратов [6]. Модель сохраняет допустимую адекватность для работы САУ ГТУ в режиме стабилизации частоты вращения свободной турбины ГТУ от холостого хода до 1,2 номинальной нагрузки.
Линейная модель состоит из двух уравнений:
а) уравнение ротора турбокомпрессора:
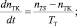(2)
б) уравнение свободной турбины:
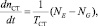(3)
где обозначено TСТ = nСТJ – постоянная времени свободной турбины;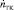 
– производная приведенной частоты вращения ротора турбокомпрессора по времени; nТК – приведенная частота вращения ротора турбокомпрессора; nСТ – частота вращения ротора свободной турбины; nTS – частота вращения ротора турбокомпрессора, взятая по статической характеристике; J – суммарный приведенный к валу момент инерции свободной турбины; TT – постоянная времени ротора турбокомпрессора; NE – располагаемая мощность свободной турбины; NG – потребляемая мощность нагрузки (синхронного генератора).
Таким образом, передаточную функцию линейной модели можно представить в виде
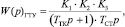(4)
где K1 – коэффициент усиления постоянного времени турбокомпрессора, K2 – коэффициент преобразования nТК в NE; K3 – коэффициенты усиления постоянного времени свободной турбины.
Для получения нестационарной модели в ее состав включены нестационарные блоки: НcБ1, НcБ2.
На рис. 2 изображена структурная схема полученной модели ГТУ [6, 7]. Здесь обозначено: GТ – расход топливного газа.
На рис. 3 показана нестационарная линейная модель ГТУ в составе САУ с двумя регуляторами, включенными по схеме подчиненного регулирования [2]. Внутренний регулятор пропорционально-интегральный, внешний – пропорциональный.
Передаточная функция ПИ – регулятора турбокомпрессора имеет вид
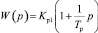, (5)
где Kp1 – коэффициент усиления ПИ регулятора; Tp – постоянная времени ПИ-регулятора. На этом же рисунке обозначен Kp2 – коэффициент усиления П-регулятора свободной турбины.
Параметрическая настройка по трем переменным
Рассмотрим работоспособность алгоритма (1) параметрической настройки на численном примере. Заданы следующие значения параметров модели (2)–(4):
K1 = 44,72; K2 = 1; K3 = 0,26315;
ТТК = 0,5; ТТК = 0,5; Kp1 = 0,074;
Kp2 = 2,5; Тр = 0,5.
Нестационарные блоки заданы следующим образом:
НсБ1 – k1(t) = 0,5t + 44,72;
HсБ2 – k2(t) = 0,5t + 1.
Эталонная модель представлена в пространстве состояний.
Для этого вначале следует преобразовать структурную схему на рис. 3 выделив явно все единичные интеграторы (рис. 4).
Уравнения пространства состояний:
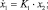
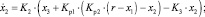
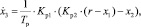(6)
где x1 – частота вращения свободной турбины; x2 – частота вращения турбокомпрессора; x3 – выход интегратора ПИ-регулятора. Тогда матрица коэффициентов эталонной модели примет вид
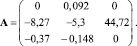(7)
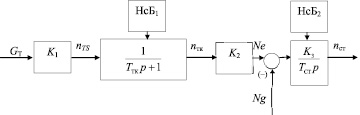
Рис. 2. Линейная нестационарная модель ГТУ
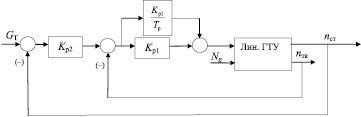
Рис. 3. Нестационарная линейная модель ГТУ в составе САУ
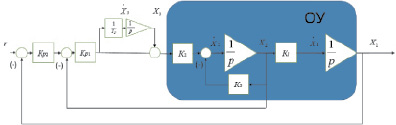
Рис. 4. Преобразованная структурная схема
Матрица управления ЭМ:
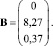(8)
В зависимости от выбора матрицы Q матрица P и результат параметрчиеской настройки будет различным. По результатам экспериментов была выбрана следующая матрица Q = diag (–10 –10 –10).
В результате расчета по уравнению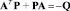 
матрица P имеет следующий вид:
(9)
Алгоритм параметрической адаптации получаем в следующем виде
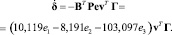(10)
Вектор производных добавок 
является трехмерным. Из них δ1 добавляется к KР2, δ2 добавляется к KР1, δ3 добавляется к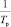 
.
Возмущение Ng подавалось на 5 секунде (сброс от 2000 до 1000 кВт) и на 9,5 секунде (наброс с 1000 до 2500 кВт). На рис. 5 показаны результаты моделирования. Здесь обозначено: 1 – эталонная модель; 2 – линейная нестационарная модель с параметрической настройкой; 3 – линейная нестационарная модель без параметрической настройки.
Как мы видим по графику, линейная нестационарная модель (3) без параметрической настройки ведет себя существенно хуже эталонной модели (стационарной). Исключим ее из сравнительного анализа для подробного ознакомления с временными характеристиками систем с эталонной моделью (1) и с линейной моделью с параметрической настройкой (3) для первого участка, показанного на рис. 5 (взят отрезок в пределах от 0,3 до 0,5 с). В результате получаем, что модель параметрической настройкой выполняет колебания вокруг траектории эталонной модели, с течением времени амплитуда колебаний уменьшается (рис. 6).
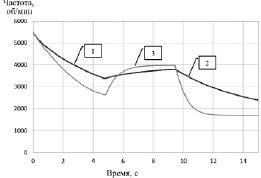
Рис. 5. Временные характеристики (частота вращения свободной турбины nСТ ГТУ)
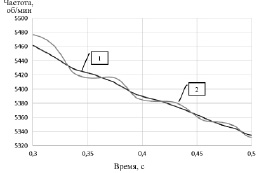
Рис. 6. Временные характеристики (частота вращения свободной турбины nСТ ГТУ)
Вывод
Методика адаптивного управления с эталонной моделью и параметрической настройкой может быть работоспособна при управлении нестационарными ГТУ. Однако необходимо учитывать диапазон изменения параметров, что существенно влияет на результаты адаптации. Кроме того, следует учитывать физические ограничения, среди которых одним из ведущих является ограничение по расходу топлива GT. Проверка с нелинейной моделью подтвердила вывод из работ [3, 10], что параметрическая настройка работоспособна для нестационарной модели, а для нелинейной модели качество работы резко ухудшается. Полученные результаты требуют проведения на полученной основе дальнейших исследований.
Библиографическая ссылка
Зиятдинов И.Р., Кавалеров Б.В. ИССЛЕДОВАНИЕ СИСТЕМЫ УПРАВЛЕНИЯ С ЭТАЛОННОЙ МОДЕЛЬЮ И ПАРАМЕТРИЧЕСКОЙ НАСТРОЙКОЙ ДЛЯ ЭЛЕКТРОЭНЕРГЕТИЧЕСКОЙ ГАЗОТУРБИННОЙ УСТАНОВКИ // Фундаментальные исследования. – 2015. – № 12-6. – С. 1107-1111;URL: https://fundamental-research.ru/ru/article/view?id=39738 (дата обращения: 14.10.2024).