Динамическое исследование развития современной экономики с учетом происходящих изменений свидетельствует о том, что за довольно продолжительный период потенциалы экономики различных стран, как правило, растут. При этом наблюдается такая форма развития, как «бычий тренд», на который оказывают влияние колебания экономического роста, называемые экономическими циклами. Степень влияния зависит как от объективных причин, так и от возможных ошибок в планировании [2, 4].
Одним из методов анализа причин изменения экономики с использованием различных сценариев является математическое моделирование протекающих процессов [3, 6].
Среди математических моделей оценки экономического роста наиболее приемлемой является модель Харрода – Домара, которая позволяет анализировать различные сценарии экономического роста в зависимости от динамики совокупного потребления. Рассмотрим простейшую модель экономического развития. Введем обозначения: y(t) – объём выпускаемой продукции; I(t) – объём инвестиций; Р(t) – объём потребляемой продукции [1].
Рассматриваемые объемы исчисляются в рублях. Предположим, что выпуск продукции предусматривает два вида расходов: инвестиции в производство и потребление:
y(t) = I(t) + Р(t). (1)
Слагаемые в уравнении (1) – функции от времени t. Для более наглядного представления уравнение (1) можно выразить в следующем виде:
y = I + Р. (2)
Инвестиции в производство направлены в полном объеме на увеличение капитала ?К = I. С учётом этого уравнение (2) преобразуется:
y = ?К + Р. (3)
Увеличение капиталовложений ?K ведёт к пропорциональному росту объёма выпускаемой продукции:
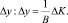 (4)
(4)
Коэффициент пропорциональности  называется коэффициентом приростной капиталоотдачи, при этом имея вид
называется коэффициентом приростной капиталоотдачи, при этом имея вид
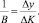 (5)
(5)
Коэффициент приростной капиталоотдачи показывает, на сколько увеличится выпуск продукции ?y при увеличении капиталовложений ?K на единицу.
Преобразуя уравнение (4), можно получить формулу расчета коэффициента приростной капиталоёмкости:
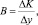
отсюда
?K = B·?y. (6)
Коэффициент приростной капиталоёмкости показывает, на сколько нужно увеличить капиталовложения ?K, чтобы объём выпуска ?y увеличился на единицу.
Если уравнение (3) отнести ко времени ?t, то с учётом уравнения (6) (переходя к пределу) оно преобразуется и примет следующий вид:
y = В·y? + Р. (7)
Полученное линейное дифференциальное уравнение 1-го порядка является моделью экономического роста с учётом потребления (модель Харрода – Домара). Основными характеристиками модели являются:
1. Прирост выпуска пропорционален приросту запаса капитала: 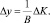
2. Коэффициенты  и В не изменяются во времени [13].
и В не изменяются во времени [13].
В условиях санкционного ограничения потребления можно выделить три сценария экономического роста, различающихся характером динамики потребления:
1 сценарий – потребление отсутствует;
2 сценарий – потребление постоянно во времени;
3 сценарий – потребление растёт с некоторым темпом ?. Для принятия управленческих решений необходимо дать оценку выделенным сценариям [11, 12].
1-й сценарий. Потребление отсутствует: Р = 0. Полученный доход используется на накопление. Ситуация явно неразумная для экономического роста. Однако мы можем использовать модель, которая дает максимально возможный для данной экономики темп роста доходов [7].
Уравнение (7) при Р = 0 упрощается, объём выпускаемой продукции характеризуется:
y = By?. (8)
Получено дифференциальное уравнение 1-го порядка с разделяющимися переменными. При этом 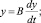
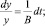
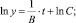
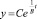 – общее решение дифференциального уравнения [13].
– общее решение дифференциального уравнения [13].
Для расчета показателя – С осуществляется подбор начальных условий и производится частное решение. При t = 0, y = y0, получим C = y0, 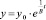 – частное решение дифференциального уравнения, описывающее динамику роста капиталовложений при отсутствии потребления. Динамика роста капиталовложений при отсутствии потребления представлена графически (рис. 1).
– частное решение дифференциального уравнения, описывающее динамику роста капиталовложений при отсутствии потребления. Динамика роста капиталовложений при отсутствии потребления представлена графически (рис. 1).
Темп прироста объема выпускаемой продукции исчисляется по формуле
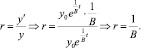
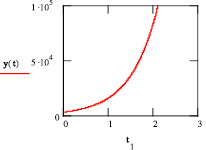
Рис. 1. Динамика роста капиталовложений при отсутствии потребления
Таким образом, максимально возможный темп прироста дохода при его накоплении равен коэффициенту прироста капиталоотдачи  . Поэтому часто коэффициент приростной капиталоотдачи
. Поэтому часто коэффициент приростной капиталоотдачи  называется непрерывным «технологическим» темпом прироста доходов.
называется непрерывным «технологическим» темпом прироста доходов.
2-й сценарий. Сценарий учитывает потребление, которое постоянно во времени, то есть потребление не зависит от времени: Р = Ро = const.
Уравнение (7) при Р = Ро преобразуется следующим образом:
у = By? + Ро. (9)
Это линейное уравнение – 1-го порядка. By? – y + Ро = 0. Его решение осуществляется посредством подстановки y = uv и y? = u?v + uv?. Для начальных условий при t = 0 y = yо получим частное решение дифференциального уравнения:
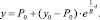 (10)
(10)
Темп прироста
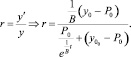 (11)
(11)
Из формулы видно, что с увеличением t (т.е. при t ? ?) 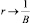 .
.
Это означает, что в предельном случае относительная доля потребления уменьшается до нуля, а темп прироста сравнивается с непрерывным «технологическим» темпом.
График динамики роста капиталовложений по второму сценарию представлен на (рис. 2). По виду он похож на график, представляющий динамику роста капиталовложений при отсутствии потребления (рис. 1). Для сравнения кривая графика экономического роста при отсутствии потребления представлена в виде пунктирной линии.
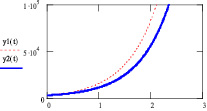
Рис. 2. Динамика роста капиталовложений при постоянном потреблении Р = Ро
3-й сценарий. Потребление растёт с постоянным темпом ?, т.е. 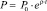 . Модель Харрода – Домара примет вид
. Модель Харрода – Домара примет вид
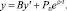 (12)
(12)
При решении уравнения возможны разные варианты.
Вариант 1. Потребление растёт с темпом, равным «технологическому» темпу прироста дохода 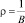 , где
, где
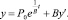 (13)
(13)
Это линейное дифференциальное уравнение, решение которого при начальных условиях при t = 0, у = y0 позволяет получить траекторию роста доходов:
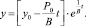 (14)
(14)
Исследуем эту функцию на экстремум. Доход экономики растёт до тех пор, пока уровень накопления остаётся положительной величиной I > 0, из (5) I = By? > 0 ? y? > 0 ? y – возрастает.
Максимальное значение у достигается в точке tmax при у? = 0:
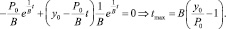 (15)
(15)
Представляет интерес поведение графика функции у после достижения максимума. Проверим, спадает ли производство до полного прекращения выпуска продукции. Для этого приравняем функцию у к нулю и определим точку, в которой это происходит: 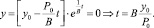
Результаты исследований представлены на графике (рис 3).
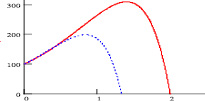
Рис. 3. Динамика развития экономики при высоких темпах потребления
Очевидно, что такой сценарий не может быть рекомендован к исполнению.
Вариант 2. Потребление растёт с темпом, большим, чем технологический темп прироста дохода 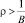 . В этом случае max y достигается быстрее, однако быстрее выпуск продукции снизится до нуля. Такой сценарий более приемлем (рис. 3, пунктиром).
. В этом случае max y достигается быстрее, однако быстрее выпуск продукции снизится до нуля. Такой сценарий более приемлем (рис. 3, пунктиром).
Вариант 3. Потребление растёт с постоянным темпом, меньшим, чем технологический темп прироста дохода Р = Р0·е?t, где 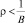 .
.
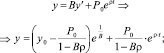 (16)
(16)
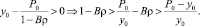
Таким образом, всегда можно подобрать такие значения 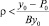 , при которых первое слагаемое в уравнении (16) станет положительным, и тогда доход со временем будет неограниченно возрастать, при неограниченном росте потребления. Это наиболее разумный вариант экономического развития, к которому необходимо стремиться.
, при которых первое слагаемое в уравнении (16) станет положительным, и тогда доход со временем будет неограниченно возрастать, при неограниченном росте потребления. Это наиболее разумный вариант экономического развития, к которому необходимо стремиться.
Модель, предназначенная для анализа различных сценариев экономического роста в зависимости от характера динамики потребления, может быть выражена уравнением
y(t) = B y?(t) + Р(t).
Модель экономического роста при использовании различных сценариев: потребление отсутствует Р(t) = 0; потребление постоянно Р(t) = Рo; потребление растёт с некоторым темпом r, Р(t) = exp(rt).
Практическое применение модели рассмотрим на примере российской экономики. Допустим, что объем выпускаемой продукции равен y0 = 3000 трлн рублей, объем потребляемой продукции 100 трлн, константы: В = 0,6; ? = 0,97; ? = 0,03; t = 0...3,01.
Для каждого из сценариев составим дифференциальные уравнения и исследуем динамику экономического развития, используя для этого пакет Mathcad.
Сценарий 1: Р(t) = 0. Потребление отсутствует. Из
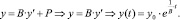
Динамика роста капиталовложений по сценарию представлена графически (рис. 4).
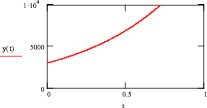
Рис. 4. Динамика роста капиталовложений по сценарию 1
В этом случае достигается максимально возможный темп прироста дохода, который равен коэффициенту приростной капиталоотдачи 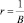 .
.
Сценарий 2. Р = Р0 = const. у = By? + Р0 – Это линейное уравнение – 1-го порядка. Решив его, получим
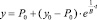 .
.
Видно, что с увеличением t (t ? ?) 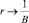 .
.
В отличие от сценария 1, доходы растут медленнее, но экспоненциально. Экономика растет быстро, но вряд ли общество согласится на аскетическое существование без увеличения потребления [5, 9].
Сценарий 3. Потребление растёт с некоторым темпом r, Р(t) = Ро·exp(rt).
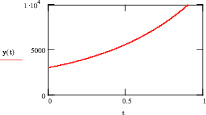
Рис. 5. Динамика роста доходов экономики по сценарию 2
Потребление растёт с постоянным темпом, меньшим, чем технологический темп прироста дохода: Р = Р0·е?t, где 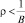 .
.
Модель позволяет проводить исследования по выявлению сценариев, наиболее приемлемых для экономического роста. В расчете для одного из сценариев получен предельный темп роста потребления r = (a0 + e)/В. Если значение e увеличить хотя бы на 0,0001, то график развернется и покажет падение производства до 0 (рис. 6, 7).
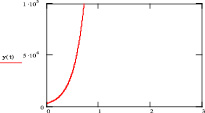
Рис. 6. Динамика роста доходов экономики по сценарию 3 (вблизи критического темпа)
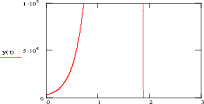
Рис. 7. Динамика роста доходов экономики по сценарию 3
При этом стоит заметить, что краткосрочное прогнозирование экономики на основе роста потребления, даже вблизи критического темпа, позволяет выявлять положительные сдвиги в развитии экономики.
Приближаясь ко второму периоду, без дальнейших преобразований экономики, а лишь только на основе потребления и производства наблюдается спад динамики роста доходов, который в дальнейшем преобразуется в рецессию [8, 10].
Таким образом, построение наиболее простой модели экономического роста Харрода – Домара позволяет сделать следующие выводы.
1. Привлечение инвестиций в экономику страны способствует максимально возможному темпу прироста дохода, который равен коэффициенту приростной капиталоотдачи, что в краткосрочном периоде данный вариант развития экономики характеризует как наиболее рациональный.
2. Резкий рост доходов в экономике возможен на основе статичного потребления. Однако данный вариант, вряд ли сможет удовлетворить потребности общества без увеличения потребления.
3. Только лишь не более чем на два лаговых периода существует возможность поддержания экономического роста (при росте потребления) без привлечения дополнительных ресурсов и внедрения новых экономических стимулов.
Рецензенты:
Чекулина Т.А., д.э.н., профессор кафедры «Бухгалтерский учет, анализ и аудит», ФГБОУ ВПО «Орловский государственный институт экономики и торговли», г. Орёл;
Шапорова О.А., д.э.н., профессор, декан факультета учета и информационных технологий, ФГБОУ ВПО «Орловский государственный институт экономики и торговли», г. Орёл.



