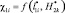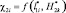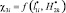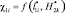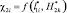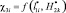С развитием космодромов появились новые виды распределенных внешних систем молниезащит (СМЗ) для ракет-носителей, как для объектов высокоэнергетических и весьма дорогостоящих, удары молний для которых представляют серьезную угрозу при нахождении на стартовых площадках [11]. Примеры современных СМЗ, применяемых на стартовых площадках, их особенности и характеристики представлены в обзоре [8, 9]. Среди них следует выделить типовые молниеприемники составного типа на базе решетчатых металлических башен, в верхних частях которых находятся цилиндрические элементы в виде изоляторов или металлов. Составную конструкцию завершают металлические стержни. На стартовой площадке космодрома такого типа составных молниеприемников СМЗ может быть от 1 до 4 штук [8, 9].
Среди распространенных методов исследований внешних СМЗ следует отметить физическое моделирование на базе высоковольтных лабораторий, например [12]. Такой вид моделирования импульсных электрических разрядов при стартах ракет-носителей, например шаттлов с «Атлантисом» (2006 г.) или с «Индевором» (2009 г.), позволяет относительно легко исследовать прямые удары молний в объекты защиты [12]. Однако чрезвычайно сложно, а вероятнее, невозможно получить результаты физического моделирования при возможных ударах молний в нижнюю часть стартового комплекса, как в случае [11], а не в вершину стержневого молниеприемника СМЗ при нахождении шаттла на старте.
В [10] отмечается, что в настоящее время для изучения нелинейных процессов, связанных с исследованиями атмосферных электрических разрядов, доступны математические модели, представленные в работах Ericsson, Dellera и Garbagnati, Рizk, Becerra и Cooray, в которых определяются каналы разрядов, но не учитываются особенности их разветвления. Для этих целей используются, например, фрактальные подходы [15]. Наряду с этими моделями также широко используются упрощенные методики, методы и различные эмпирические зависимости (например, в [4] представлены их особенности и недостатки). Примеры возможных подходов к расчету внешних СМЗ стартовых площадок представлены, например, в [8, 9, 1, 14].
Цель работы связана с вычислительными экспериментами по исследованию основных особенностей составных молниеприемников СМЗ, применяемых для ракет-носителей в виде металл-изолятор-металл, на основе определения удельного распределения линий функции потока (ЛФП) по поверхностям объектов.
Постановка задачи
За основу принимается метод расчета молниеприемников СМЗ ракет-носителей [1, 14], связанный с вычислением ЛФП в расчетной области на базе вычислительного эксперимента.
Основная расчетная схема некоторой области С(x, y) состоит из составных молниеприемников СМЗ в виде металл-изолятор-металл. Считаем, что такая конструкция в целом образует молниеприемник СМЗ стержневого типа. Они установлены симметрично по углам четырехугольной схемы, а в центре С(x, y) находится ракета-носитель, связанная с технологической мачтой. Такие схемы применяются для стартовых площадок космодромов США, например на Мысе Канаверал, Флорида, стартовые площадки, например, № 40 или № 42 [5]; Франции, Куру, Французская Гвиана [6]; Индии, Шрихорикота (первая стартовая площадка космодрома) [8, 9], французско-российского проекта в Куру [3] и др.
Схема на рис. 1 представлена в вертикальной плоскости, проходящей по диагонали четырехугольной схемы через элементы 1 (один из молниеприемников СМЗ) и элемент 5 (ракета-носитель или технологическая мачта), причем схема симметрична относительно 5. Принимается, что распределенный объект ?0 в области С(x, y) включает элементы 1 (внешняя СМЗ) и 5 (объект защиты). В области С(x, y) составной молниеприемник СМЗ и объект защиты представляются в виде линий, что определяется соотношениями размеров элементов ?0, у которых высоты существенно превышают их боковые размеры (более чем на порядок).
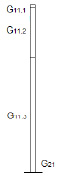
а б
Рис. 1. Схемы области С(x, y) (а) (цифровые обозначения: элемент 1 (молниеприемник) и элемент 5 (ракета-носитель или технологическая мачта)) и составного молниеприемника СМЗ с учетом применения изолятора (б) для границы G11.2
Границы области С(x, y) следующие (рис. 1, а): G21 – граница в виде поверхности земли F(x, y); G22 – некоторая эквипотенциальная линия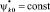 
, как в [1, 14]; G31, G41 – границы для ограничения расчетной области С(x, y); G11, G15 – границы элементов 1 СМЗ и 5 объекта защиты. Для составного молниеприемника считается (рис. 1, б), что G11.3 – это решетчатая металлическая башня; G11.2 – цилиндрический изолятор; G11.1 – металлический стержень с минимальной высотой по отношению к G11.2 и G11.3. Дистанции в расчетной области С(x,y) следующие: l1 – расстояние между молниеприемником 1 и объектом защиты 5; l2 – расстояние между объектом защиты 5 и боковой границей G31 области С(x,y).
Для сопоставительного анализа составных типов молниеприемников СМЗ стартовых площадок рассмотрим 2 варианта с учетом применения изолятора или металлического элемента в его средней части (граница G11.2). Доказательства возможности перехода от решения внешней краевой задачи к внутренней даны в [13] и применимы в этой работе.
Вариант 1. Проводятся вычислительные эксперименты с возможностью определения основных особенностей составных молниеприемников с учетом применения изолятора в его средней части (рис. 1, б). Тогда для этого варианта будет исследоваться объект ?01, т.е. с молниеприемником СМЗ и с учетом изолятора (G11.2).
Поле электрической функции потока µi определяется из уравнения эллиптического типа (1) по виду аналогичного уравнения Лапласа, при этом следует заметить, что граничные условия для функций µ и ? существенно различаются:
?2µ/?x2 + ?2µ/?y2 = 0; (x, y) ? С(x, y). (1)
Граничные условия задачи c учётом рис. 1 следующие:
? на границе G31:
µ(x, y) = µ01, (x, y) ? G31; (2)
? на границе G41:
µ(x, y) = 0, (x, y) ? G41; (3)
? на левой боковой границе G11.2 (изолятора):
µ(x, y) = µ01, (x, y) ? G11.2; (4)
? на правой боковой границе G11.2 (изолятора):
µ(x, y) = 0, (x, y) ? G11.2; (5)
? на границе G21:
?µ/?n = 0, (x, y) ? G21; (6)
? на границах G11.3 и G11.1 (металлические элементы молниеприемника 1):
?µ/?n = 0, (x, y) ? G11.3, G11.1; (7)
? на границе G15 (объект защиты 5):
?µ/?n = 0, (x, y) ? G15; (8)
? на границе G22:
µ(x, y) = 0, (x, y) ? G22; (9)
где С(x, y) – исследуемая область и ограничена G11.1, G11.2, G11.3, G21, G22, G31, G41, G15.
Для оценки и сравнительного анализа особенностей распределенных объектов ?0i считаем, что ЛФП электростатического поля в виде линий семейства µi(x, y) = const начинаются со стороны границы G23.
Тогда на границе G23 записывается условие вида
?µ/?n = 0, (x, y) ? G23. (10)
На основной части границы G22 выполняется условие (9).
Вариант 2. Вычислительные эксперименты проводятся для определения особенностей составных металлических молниеприемников СМЗ (рис. 1, а). Тогда для этого варианта будет исследоваться объект ?02, т.е. с цельнометаллическим молниеприемником СМЗ.
Поле функции потока µi также определяется из уравнения эллиптического типа (1).
Тогда граничные условия этой задачи c учётом рис. 1, а следующие:
? на границе G21:
?µ/?n = 0, (x, y) ? G21; (11)
? на границах G11 (молниеприемник 1) и G15 (объект защиты 5):
?µ/?n = 0, (x, y) ? G11, G15; (12)
? на границе G31:
µ(x,y) = µ01, (x, y) ? G31; (13)
? на границе G41:
µ(x, y) = 0, (x, y) ? G41; (14)
? на границе G22:
µ(x, y) = 0, (x, y) ? G22; (15)
где С(x, y) – исследуемая область и ограничена G21, G22, G31, G41, G11, G15.
Применяется аналогичная граница G23 на краю G22. Считаем, что ЛФП (в виде линий семейства µi(x, y) = const) начинаются с G23. На ней записывается условие вида
?µ/?n = 0, (x, y) ? G23, (16)
тогда на оставшейся части границы G22 выполняется условие (15).
Допущения следующие. Считается, что внешнее поле по отношению к объектам ?0i относительно мало, т.е. подход справедлив до начала коронного разряда в грозовых облаках и при отсутствии объёмных электрических зарядов в атмосфере исследуемой области С(x, y).
Результаты расчетов и сравнительный анализ
Результаты расчетов представляются в безразмерном виде
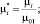
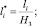
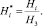(17)
Приняты нормирующие значения: для функции потока – µ01; для дистанций и высот в расчетной области С(x, y) – H3, т.е. исходная высота объекта защиты 5. Остальные величины нормируются аналогичным образом.
Для вариантов краевых задач с учетом их математических моделей в виде уравнения эллиптического типа (1) с соответствующими граничными условиями, с использованием итерационного метода верхней релаксации и на основе разработанных программных средств проведем вычислительные эксперименты для определения удельного распределения ЛФП относительно исследуемых элементов ?0i в расчетной области С(x, y). Например, расчет уединенного стержневого молниеприемника в трехмерной области дан в [14] с использованием итерационного метода верхней релаксации.
Для варианта 1 в области С(x, y) с учетом исследуемых элементов ?01 стартовых площадок принимаются следующие условия: дистанция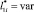 
является независимой величиной и изменяется с заданным шагом. Высота объекта защиты 5 принимается 
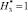, а относительная высота молниеприемника СМЗ задается в виде 
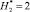и также является независимой величиной при вычислительных экспериментах. Следует отметить, что при исследованиях соотношений высот составного молниеприемника его части могут изменяться, т.е. 
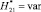(граница G11.1), 
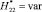(граница G11.2), 
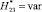(граница G11.3). Высота до некоторой эквипотенциальной линии 
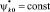принимается 
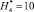(вместо некоторой исходной границы V(x, y) [1, 14]).
Приняты следующие обозначения: ?1i – величина удельного распределения ЛФП объекта защиты 5 (т.е. элемента ?01) или представляется в виде функции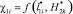 
; ?2i – величина удельного распределения ЛФП по F(x, y) в области С(x,y) или в виде 
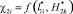; ?3i – величина удельного распределения ЛФП для молниеприемника СМЗ (т.е. элемента ?01) или в виде 
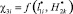. Результаты вычислительного эксперимента, полученные с учетом независимых величин 
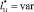и при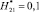 
; 
; 
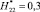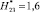, т.е. в целом при 
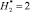(ni = 100), сведены в табл. 1.
Для варианта 2 в области С(x, y) с учетом исследуемых элементов ?02 стартовых площадок принимаются аналогичные условия: дистанция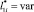 
является независимой величиной и изменяется с заданным шагом. Высота объекта защиты 5 принимается 
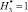, а относительная высота молниеприемника СМЗ задается в виде 
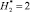и также является независимой величиной при вычислительных экспериментах. Высота до некоторой эквипотенциальной линии 
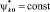принимается 
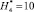(вместо некоторой исходной границы V(x, y) [1,14]). Обозначения для ?i аналогичные. Результаты вычислительного эксперимента, полученные с учетом независимых величин 
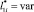и при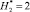 
(ni = 100), сведены в табл. 2.
Таблица 1
Удельное распределение ЛФП ?i в области С(x, y) при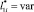 
с учетом H*21 = 0,1 (G11.1), 
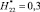(G11.2), 
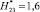(G11.3), т.е. при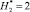 
|
?i – величина исследуемого элемента в С(x, y) |
Дистанция |
|||||||
|
0,8 |
1,2 |
1,6 |
2,0 |
2,4 |
2,8 |
3,2 |
3,6 |
|
|
?1i |
0,0 |
0,022 |
0,035 |
0,050 |
0,062 |
0,073 |
0,084 |
0,095 |
|
?2i |
0,145 |
0,114 |
0,090 |
0,076 |
0,065 |
0,067 |
0,084 |
0,115 |
|
?3i |
0,855 |
0,864 |
0,875 |
0,874 |
0,873 |
0,860 |
0,832 |
0,790 |
до молниеприемника СМЗТаблица 2
Удельное распределение ЛФП ?i в области С(x,y) пр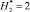и 
и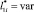 
|
?i – величина исследуемого элемента С(x, y) |
Дистанция |
||||||||
|
0,8 |
1,2 |
1,6 |
2,0 |
2,4 |
2,8 |
3,2 |
3,6 |
4,0 |
|
|
?1i |
0,030 |
0,060 |
0,090 |
0,120 |
0,145 |
0,165 |
0,180 |
0,195 |
0,200 |
|
?2i |
0,300 |
0,230 |
0,175 |
0,150 |
0,145 |
0,175 |
0,220 |
0,285 |
0,380 |
|
?3i |
0,670 |
0,710 |
0,735 |
0,730 |
0,710 |
0,660 |
0,600 |
0,520 |
0,420 |
до молниеприемника СМЗ
a б в
Рис. 2. Результаты расчета линий семейства µi(х, у) = const для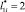 
, 
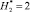, ni = 30: а – расчетная схема 
, 
, 
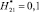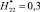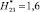(высоты молниеприемников для 2-х вариантов равны 
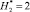); б – вариант 1; в – вариант 2
Типичный пример результатов расчета ЛФП для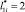 
, 
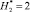, но при условии ni = 30 (т.е. это количество ЛФП в С(x, y)) для исследуемых вариантов показан на рис. 2. Из рисунка следует, что количество ЛФП, замыкающихся на составных молниеприемниках в виде металл-изолятор-металл, существенно больше, чем на металлических молниеприемниках.
Результаты вычислительных экспериментов для 2-х вариантов, полученные с учетом независимых величин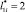 
и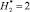 
(ni = 100), сведены в табл. 3.
Результаты вычислительных экспериментов для этих же вариантов, полученные с учетом независимых величин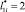 
и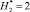 
, но при ni = 30, т.е. при существенном уменьшении количества ЛФП в сравнении с табл. 3, представлены в табл. 4.
Таблица 3
Удельное распределение ЛФП ?i в области С(x,y) пр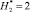и 
и 
|
Исследуемые варианты |
?i – величина исследуемого элемента в С(x,y) |
||
|
|
|
|
|
|
Вариант 1 |
0,050 |
0,076 |
0,874 |
|
Вариант 2 |
0,120 |
0,150 |
0,730 |
Таблица 4
Удельное распределение ЛФП ? i в области С(x,y) пр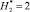и 
и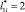 
|
Исследуемые варианты |
?i – величина исследуемого элемента в С(x,y) |
||
|
|
|
|
|
|
Вариант 1 |
0,050 |
0,080 |
0,870 |
|
Вариант 2 |
0,117 |
0,183 |
0,700 |
Анализ результатов табл. 3 показывает, что при использовании составного молниеприемника СМЗ в виде металл-изолятор-металл существенно увеличивается эффективность перехвата молний внешними СМЗ по варианту 1 в сравнении с вариантом 2. За критерий перехвата молний условно принимается величина удельного распределения ЛФП для ?0i в области С(x, y). Например, пр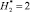и 
и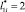 
(вариант 1) получается результат, при котором функция 
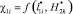объекта защиты (т.е. одного из элементов ?0i) уменьшилась в 2,4 раза по сравнению с составным металлическим молниеприемником СМЗ, при этом функция 
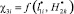для молниеприемника СМЗ (также элемента ?0i) увеличилась в 1,2 раза (т.е. практически достигла максимума). Сравнительнительный анализ данных вычислительных экспериментов, представленных в табл. 3 и 4, показывает, что при уменьшении ni до 30, т.е. при существенном уменьшении количества ЛФП, а именно более чем 3,3 раза, полученные результаты хорошо коррелируют между собой. Максимальная абсолютная ошибка находится в пределах ? ? |0,03|.
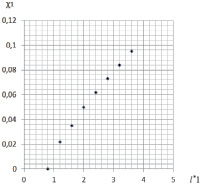
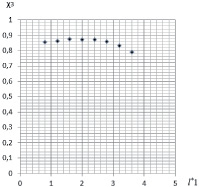
На основе результатов табл. 1 представим основные характеристики ?1i и ?3i для распределенного ?01 (рис. 3), а также для ?2i в области С(x, y) (рис. 4). Характеристики представлены в дискретном виде для необходимости соблюдения закона сохранения заряда.
Анализ характеристик на рис. 3 и 4 показывает, что эти функции вида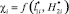 
являются нелинейными. Тогда согласно принятому подходу считается, что 
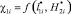применяется для оценки объекта защиты на основе удельного распределения ЛФП в расчетной области С(x, y), а 
– для оценки составных молниеприемников СМЗ. В связи с этим на базе вычислительных экспериментов имеется возможность установить оценочный критерий определения эффективности перехвата молний для различных схем СМЗ стартовых площадок на основе удельного распределения ЛФП для ?0i в области С(x, y).
Следовательно, чем больше величина удельного распределения ЛФП на молниеприемниках СМЗ и существенно меньше на объектах защиты, тогда будет выше эффективность перехвата молний для исследуемых схем стартовых площадок космодромов, на базе распределенных молниеприемников СМЗ для ракет-носителей.
Сравнительный анализа результатов на рис. 3 и 4 показывает, что все функций вида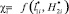 
являются нелинейными. Следует также отметить (табл. 2), что наблюдается корреляция с данными на рис. 3, а именно величина удельного распределения ЛФП на молниеприемниках СМЗ существенно больше, чем на объектах защиты. Исследования составных молниеприемников с учетом применения изоляторов проводились, например, в [2], но на базе решения классической задачи электростатики с применением уравнения Лапласа.
a б
Рис. 3. Результаты расчета удельного распределения ЛФП при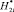 
и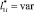 
(ni1 = 100): величина ?1 объекта защиты (a) и величина ?3 элемента внешней СМЗ (б)
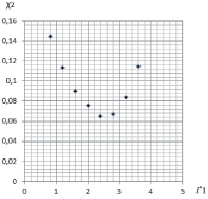
Рис. 4. Результаты расчета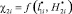 
для F(x, y) при 
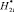и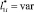 
(ni1 = 100)
Сравнение полученных результатов с [2] показывает, что данные [2] подтверждают, причем на основе анализа относительных величин напряженности электростатического поля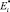 
для составных молниеприемников с изоляторами и тросами в сравнении с 
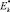для составных цельнометаллических молниеприемников также с тросами [2], что 
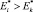. Следовательно, получен один и тот же результат, но с разными подходами. Однако получение решения для известного эффекта [11] на базе данных [2] практически затруднено ввиду отсутствия критерия для этого анализа.
Анализ функции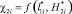 
(рис. 4) показывает следующее, что эта характеристика нелинейная и имеет вид некоторой параболической зависимости с минимумом при 
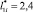. Следует отметить, что эта функция 
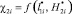представляет удельное распределение ЛФП по поверхности земли в расчетной области С(x, y). В связи с этим она не представляет особой важности для исследуемого распределенного объекта ?0i. Однако эта функция позволяет обосновать существование экспериментальных эффектов, связанных с ударами молний не только в вершины объектов, но и в боковые их части, а также в поверхность F(x,y), на которой они расположены [11].
Кроме того, известна схема с 4-мя стержневыми молниеприемниками СМЗ для ракет-носителей типа «Антарес» (США) [7]. В этой схеме молниеприемники располагаются на относительно минимальных дистанциях от корпуса ракеты-носителя, так как они имеют цилиндрическую форму. Данные [7] косвенно подтверждают полученные результаты на основе вычислительных экспериментов для составных молниеприемников СМЗ стартовых площадок. А именно, согласно расчетам при уменьшении дистанции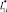 
функция 
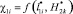объекта защиты стремится к минимуму, а функция 
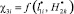молниеприемника СМЗ стартовой площадки стремится к некоторому относительно максимальному значению. В связи с этим для внешних СМЗ ракет-носителей типа «Антарес» молниеприемники располагаются на минимальных дистанциях от корпуса ракеты-носителя.
Выводы
1. В результате расчетов на основе двумерной модели установлено, что составные молниеприемники металл-изолятор-металл являются более эффективными при перехвате молний в сравнении с полностью металлическими составными молниеприемниками. Анализ основан на косвенных данных о применении семейства линий функций потока (ЛФП) для распределенных объектов, находящихся в атмосферном электростатическом поле, при вычислении удельного распределения ЛФП в условиях отсутствия коронных разрядов в исследуемой области. Полученные данные в дальнейшем будут уточняться с более детальным моделированием и на базе применения трехмерной модели.
2. При вычислительных экспериментах показано, что определяемые величины удельного распределения ЛФП для составных молниеприемников с применением и без изоляторов являются нелинейными, причем их экстремумы не совпадают.
3. Выявлено, что функция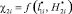 
в виде удельного распределения ЛФП по поверхности земли в области С(x, y) может применяться для косвенного обоснования экспериментальных эффектов, связанных с ударами молний не только в вершины объектов, но и в боковые их части, а также в поверхность F(x, y), на которой они расположены.
Рецензенты:
Лесовик Р.В., д.т.н., профессор, проректор по международной деятельности, ФГБОУ «Белгородский государственный технологический университет им. В.Г. Шухова», г. Белгород;
Шаптала В.Г., д.т.н., профессор кафедры защиты в чрезвычайных ситуациях, Институт СМ и техносферной безопасности, ФГБОУ «Белгородский государственный технологический университет им. В.Г. Шухова», г. Белгород.