Нелинейно-оптические методы диагностики материалов, основанные на различных механизмах светоиндуцированной модуляции оптических констант среды, широко используются в аналитической химии [2, 8, 10–12, 14]. Светоиндуцированное изменение концентрации полимерных наночастиц приводит к соответствующей модуляции оптических свойств среды. Это позволяет реализовать различные модификации оптического бесконтактного контроля параметров наночастиц практически в реальном времени. Например, метод тепловой линзы используется в термооптической спектрометрии, в оптической диагностике материалов [4–7]. В жидких двухкомпонентных средах термолинзовый отклик имеет свои особенности, поскольку кроме обычного теплового отклика, связанного с тепловым расширением среды, здесь могут возникать концентрационные потоки, обусловленные явлением термодиффузии (эффект Соре) [1–2].
Целью данной работы является теоретический анализ термодиффузионного вклада в формирование линзы в двухкомпонентной среде под действием пучка излучения с равномерным профилем интенсивности в ограниченной кювете.
Рассмотрим двухлучевую термолинзовую схему (рис. 1): на кювету с двухкомпонентной средой (наножидкостью) падает опорный пучок с равномерным профилем интенсивности I0, формирующий температурное поле. Образованная в среде линза тестируется сигнальным гауссовым пучком c другой длиной волны. Для определения величины термодиффузионной линзы рассмотрим систему балансных уравнений, описывающих процессы, возникающие при воздействии светового поля с бинарной смесью [5]:
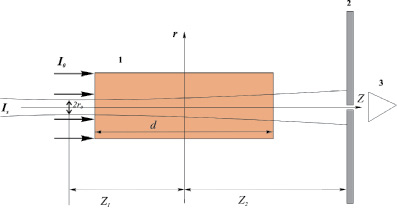
Рис. 1. Двухлучевая термолинзовая схема
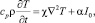 (1)
(1)
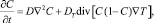 (2)
(2)
где T – температура среды; C(r, t) – массовая концентрация наночастиц; ? – коэффициент теплопроводности среды; cp, ? – соответственно удельные теплоемкость и плотность жидкости; ? – коэффициент поглощения излучения; I0 – интенсивность падающего излучения светового пучка; D и DT – коэффициенты диффузии и термодиффузии.
В стационарном случае 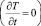 уравнение (1) принимает вид
уравнение (1) принимает вид
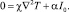 (3)
(3)
Будем рассматривать случай малых концентраций (C << 1) и малых ее изменений, тогда уравнение (2) в стационарном режиме принимает вид
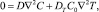 (4)
(4)
где C0 – начальная концентрация частиц.
С учетом подстановки (3) уравнение (4) преобразуется:
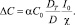 (5)
(5)
В дальнейшем, переходя к цилиндрическим координатам, имеем задачу
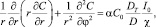
0 ? r ? R; (6)
C(R) = C0, (7)
где ? – полярный угол в плоскости перпендикулярной оси Z; R – радиус цилиндрической кюветы.
Решение задачи (6)–(7) получаем с учетом существования конечной производной 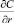 при r = 0 и независимости концентрации от угла ?:
при r = 0 и независимости концентрации от угла ?:
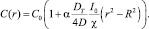 (8)
(8)
Решая аналогичным способом тепловую задачу (3) с учетом T(R) = T0, где T0 – температура на границе кюветы, получаем
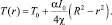 (9)
(9)
Термолинзовый сигнал ?(t) показывает изменение интенсивности, регистрируемое фотоприемником за экраном:
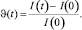 (10)
(10)
Для расчета термолинзового сигнала используем выражение для линзовой прозрачности кюветы [15]:
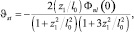 (11)
(11)
где Z1, Z2 – расстояния от центра кюветы до перетяжки гауссова пучка и до экрана соответственно (рис. 1), 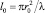 ; r0 – радиус перетяжки гауссова пучка; ?nl(0) – нелинейный набег фаз в оптической ячейке на оси пучка.
; r0 – радиус перетяжки гауссова пучка; ?nl(0) – нелинейный набег фаз в оптической ячейке на оси пучка.
Нелинейный набег фаз складывается из двух вкладов – теплового расширения дисперсной фазы и концентрационного, связанного с изменением концентрации дисперсных частиц:
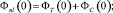 (12)
(12)
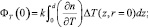 (13)
(13)
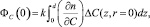 (14)
(14)
где 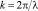 – волновой вектор излучения зондирующего пучка Is.
– волновой вектор излучения зондирующего пучка Is.
Интегрируя (13) и (14) получаем
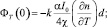 (15)
(15)
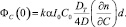 (16)
(16)
Таким образом можно получить величину стационарного термолинзового сигнала:
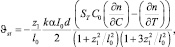 (17)
(17)
где 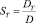 – параметр Соре.
– параметр Соре.
Рассмотрим отношение двух вкладов 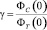 :
:
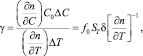 (18)
(18)
где 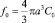 – начальное значение объемной доли нанофазы. Здесь учтено, что параметр
– начальное значение объемной доли нанофазы. Здесь учтено, что параметр 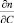 можно найти как
можно найти как
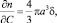 (19)
(19)
где n1, n2 – показатели преломления жидкости и дисперсной сред соответственно; V – объем частиц, ? = n1 – n2; a – радиус частиц.
Экспериментальные данные показывают, что, как правило, коэффициент Соре для наночастиц прямо пропорционален их размеру [13]. Температурный коэффициент 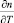 для большинства жидкостей лежит в диапазоне 2?10–4...6?10–4 K–1. На рис. 2 показаны графики зависимости ? от коэффициента Соре для f0 = 10–2 и f0 = 10–3;
для большинства жидкостей лежит в диапазоне 2?10–4...6?10–4 K–1. На рис. 2 показаны графики зависимости ? от коэффициента Соре для f0 = 10–2 и f0 = 10–3; 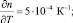 ? = 10–2.
? = 10–2.
Из графиков видно, что для достаточно больших наночастиц (с радиусом около 100 нм) и при значительных объемных долях концентрационный вклад в термолинзовый отклик сравним с таковым для жидкости.
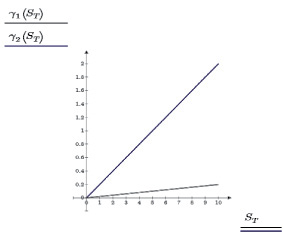
Рис. 2. Зависимости ? от коэффициента Соре для f0 = 10–2 (--) и f0 = 10–3 (--)
Таким образом, в работе получено выражение для стационарного термолинзового отклика двухкомпонентной среды, обусловленного термодиффузией. Результаты представляют интерес для термолинзовой спектрометрии многокомпонентных сред [14], оптической диагностики, а также нелинейной адаптивной оптики [3–6, 9].
Рецензенты:
Карпец Ю.М., д.ф.-м.н., профессор кафедры «Физика и теоретическая механика», ФГОУ ВПО «Дальневосточный государственный университет путей сообщения», г. Хабаровск;
Криштоп В.В., д.ф.-м.н., профессор кафедры «Физика и теоретическая механика», проректор по учебной работе, ФГОУ ВПО «Дальневосточный государственный университет путей сообщения», г. Хабаровск.



