МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ ДВУХМАССОВОГО ВИБРАЦИОННОГО МОБИЛЬНОГО РОБОТА
1
Яцун С.Ф. 1 Яцун А.С. 2 Ворочаева Л.Ю. 2
1 ФГБОУ ВО «Юго-Западный государственный университет»
2 ФГБОУ ВО «Юго-Западный государственный университет»
В работе рассмотрена система очистки трубопроводов на базе мобильного вибрационного робота, состоящего из двух секций, связанных между собой упруго-вязким элементом и электроприводами. Одна из секций снабжена рабочим инструментом, позволяющим производить очистку внутренней поверхности трубопровода, твердые отложения в которой моделируются упруго-вязкой моделью Кельвина ? Фойгта. Секции робота совершают движение друг относительно друга, в результате этого за счет управляемого трения на контакте секций и внутренней поверхности трубы робот перемещается по шероховатой поверхности. Разработана математическая модель, описывающая движение устройства при взаимодействии робота и твердых отложений, в качестве привода в которой рассматривается электромагнит, исследован ударный режим движения устройства, получена зависимость средней скорости поступательного перемещения системы от частоты внешнего периодического управляющего напряжения.
вибрация
удар
мобильный робот
очистка
трубопровод
собственные частоты
резонанс
1. Болотник Н. Н. Динамика управляемых движений вибрационных систем / Н.Н. Болотник, И.М. Зейдис, К. Циммерман, С.Ф. Яцун // Изв.РАН. ТиСУ. – 2006. – № 5. – С. 1–11.
2. Волкова Л.Ю. Исследование динамики вибрационного инструмента при его взаимодействии с обрабатываемой средой / Л.Ю. Волкова, И.В. Лупехина, Г.Я. Пановко, С.Ф. Яцун // Машиностроение и инженерное образование. – 2010. – № 4. – С. 63–72.
3. Ворочаева Л.Ю. Моделирование движения трехзвенного робота с управляемыми силами трения по горизонтальной шероховатой поверхности / Л.Ю. Ворочаева, Г.С. Наумов, С.Ф. Яцун // Изв.РАН. ТиСУ. – 2015. – № 1. – С. 156–170.
4. Гранкин А.Н. Исследование виброударных режимов движения мобильного микроробота с электромагнитным приводом / А.Н. Гранкин, С.Ф. Яцун // Изв.РАН. ТиСУ. – 2009. – № 1. – С. 163–171.
5. Мальчиков А.В. Вибрационный мобильный микроробот / А.В. Мальчиков, С.Ф. Яцун // Робототехника и техническая кибернетика. – 2014. – № 3 (4). – С. 64–68.
6. Черноусько Ф.Л. Влияние сил трения на динамику двузвенного мобильного робота / Ф.Л. Черноусько, М.М. Шундерюк // ПММ. – 2010. – Т. 74. – Вып. 1. – С. 22–36.
7. Яцун А.С. Динамика управляемого движения мобильного ползающего робота с изменяемой формой корпуса: автореф. дис. ... канд. техн. наук. – Орел, 2012. – 24 с.
8. Jatsun S.F. Dynamics of the vibration driven tool at its interaction with the processing material / S.F. Jatsun, I.V. Lupehina, G. Ja. Panovko, L.Yu. Volkova / 13th World Congress in Mechanism and Machine Science. – Guanajuato, M xico, 2011. – P. 1–5.
Очистка сточных вод машиностроительных предприятий, содержащих значительное количество отработанных смазочно-охлаждающих жидкостей, связана с большими техническими трудностями и серьёзными материальными затратами. Проблема осложняется тем, что трубопроводные системы очень быстро загрязняются твердыми отложениями, которые поддаются только механической очистке.
Роботы, перемещающиеся внутри труб, отличаются по конструкции и принципу движения. Наиболее распространенными являются многозвенные змее- и червеподобные роботы с изменяемой геометрией [3, 6, 7]. Взаимодействие таких устройств с поверхностью трубопровода осуществляется специальными опорами, как правило с управляемым трением, что позволяет одним секциям робота фиксироваться в трубе, а другим перемещаться вперед относительно неподвижных звеньев. Помимо этого часто для движения по трубам используются вибрационные роботы, перемещающиеся по поверхности за счет движения внутренних масс [1, 4, 5]. Данные системы обычно оснащены управляемыми опорными элементами с асимметричным трением.
В настоящей работе для очистки внутренних поверхностей трубопроводов предлагается использовать вибрационные мобильные робототехнические устройства, которые могут автономно передвигаться внутри трубопровода, взаимодействуя с внутренней поверхностью трубы непосредственно своим корпусом, а установленный на таком транспортном модуле режущий элемент способен очистить поверхность трубы достаточно эффективно. Применение вибрационных роботов в качестве инструментов, взаимодействующих с технологической средой, описано в работах [2, 8]. Рассматриваемый виброинструмент оснащен дебалансным электроприводом, а обрабатываемая среда представлена упруго-вязко-пластической моделью. В данной работе особое внимание уделено разработке математических моделей, описывающих сложные динамические процессы, протекающие в вибрационных мобильных робототехнических устройствах, с учетом взаимодействия режущего элемента с твердыми загрязнениями.
Описание вибрационного робота
В работе рассматривается поведение вибрационной системы, состоящей из двух твердых тел, причем оба тела контактируют с шероховатой поверхностью. Тела связаны между собой управляемым электроприводом, которым в частном случае является электромагнит, под действием которого тела совершают колебательное движение. Для получения поступательного движения робота по шероховатой поверхности каждое тело снабжено устройством асимметричного трения, обеспечивающим перемещение тела только в одном направлении. Такого эффекта можно достигнуть, например, снабжая контактные поверхности робота специальными шариковыми заклинивающими элементами, образующими фрикционные механизмы с управляемым трением. Общий вид вибрационной системы приведен на рис. 1, а. Массы системы 1 и 2 связаны между собой упругим элементом 3. Каждое тело снабжено механизмами 4, обеспечивающими асимметрию силы трения между массами и опорной поверхностью. Электромагнитный привод состоит из сердечника с катушкой 5, установленного на теле 1 и якоря 6, закрепленного на теле 2. Рабочий орган, представляющий собой механический скребок 7, счищает накопившиеся отложения 8 внутри трубы.
Движение системы происходит за счет периодического сближения тел под действием силы электромагнитного привода. Под действием электромагнитной силы тело 1 приближается к телу 2, которое благодаря наличию асимметричного механизма 4 останавливается. После отключения электрического питания электромагнита под действием пружины 3 тело 2 отходит от тела 1, которое, в свою очередь, остается на месте благодаря работе собственного механизма 4. Таким образом происходит перемещение центра масс системы.
Математическая модель мобильного вибрационного робота
Расчетная схема исследуемой системы представлена на рис. 1, б.
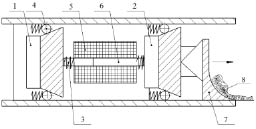
а
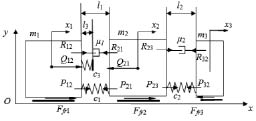
б
Рис. 1. а – общий вид вибрационного устройства для внутренней очистки трубопроводов; б – расчетная схема робота
Движение устройства происходит в вертикальной плоскости Оху вдоль оси Ох. Массы 1 и 2 робота представляют собой абсолютно твердые тела массами m1 и m2, движение каждой из них вдоль оси Ох описывается обобщенной координатой х1 и х2. Геометрическими размерами и формой тел пренебрегаем. Для соединения масс между собой используется упруго-вязкий элемент с жесткостью пружины с1, ее длиной в недеформированном состоянии
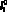
и коэффициентом вязкого сопротивления µ1. Помимо этого между телами присутствует упругий ограничитель с недеформированной длиной
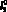
и жесткостью с3, причем с3 > > с1. Среда, действующая на массу 2 робота, представлена абсолютно твердым телом массой m3, их взаимодействие описывается моделью Кельвина ? Фойгта с параметрами с2, µ2 и длиной недеформированной пружины
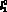
.
На массу m1 действуют силы электромагнитного привода Q12, упругого элемента P12, вязкого сопротивления R12. На массу m2, соответственно, действуют силы: Q21, P21, R21. Очевидно, что эти силы попарно равны по модулю и противоположны по знаку. Помимо этого на массу m2 со стороны среды действуют силы упругости P23 и вязкого сопротивления R23. Масса m3 находится под действием сил упругости P32 и вязкого сопротивления R32, приложенных со стороны массы m2. Кроме этих сил при взаимодействии каждой из масс с поверхностью возникают силы трения Ffr1, Ffr2, Ffr3.
В качестве задающего воздействия выступают периодические силы Q12 и Q21. Эти силы являются внутренними и вызывают вибрационное движение масс m1 и m2 относительно центра масс системы. Движение центра масс происходит в результате того, что силы трения, действующие на массы 1 и 2, являются внешними и имеют разные модули в зависимости от направления скорости, что приводит к возникновению поступательного движения робота в положительном направлении по оси Оx.
Запишем систему дифференциальных уравнений, описывающих движение масс системы:
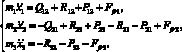 (1)
(1)
Здесь точками обозначены производные по времени от обобщенных координат.
В рассматриваемой схеме упругий элемент между телами 1 и 2 выполнен кусочно-линейным с жесткостями с1 и с3. Дополнительная пружина с жесткостью с3 включается в работу в зависимости от расстояния l1 между массами и величиной l3. Значение деформации ?l3 определим следующим образом:
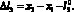 (2)
(2)
Деформация основной пружины с жесткостью с1 равна
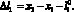 (3)
(3)
Если l1 > l3, то деформируется только пружина с жесткостью с1 и имеет место безударный режим движения. В противном случае, когда l1 ? l3, происходит скачкообразное изменение жесткости, что приводит к быстрому изменению скорости массы m2 и рабочего инструмента, поэтому такое движение можно отнести к виброударному.
Сила упругого сопротивления между телами 1 и 2 вычисляется по формуле
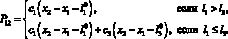 (4)
(4)
Для силы Р23 справедлива формула
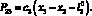 (5)
(5)
Силы вязкого сопротивления записываются следующим образом:
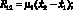
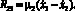 (6)
(6)
Сила трения представлена моделью [1]:
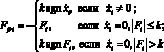 , (7)
, (7)
здесь k = fNi;, i = 1–3; f – коэффициент трения; Ni – нормальная реакция i-й массы; Fi – горизонтальная проекция равнодействующей всех сил, кроме силы сухого трения, приложенных к массе.
Коэффициент трения принимает два значения f+ и f– в зависимости от знака скорости движения массы, причем f+ << f–:
 (8)
(8)
Силы, действующие на массы со стороны электромагнитного привода, определяются по формуле
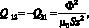 (9)
(9)
где Ф – магнитный поток, возникающий в магнитном контуре сердечника; µ0 – магнитная проницаемость; S – площадь воздушного зазора; z – число витков проводника с током. Для определения магнитного потока Ф запишем следующее уравнение:
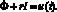 (10)
(10)
Данное уравнение устанавливает связь меж ду напряжением электрического питания u(t) и магнитным потоком Ф, током I и активным сопротивлением катушки электромагнита r.
Ток, возникающий в электрической цепи, определим по формуле
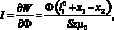 (11)
(11)
где W – магнитная энергия.
Рассмотрим случай подачи на катушку периодического электрического напряжения с амплитудой U0 и частотой ?. Напряжение u(t) будем моделировать следующим образом:
 (12)
(12)
Система уравнений, описывающая движение масс вибрационной системы, имеет вид
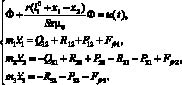 (13)
(13)
Результаты моделирования движения робота
В результате моделирования движения робота путем численного решения системы дифференциальных уравнений (13) получены временные графики перемещений и скоростей масс системы для ударного режима (рис. 2, 3).
а б
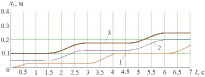
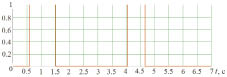
Рис. 2. а – графики перемещений тел системы; 1 – первого, 2 – второго, 3 – третьего; б – моменты включения/выключения упругого ограничителя
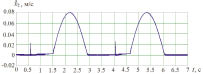
а б
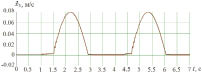
в
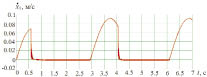
Рис. 3. Графики скоростей тел системы: а – первого, б – второго, в – третьего
На рис. 2, б приведена временная зависимость включения/выключения упругого ограничителя. Моделирование проводится для устройства, массы которого равны m1 = m2 = m3 = 0,01 кг, жесткость пружин с1 = с2 = 200 Н/м, с3 = 500 Н/м, коэффициенты вязкого сопротивления µ1 = µ2 = 0,1 Нс/м.
По графикам перемещения (рис. 2, а) видно, что движение тел системы происходит в положительном направлении оси Ох и представляет собой чередование зон перемещения и зон покоя. Причем движение тела 1 происходит при неподвижно зафиксированном на поверхности теле 2, и наоборот. Временные зависимости перемещения массы 2 робота и технологической нагрузки имеют одинаковый характер, но смещены друг относительно друга на расстояние, равное длине недеформированной пружины между телами 2 и 8.
По графикам скоростей (рис. 3) видно, что движение системы происходит в ударном режиме. Это подтверждается тем, что в моменты включения упругого ограничителя (рис. 2, б) останавливается тело 1, его скорость скачкообразно уменьшается до нулевой, а тело 2 приобретает мгновенную скорость во время удара, которая затем так же резко обнуляется. При выключении упругого ограничителя тело 2 приходит в движение. Зависимости скоростей тел 2 и 3 повторяют друг друга, отличие заключается в том, что на графике скорости тела 3 нет скачка в момент срабатывания упругого элемента между телами 1 и 2.
Для исследуемой системы построен график зависимости средней скорости ее движения vsr от частоты ? напряжения электромагнитного привода, приведенный на рис. 4. По данной кривой видно, что средняя скорость системы плавно возрастает по мере увеличения частоты ? до достижения ею значения 520 рад/с. Затем наблюдается плавное убывание vsr практически до нулевого значения. Следовательно, для обеспечения движения робота с большой средней скоростью необходимо, чтобы частота напряжения электромагнита находилась в диапазоне 520 ± 10 рад/с.
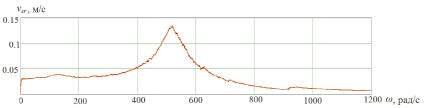
Рис. 4. График зависимости средней скорости движения системы от частоты напряжения электромагнитного привода
В статье рассмотрен внутритрубный робот, взаимодействующий с технологической нагрузкой, моделируемый в виде двухмассовой вибрационной системы при наличии асимметричного сухого трения на контакте масс и шероховатой поверхности. Для ударного режима движения получены графики перемещений и скоростей масс системы, а также зависимость средней скорости движения устройства от частоты напряжения, подаваемого на электромагнитный привод. Установлено, что характер перемещения масс (моменты чередования зон покоя и перемещения) зависит от включения/выключения упругого элемента. Выявлено, что пиковое значение средней скорости системы зависит от частоты напряжения, подаваемого на электромагнитный привод, характер изменения средней скорости следующий: вначале плавное возрастание до максимального значения, затем плавное убывание практически до нуля, выпуклости обеих кривых направлены вниз.
Работа выполнена в рамках проекта РФФИ 15-51-12381.
Яцун С.Ф., Яцун А.С., Ворочаева Л.Ю. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ ДВУХМАССОВОГО ВИБРАЦИОННОГО МОБИЛЬНОГО РОБОТА // Фундаментальные исследования. 2015. № 12-4.
С. 729-734;






 и коэффициентом вязкого сопротивления µ1. Помимо этого между телами присутствует упругий ограничитель с недеформированной длиной
и коэффициентом вязкого сопротивления µ1. Помимо этого между телами присутствует упругий ограничитель с недеформированной длиной 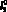 и жесткостью с3, причем с3 > > с1. Среда, действующая на массу 2 робота, представлена абсолютно твердым телом массой m3, их взаимодействие описывается моделью Кельвина ? Фойгта с параметрами с2, µ2 и длиной недеформированной пружины
и жесткостью с3, причем с3 > > с1. Среда, действующая на массу 2 робота, представлена абсолютно твердым телом массой m3, их взаимодействие описывается моделью Кельвина ? Фойгта с параметрами с2, µ2 и длиной недеформированной пружины 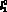 .
.
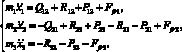 (1)
(1)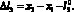 (2)
(2)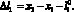 (3)
(3)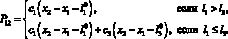 (4)
(4)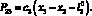 (5)
(5)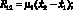
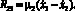 (6)
(6)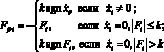 , (7)
, (7) (8)
(8)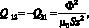 (9)
(9)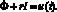 (10)
(10)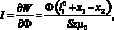 (11)
(11) (12)
(12)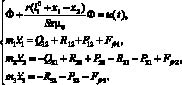 (13)
(13)




