Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Сухинов А.И. 1 Тимофеева Е.Ф. 2 Григорян Л.А. 2 Тебуева Ф.Б. 2 Никитина А.В. 3 Хачунц Д.С. 4

---

1 ФГБОУ ВПО «Донской государственный технический университет»

2 ФГАОУ ВПО «Северо-Кавказский федеральный университет

3 ГОУ ВО «Научно-исследовательский институт многопроцессорных вычислительных систем имени академика А.В. Каляева»,

4 ГОУ ВО «Научно-исследовательский институт многопроцессорных вычислительных систем имени академика А.В. Каляева»

Добыча нефти в большинстве случаев происходит при вытеснении ее в поровом пространстве продуктивного пласта водой или газом. Этот процесс применяется при естественных режимах эксплуатации и при искусственных методах поддержания пластового давления нагнетанием воды или газа. Задачи увеличения нефтеотдачи месторождений, имеющие важное практическое значение, приводят к необходимости массового решения задач фильтрации двухфазных несжимаемых жидкостей. Это, в свою очередь, требует при проектировании разработок нефтяных месторождений разрабатывать и применять параллельные алгоритмы, обеспечивающие высокую масштабируемость и возможность эффективного решения на многопроцессорных вычислительных системах. В статье рассматриваются вариант усовершенствованного попеременно-треугольного метода, учитывающий специфику постановок задач двухфазной фильтрации в естественных переменных «давление ? водонасыщенность», а также его параллельная реализация на системе с массовым параллелизмом – супервычислительной системе ЮФУ, установленной в Таганроге.

Статья в формате PDF

716 KB

моделирование задач двухфазной фильтрации

улучшенный итерационный попеременно-треугольный метод

параллельные алгоритмы

1. Бузало Н.С., Ермаченко П.А., Проценко Е.А., Ха чунц Д.С., Чистяков А.Е. Трехмерная математическая модель динамики жидкости и концентрации воздушных пузырьков в карусельном аэpотенке // Современные проблемы науки и образования. – 2015. – № 1. – С. 1789.

2. Гущин В.А., Матюшин П.В. Математическое моделирование и визуализация трансформации вихревой структуры течения около сферы при увеличении степени стратификации жидкости // Журнал вычислительной математики и математической физики. – 2011. – Т. 51, № 2. – С. 268–281.

3. Коновалов А.Н. Задачи фильтрации многофазной несжимаемой жидкости. – Новосибирск: Наука, 1988. – 166 с.

4. Коновалов А.Н. Метод скорейшего спуска с адаптивным попеременно-треугольным переобусловливателем // Дифференциальные уравнения. – 2004. – Т. 40, № 7. – С. 953.

5. Петров И.Б., Фаворская А.В., Санников А.В., Квасов И.Е. Сеточно-характеристический метод с использованием интерполяции высоких порядков на тетраэдральных иерархических сетках с кратным шагом по времени // Математическое моделирование. – 2013. – Т. 25, № 2. – С. 42–52.

6. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. – М.: Наука, 1978. – С. 592.

7. Сухинов А.И. Модифицированный попеременно-треугольный метод для задач теплопроводности и фильтрации // Вычислительные системы и алгоритмы. – 1984. – C. 52–59.

8. Сухинов А.И., Никитина А.В., Чистяков А.Е., Семенов И.С. Математическое моделирование условий формирования заморов в мелководных водоемах на многопроцессорной вычислительной системе // Вычислительные методы и программирование: новые вычислительные технологии. – 2013. – Т. 1, № 1. – С. 103–112.

9. Сухинов А.И., Хачунц Д.С., Чистяков А.Е. Математическая модель распространения примеси в приземном слое атмосферы и ее программная реализация на многопроцессорной вычислительной системе // Вестник Уфимского государственного авиационного технического университета. – 2015. – Т. 19, № 1. – С. 213–223.

10. Сухинов А.И., Чистяков А.Е. Адаптивный попеременно-треугольный метод для решения сеточных уравнений с несамосопряженным оператором // Математическое моделирование. – 2012. – Т. 24, № 1. – С. 3–20.

11. Сухинов А.И., Чистяков А.Е., Проценко Е.А. Математическое моделирование транспорта наносов в прибрежной зоне мелководных водоемов // Математическое моделирование. – 2013. – Т. 25, № 12. – С. 65–82.

12. Сухинов А.И., Чистяков А.Е., Тимофеева Е.Ф., Шишеня А.В. Математическая модель расчета прибрежных волновых процессов // Мат. моделирование. – 2012. – Т. 24, № 8. – С. 32–44.

13. Сухинов А.И., Чистяков А.Е., Фоменко Н.А. Методика построения разностных схем для задачи диффузии-конвекции-реакции, учитывающих степень заполненности контрольных ячеек // Известия Южного федерального университета. Технические науки. – 2013. – № 4 (141). – С. 87–98.

14. Сухинов А.И., Шишеня А.В. Повышение эффективности попеременно-треугольного метода на основе уточненных спектральных оценок // Математическое моделирование. – 2012. – Т. 24, № 11. – С. 10–22.

15. Четверушкин Б.Н., Морозов Д.Н, Трапезнико ва М.А., Чурбанова Н.Г., Шильников Е.В. Ободной схеме для решения задач фильтрации // Математическое моделирование. – 2010. – Т. 22, № 4. – C. 99–109.

Постановка начально-краевой задачи и разностная схема

Развитию вычислительных методов решения задач фильтрации многофазных жидкостей посвящены работы [3, 15], в том числе параллельному численному решению данного класса задач – публикации [7]. В случае плоско-параллельного характера фильтрации в пластах сравнительно небольшой мощности, уравнения, описывающие фильтрацию двухфазной несжимаемой жидкости в отсутствие капиллярных и гравитационных сил и при наличии источников и стоков, имеют вид [7]

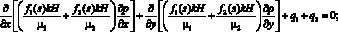(1)

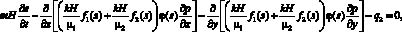(2)

где s = s(x, y) – водонасыщенность; p = s(x, y, t) – давление; f1(s), f2(s) – относительные фазовые проницаемости для нефти и воды соответственно; H – мощность пласта; m –пористость пласта; ?1, ?2 – вязкость нефти и воды соответственно; k(x, y) – проницаемость пласта; ?(s) – так называемая функция Баклея – Леверетта

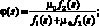
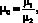(3)

с помощью которой может быть определена доля фазы воды в суммарном потоке. Функции q1 и q2, моделирующие работу скважин будут приведены при описании разностной схемы. Здесь мы отметим следующее: на эксплуатационных скважинах отбор фаз происходит пропорционально их подвижностям, а на нагнетательных – поток нефти равен нулю. Будем считать, что на скважинах задаются либо дебиты, либо забойные давления. В качестве функциональных зависимостей для задания f1(s), i = 1, 2 будем использовать полиномы третьего порядка

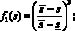
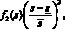(4)

а также

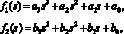(5)

где  – постоянные – так называемые предельные значения водонасыщенности, например 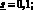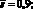ai, bi i = 0, 1, 2, 3 – постоянные коэффициенты. Разностная схема для данной задачи получена интегроинтерполяционным методом [13].

Усовершенствованный алгоритм модифицированного попеременно-треугольного метода

В настоящей статье рассматривается параллельное численное решение системы разностных уравнений усовершенствованным модифицированным попеременно-треугольным методом, имеющим высокую скорость сходимости в случае сильно неоднородных пластов и применения подробных пространственных сеток [1, 2, 5, 11, 12].

Решение системы (1), (2) сводится к решению задачи, которую можно представить в операторном виде:

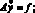
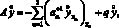x ? ?;

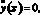x ? ?;

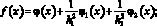
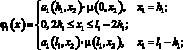
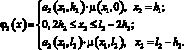
Схема итерационного двухслойного модифицированного попеременно-треугольного метода имеет вид [4, 6, 10, 14]:

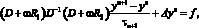
где

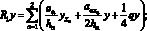
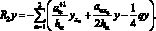
Параллельная реализация попеременно-треугольного метода и результаты численных экспериментов

Для решения задачи фильтрации двухфазной несжимаемой жидкости использован адаптивный МПТМ минимальных поправок. При параллельной реализации использованы методы декомпозиции сеточных областей для вычислительно трудоемких задач диффузии-конвекции, учитывающие архитектуру и параметры многопроцессорной вычислительной системы ЮФУ, в г. Таганроге. Пиковая производительность МВС составляет 18.8 TFlops. В качестве вычислительных узлов используется 128 однотипных 16-ядерных Blade-серверов HP ProLiant BL685c, каждый из которых оснащен четырьмя 4-ядерными процессорами AMD Opteron 8356 2.3 GHz и оперативной памятью в объеме 32ГБ.

Для параллельной реализации усовершенствованного МПТМ использованы методы декомпозиции области по одному направлению [8, 9]. Результаты использования многопроцессорных технологий для расчета полей течений приведены в таблице.

Получены теоретические оценки ускорения и эффективности параллельного алгоритма, зависящие от времени выполнения арифметической операции, времени передачи данных и латентности, согласующиеся с приведенными выше экспериментальными данными (таблица).

На рис. 1–4 представлены результаты численного моделирования фильтрации двухфазной несжимаемой жидкости. На рис. 1–2 приведена функция, описывающая распределение давления в начальный момент времени и через 750 суток после начала работы нагнетательных скважин.

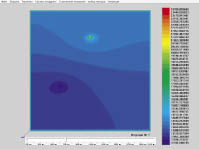
Рис. 1. Функция распределения давления в начальный момент времени

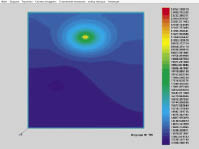
Рис. 2. Функция распределения давления через 750 суток

На рис. 3–4 приведена функция, описывающая распределение функции водонасыщенности в начальный момент времени и через 750 суток после начала работы нагнетательных скважин.

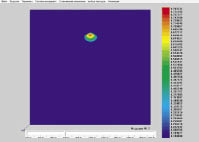
Рис. 3. Функция распределения водонасыщенности в начальный момент времени

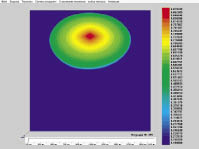
Рис. 4. Функция распределения водонасыщенности через 750 суток

Заключение

В статье для численного решения модельной задачи фильтрации двухфазной жидкости, описывающей процесс вытеснения нефти водой, для вычисления функции давления в пласте построен усовершенствованный модифицированный попеременно-треугольный метод, учитывающий специфику сеточных аппроксимаций задач такого типа – наличие функции источников, имеющей значительные величины в относительно небольшом числе узлов сетки, совпадающих с местоположением скважин. Построена и протестирована параллельная версия данного алгоритма на многопроцессорной системе ЮФУ в г. Таганроге, имеющая приемлемые показатели ускорения и эффективности для числа ядер при их изменении в диапазоне 4–256. Данный метод может найти применение при решении реальных задач проектирования разработок нефтяных месторождений в научно-исследовательских, проектных и технологических организациях нефтегазового профиля, эксплуатирующих относительно недорогие параллельные многоядерные системы с числом ядер до нескольких сотен.

Работа выполнена при частичной поддержке проектов Программы № 43 фундаментальных исследований Президиума РАН по стратегическим направлениям развития науки «Фундаментальные проблемы математического моде лирования».

Библиографическая ссылка