При решении задач математического моделирования процессов обработки металлов давлением (ОМД), направленных на совершенствование разрабатываемых технологических процессов, далеко не всегда можно ограничиться рассмотрением плоского случая. Большинство типов поковок требуют моделирования с использованием трех измерений. Несмотря на то, что многие математические методы, изначально ориентированные на два измерения, относительно легко переносятся на случай трех измерений, это не относится к важной сопутствующей проблеме – дискретизации пространства, необходимой для применения основного инструмента моделирования – метода конечных элементов (МКЭ). Основным способом деления пространства на элементарные объемы является разбиение на тетраэдры, которое по аналогии с двумерным разбиением области на треугольники принято называть триангуляцией. В настоящее время разработано большое количество программных пакетов моделирования, реализующих построение тетраэдральных сеток. В основном это дорогостоящие коммерческие пакеты, такие как ANSYS, NASTRAN, а в области моделирования пластических деформаций – DEFORM-3D, QForm-3D и другие. Тем не менее, количество алгоритмов и их реализаций для трехмерного случая значительно меньше, чем для двумерного, и работы в данном направлении по-прежнему актуальны.
Существующие методы трехмерной триангуляции по принципу работы в целом повторяют свои двумерные аналоги. Для относительно простых по форме областей могут применяться прямые методы на основе шаблонов и отображений, а для сложных областей используются итерационные методы на основе критерия Делоне и методы исчерпывания (другое название – «фронтальные методы») [1]. При решении задач моделирования пластического формоизменения триангуляции подвергаются объекты различной сложности: заготовки простейшей формы, поковки на разных стадиях деформации (в том числе с облоем), а также штамповочный инструмент. Сам процесс характеризуется постоянным изменением области моделирования и высокими значениями градиентов скоростей деформации и температур, что ведет к необходимости построения достаточно мелкой сетки с возможностью локального уплотнения, которая постоянно перестраивается при достижении элементами высокой степени искажения. Все это требует от алгоритма триангуляции универсальности и стабильности. В таких условиях возможно применение только итерационных методов. В основу работы авторов был положен алгоритм исчерпывания «от ребра», предложенный И.А. Щегловым [5], в который были внесены необходимые уточнения и корректировки, связанные с особенностями рассматриваемой предметной области.
Одной из таких особенностей является способ получения исходных данных. Для триангуляции нами использовались трехмерные модели, импортированные из САПР КОМПАС-3D встроенной прикладной библиотекой. Структура такой модели повторяет известный формат STL – это совокупность QT полигонов (треугольников) 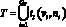 с заданными в них вершинами vi = (vi1, vi2, vi3) и нормалями
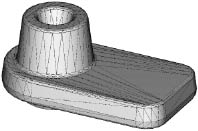
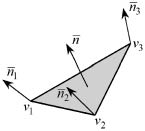
с заданными в них вершинами vi = (vi1, vi2, vi3) и нормалями 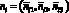 . На рис. 1, а показан пример импортированной модели, а на рис. 1, б приведена структура полигона. В терминах трехмерной триангуляции полигоны принято называть гранями.
. На рис. 1, а показан пример импортированной модели, а на рис. 1, б приведена структура полигона. В терминах трехмерной триангуляции полигоны принято называть гранями.
а б
Рис. 1. Модель, импортированная из КОМПАС-3D (а), и структура ее полигона (б)
Рассмотрим основные этапы предлагаемого алгоритма на блок-схеме (рис. 2).
Основным способом управления плотностью сетки является задание количества ее элементов. Но в программной реализации приходится использовать другую величину – среднюю длину ребра тетраэдра, которую принято называть шагом триангуляции (блок 2). Итерационные методы не позволяют точно спрогнозировать окончательное количество элементов, и для шага триангуляции только возможно рассчитать верхнее значение исходя из заданного количества элементов, объема области моделирования и предпочтительной формы элемента (правильный тетраэдр):
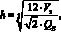
где h – шаг триангуляции; Vз – объем дискретизируемой модели; QE – заданное количество элементов.
Очевидно, что исходная поверхностная модель совершенно не подходит для построения качественной, адаптированной для последующего моделирования триангуляции. Поэтому она подвергается перестроению с учетом рассчитанного шага триангуляции, которое более подробно описано в работе [2]. В ходе адаптации полигоны объединяются в группы на основе плоскостей и участков кривых поверхностей, а затем переразбиваются с использованием метода двумерной триангуляции, описанного в [3]. Полученная таким образом полигональная поверхность становится исходным фронтом трехмерной триангуляции (блок 3). На основе множеств вершин и граней этой поверхности формируются множества узлов 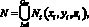 которые являются недублированными вершинами полигонов, и ребер
которые являются недублированными вершинами полигонов, и ребер 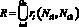 – недублированных сторон полигонов (QN и QR – количество уз лов и ребер). Такой способ хранения фронта (узлы, ребра, грани) является наиболее распространенным при построении трехмерной триангуляции.
– недублированных сторон полигонов (QN и QR – количество уз лов и ребер). Такой способ хранения фронта (узлы, ребра, грани) является наиболее распространенным при построении трехмерной триангуляции.
В основном цикле алгоритма (блоки с 4 по 14) производится последовательное исключение тетраэдральных элементов из области, ограниченной фронтом, вплоть до ее полного исчерпания. Построение начинается с выбора наиболее сложного участка фронта (блок 4). С этой целью в каждом ребре r ? R фронта производится расчет сложности Cr:
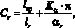
где lср – средняя длина ребер фронта; lr – длина ребра r (рис. 3); K? = 3 – коэффициент значимости угловой составляющей сложности; ?r – двугранный угол между треугольниками tm, tn ? T, образующими данное ребро. Согласно этой формуле большую сложность имеют ребра с малыми длиной и двугранным углом.
Для учета размеров граней и ребер выбранного участка фронта, а также возможности уплотнения сетки рассчитывается локальный шаг триангуляции (блок 5):
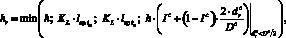
где KL = 1,3 – коэффициент максимального удлинения стороны элемента, позволяющий получать элементы с незначительным искажением; 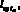
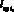 – средние длины сторон треугольников фронта tm, tn, образующих ребро; Ic – интенсивность сгущения сетки (0,2 ? Ic < 1); Dc – диаметр области сгущения;
– средние длины сторон треугольников фронта tm, tn, образующих ребро; Ic – интенсивность сгущения сетки (0,2 ? Ic < 1); Dc – диаметр области сгущения; 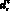 – расстояние от центра ребра до точки сгущения. Последний компонент рассматривается только при вхождении ребра r в область сгущения. Применение локального шага триангуляции, рассчитанного в текущем месте построения, вместо постоянного глобального шага, позволяет формировать сетки со сгущениями в местах со сложной формой (закругления, облойная канавка и т.д.) и участках области, где присутствуют высокие градиенты интенсивностей скоростей деформации.
– расстояние от центра ребра до точки сгущения. Последний компонент рассматривается только при вхождении ребра r в область сгущения. Применение локального шага триангуляции, рассчитанного в текущем месте построения, вместо постоянного глобального шага, позволяет формировать сетки со сгущениями в местах со сложной формой (закругления, облойная канавка и т.д.) и участках области, где присутствуют высокие градиенты интенсивностей скоростей деформации.
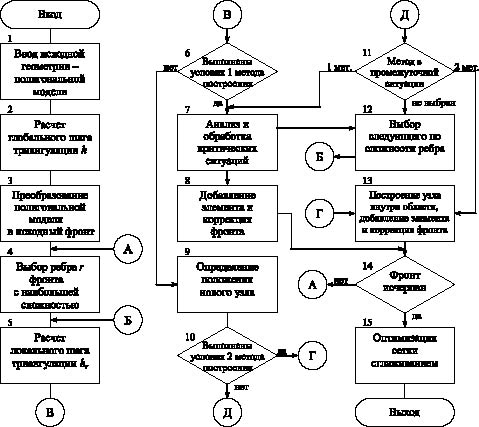
Рис. 2. Блок-схема алгоритма трехмерной триангуляции методом исчерпывания
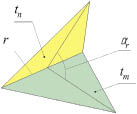
Рис. 3. Участок фронта с ребром r
Далее производится выбор метода построения тетраэдра на выбранном по сложности ребра фрагменте фронта (блоки 6, 10, 11). Рассматриваются два возможных варианта:
1) тетраэдр формируется без добавления нового узла путем соединения третьих точек граней, образующих ребро;
2) тетраэдр формируется путем создания нового узла внутри фронта и соединения его ребрами с меньшей из граней выбранного ребра.
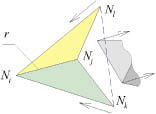
Рассмотрим подробнее процесс выбора метода построения. Приоритет созданию тетраэдра без образования нового узла (рис. 4, а) отдается в следующих случаях (блок 6):
а) двугранный угол имеет значение меньше, чем в правильном тетраэдре: ?r < ?пр = 70°53?;
б) значение двугранного угла находится в интервале 70°53? < ?r < 100°, и длина нового ребра (Nk, Nl) не превосходит hr;
в) ребро (Nk, Nl) уже существует в результате предыдущих построений.
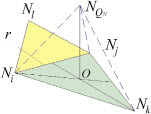
Формирование тетраэдра с новым узлом 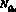 в качестве вершины происходит в обязательном порядке, если двугранный угол имеет большое значение: ?r > 120° (рис. 4, в) (блок 10). Во всех остальных случаях выбор одного из двух методов осуществляется на основе оценки качества получаемых тетраэдров, которое рассчитывается как отношение длин самого короткого и самого длинного ребер возможного тетраэдра (блок 11). Практика триангуляции моделей объектов ОМД показала, что первый метод используется в 80–85 % процентах тетраэдров, а второй – в оставшихся 15–20 %.
в качестве вершины происходит в обязательном порядке, если двугранный угол имеет большое значение: ?r > 120° (рис. 4, в) (блок 10). Во всех остальных случаях выбор одного из двух методов осуществляется на основе оценки качества получаемых тетраэдров, которое рассчитывается как отношение длин самого короткого и самого длинного ребер возможного тетраэдра (блок 11). Практика триангуляции моделей объектов ОМД показала, что первый метод используется в 80–85 % процентах тетраэдров, а второй – в оставшихся 15–20 %.
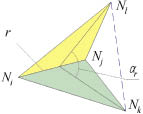
а б
в г
д
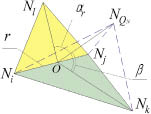
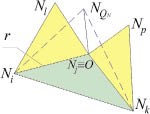
Рис. 4. Создание тетраэдра без нового узла (а, б) и с образованием нового узла (в, г, д)
Применение каждого из методов имеет свои особенности. Добавлению элемента в триангуляцию первым методом предшествует проверка критических ситуаций – ребра и грани фронта не должны пересекать вновь создаваемый тетраэдр. Также необходимо заранее прогнозировать появление тетраэдров и граней фронта с «плохой» узкой формой. Для устранения данной проблемы производится анализ близлежащих объектов фронта и внесение изменений во фронт и триангуляцию до построения тетраэдра (блок 7) путем перемещения узлов по схеме, показанной на рис. 4, б. Порядок действий в ходе добавления тетраэдра первым методом (блок 8) во многом определяется наличием или отсутствием во фронте ребра (Nk, Nl) и боковых граней (Ni, Nk, Nl), (Nj, Nk, Nl). При отсутствии ребра и граней (около 65 % элементов) в триангуляцию добавляется элемент с узлами Ni, Nj, Nk, Nl, а во фронт вставляются ребро (Nk, Nl) и грани (Ni, Nk, Nl), (Nj, Nk, Nl). В очень редко встречающейся ситуации отсутствия боковых граней и существования ребра (Nk, Nl), помимо описанного выполняется клонирование ребра (Nk, Nl), т.к. в нем необходимо знать уже два или более двугранных угла. Если существуют ребро и обе боковые грани, то производится добавление элемента, а текущий фрагмент фронта с узлами Ni, Nj, Nk, Nl, их гранями и ребрами удаляется (0,1 % элементов). В случае наличия ребра и одной боковой грани, например (Ni, Nk, Nl), следует добавить элемент в триангуляцию, вставить во фронт грань (Nj, Nk, Nl), удалить узел Ni и примыкающие к нему ребра и грани (16–19 % случаев).
В ходе добавления тетраэдра вторым методом (блок 13) во фронт вставляется новый узел, положение которого зависит от величины двугранных углов ребер опорной грани (Ni, Nj, Nk). Если все углы больше 2??пр, то он строится на перпендикуляре к центру масс опорной грани (рис. 4, в). Если угол в ребре r меньше 2??пр – на перпендикуляре к ребру r с углом ? = ?r/2 к грани от точки O, полученной усреднением Ni, Nj и проекций узлов Nk, Nl на r (рис. 4, г). Если два угла меньше 2??пр, узел строится на прямой, образованной пересечением биссекторных плоскостей ребер этих углов (рис. 4, д). Во всех случаях позиция узла подбирается так, чтобы средняя длина новых ребер была равна hr. Помимо нового узла во фронт добавляются три примыкающих к нему ребра и три грани, а опорная грань удаляется (блок 13). В ряде случаев не удается сформировать корректный тетраэдр ни одним из способов, тогда в качестве текущего берется следующее по сложности ребро (блок 12).
После завершения заполнения элементами области триангуляции производится оптимизация полученной сетки итерационным сглаживанием – каждый внутренний узел переносится в точку центра масс системы тетраэдров, содержащих данный узел (блок 17). Процедура сглаживания продолжается до тех пор, пока невязка перемещения узлов не станет меньше 0,01 мм. Как правило, для этого достаточно нескольких десятков итераций. На рис. 5 представлены результаты работы описанного алгоритма на примере двух поковок.

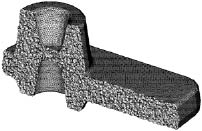
Рис. 5. Примеры триангуляции поковок
Заключение
Применение описанного алгоритма для триангуляции моделей типичных заготовок и поковок показало его способность формировать трехмерные сетки из тетраэдров, пригодные для моделирования пластической деформации методом конечных элементов. В качестве недостатка предложенного алгоритма можно назвать его последовательный характер, что усложняет распараллеливание процесса и интенсификацию расчетов на многоядерных процессорах и кластерах. Тем не менее работы в этом направлении ведутся, один из вариантов решения данной проблемы описан в работе [4].
Библиографическая ссылка
Покрас И.Б., Ахмедзянов Э.Р. АЛГОРИТМ ТРЕХМЕРНОЙ ТРИАНГУЛЯЦИИ В ЗАДАЧАХ МОДЕЛИРОВАНИЯ ПЛАСТИЧЕСКОГО ФОРМОИЗМЕНЕНИЯ // Фундаментальные исследования. 2015. № 12-3. С. 511-516;URL: https://fundamental-research.ru/ru/article/view?id=39571 (дата обращения: 12.03.2026).



