Метод вращающегося мембранного диска (ВМД) обладает рядом уникальных особенностей, это равнодоступность поверхности мембраны и постоянство толщины диффузионного слоя. Основой для создания метода ВМД послужила теория В.Г. Левича [7], согласно которой течение раствора под дисковым электродом имеет вид логарифмических спиралей, что обеспечивает равнодоступность поверхности вращающегося дискового электрода, а толщина диффузионного слоя ?dif зависит лишь от угловой скорости вращения ? дискового электрода: 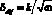 , где k постоянная, зависящая от коэффициента диффузии и кинематической вязкости.
, где k постоянная, зависящая от коэффициента диффузии и кинематической вязкости.
Теория Левича применима для вращающегося мембранного диска при допредельных токовых режимах, из-за чего он широко используется при изучении мембранных систем [2, 3]. В работах [1, 8] была предложена экспериментальная электрохимическая ячейка с ВМД с горизонтально расположенной катионообменной мембраной. Эта установка позволяет одновременно определять общие и парциальные ВАХ, ионные потоки и зависимость эффективных чисел переноса ионов электролита от угловой скорости вращения мембранного диска [8]. В работах [4, 5] теоретически была проверена равнодоступность поверхности мембранного диска в этой установке, но без учета электроконвекции, возникающей при запредельных токовых режимах.
Данная статья является продолжением работы [6], в которой была приведена математическая модель переноса ионов соли в вертикально стоящей цилиндрической ячейке с вращающейся вокруг центральной оси дисковой катионообменной мембраной при запредельных токовых режимах, с учетом электроконвекции, что приводит к существенному изменению гидродинамики. На основе этой модели в данной работе изучается зависимость толщины диффузионного слоя от угловой скорости.
Постановка задачи. Математическая модель и некоторые свойства процесса переноса ионов соли достаточно подробно изложены в [6]. В связи с этим здесь ограничимся кратким изложением модели, уделив основное внимание ее исследованию.
Используя осевую симметрию модели, представим область решения в виде половины сечения цилиндрической области (рис. 1). Следует иметь в виду, что половина сечения цилиндрической области вращается вокруг оси симметрии 2, причем:
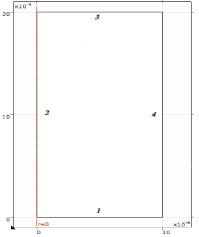
Рис. 1. Половина сечения цилиндрической области и ее границы
Граница 1 – глубина раствора, которая моделирует бесконечно удаленную от катионообменной мембраны часть, где выполняется условие электронейтральности, концентрация раствора постоянная (C0) и концентрации катионов и анионов считаются постоянными: Ci,0 = C0, i = 1, 2. Граница 1 является открытой границей (входом) для раствора, и для скорости ставится условие отсутствия нормального напряжения 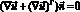 , давление при этом считается равным нулю. Кроме того, граница 1 считается также анодом, причем эквипотенциальной поверхностью, с ? = 0.
, давление при этом считается равным нулю. Кроме того, граница 1 считается также анодом, причем эквипотенциальной поверхностью, с ? = 0.
Граница 3 соответствует вращающейся идеально селективной катионообменной мембране, поэтому она считается выходом для катионов, концентрация которых постоянна и равна емкости мембраны: C1,0 = Ckm. Для анионов используется условие непроницаемости (отсутствия потока): 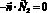 . Поверхность катионообменной мембраны считается эквипотенциальной: ? = d?. Для радиальной скорости используется условие: v = ?r.
. Поверхность катионообменной мембраны считается эквипотенциальной: ? = d?. Для радиальной скорости используется условие: v = ?r.
Граница 4 – открытая граница (выход) для раствора. На ней для ионов ставится условие выноса конвективным потоком 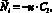 i = 1, 2. Для потенциала используется условие непроницаемости:
i = 1, 2. Для потенциала используется условие непроницаемости: 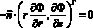 . Граница 4 считается выходом и для скорости ставится такое же граничное условие, как и для границы 1.
. Граница 4 считается выходом и для скорости ставится такое же граничное условие, как и для границы 1.
Скорость течения раствора на входе и выходе определяется по ходу решения.
Будем считать, что вначале ячейка заполнена раствором бинарной соли (например, NaCl) с равномерно распределенной концентрацией C0.
Для моделирования переноса ионов соли и течения раствора используется система уравнений Нернста – Планка и Пуассона и Навье – Стокса Векторная запись этой системы для бинарного электролита при отсутствии химических реакций, в декартовой системе координат, имеет вид
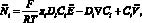 i = 1, 2; (1)
i = 1, 2; (1)
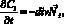 i = 1, 2; (2)
i = 1, 2; (2)
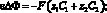 (3)
(3)
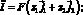 (4)
(4)
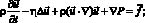 (5)
(5)
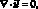 (6)
(6)
где ? – градиент; ? – оператор Лапласа; 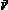 – скорость течения раствора;
– скорость течения раствора; 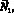
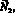 C1, C2 – потоки и концентрации катионов и анионов в растворе соответственно; z1, z2 – зарядовые числа катионов и анионов;
C1, C2 – потоки и концентрации катионов и анионов в растворе соответственно; z1, z2 – зарядовые числа катионов и анионов; 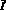 – плотность тока; D1, D2 – коэффициенты диффузии катионов и анионов соответственно; ? – потенциал электрического поля;
– плотность тока; D1, D2 – коэффициенты диффузии катионов и анионов соответственно; ? – потенциал электрического поля; 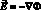 – напряженность электрического поля; ? – диэлектрическая проницаемость электролита; F – постоянная Фарадея; R – газовая постоянная; T – абсолютная температура; t – время; ? – коэффициенты кинематической вязкости; u – скорость; ? – плотность; ? – динамическая вязкость; P – давление;
– напряженность электрического поля; ? – диэлектрическая проницаемость электролита; F – постоянная Фарадея; R – газовая постоянная; T – абсолютная температура; t – время; ? – коэффициенты кинематической вязкости; u – скорость; ? – плотность; ? – динамическая вязкость; P – давление; 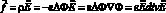 – объемная электрическая сила.
– объемная электрическая сила.
Замечание 1. Поскольку под мембраной образуется запирающий слой обессоленного раствора, влияние гравитационной конвекции несущественно.
Для численного решения краевой задачи используется метод конечных элементов в цилиндрической системе координат с неравномерной сеткой.
Анализ численных результатов
Рассмотрим некоторые результаты моделирования переноса ионов соли в электрохимической ячейке с вращающимся мембранным диском.
1. Методика расчета толщины диффузионного слоя
На рис. 2 приведены сечения линий тока раствора вблизи катионообменной мембраны. В центре мембранного диска образуется электроконвективный вихрь. Раствор обтекает этот вихрь, и перед ним образуется застойная зона. С увеличением угловой скорости при заданном падении потенциала размеры электроконвективного вихря уменьшаются, и при некотором значении угловой скорости электроконвективный вихрь исчезает. Вдали от оси вращения линии тока раствора близки к логарифмическим спиралям [6].
На рис. 3 приведен график концентрации катионов вблизи катионообменной мембраны.
Значения концентрации практически линейно уменьшаются в диффузионном слое от постоянного значения до минимального постоянного значения, а затем снова увеличиваются в узкой области вблизи катионообменной мембраны (часть квазиравновесного погранслоя), удовлетворяя граничному условию. В дальнейших рассуждениях этот погранслой, обусловленный граничным условием на концентрацию катионов на поверхности катионообменной мембраны, имеющий привнесенный характер и малые размеры, не участвует.
Как следует из рис. 3, вдали от центра диска толщина диффузионного слоя практически постоянна. Внешняя граница диффузионного слоя определяется по точке, в которой концентрация меняется на какой-то фиксированный процент (в работе на 5 %) от своего начального значения (рис. 4). Далее рассчитывается толщина диффузионного слоя ?dif.
2. Зависимость толщины диффузионного слоя от угловой скорости
Из формулы Левича [7] следует, что величина 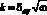 – постоянная. Ниже в таблице приведены зависимость толщины диффузионного слоя от угловой скорости и значение
– постоянная. Ниже в таблице приведены зависимость толщины диффузионного слоя от угловой скорости и значение 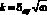 , рассчитанные в рамках данной модели.
, рассчитанные в рамках данной модели.
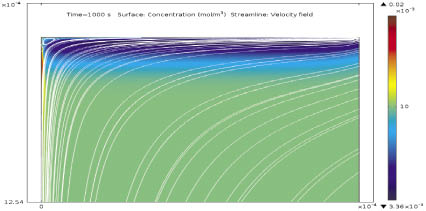
Рис. 2. Линии тока раствора вблизи мембранного диска жидкости в момент времени t = 1000 с при угловой скорости 30 оборотов в минуту и разности потенциала d? = 0,3 В
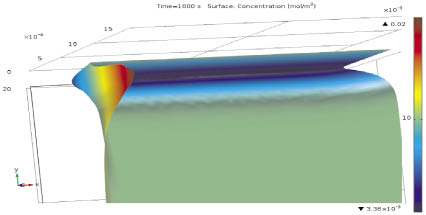
Рис. 3. График концентрации катионов в момент времени t = 1000 с при угловой скорости 30 оборотов в минуту и разности потенциала d? = 0,3 В
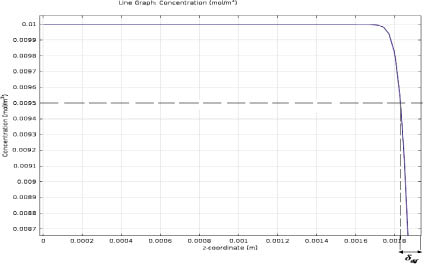
Рис. 4. Схема определения толщины диффузионного слоя
Зависимость толщины диффузионного слоя ?dif (мм) от угловой скорости ? (рад/с)
|
?, рад/с |
0 |
? |
2? |
3? |
4? |
5? |
6? |
7? |
8? |
9? |
10? |
|
?dif, мм |
0,796 |
0,165 |
0,097 |
0,071 |
0,056 |
0,046 |
0,039 |
0,033 |
0,028 |
0,024 |
0,0182 |
|
k |
0,0 |
0,29 |
0,24 |
0,218 |
0,199 |
0,182 |
0,169 |
0,155 |
0,14 |
0,128 |
0,102 |
Как видно из таблицы, значение k нельзя считать постоянным и следует ввести поправку в формулу Левича, учитывающую влияние электроконвекции.
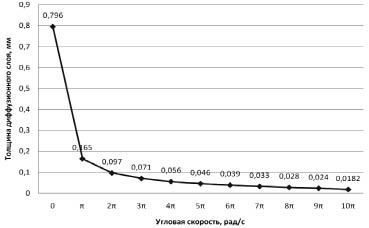
Рис. 5. График зависимости толщины диффузионного слоя в мм от угловой скорости в рад/с
Заключение
В работе проведен численный анализ краевой задачи для системы уравнений Нернста – Планка – Пуассона и Навье – Стокса, моделирующей перенос ионов соли в цилиндрической ячейке с вращающимся катионообменным мембранным диском. Рассчитана зависимость толщины диффузионного слоя от угловой скорости. Показано, что следует ввести поправку в формулу Левича, учитывающую влияние электроконвекции.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 13-08-00464 а и № 13-08-01460-а.
Библиографическая ссылка
Коваленко А.В., Уртенов М.Х., Казаковцева Е.В., Бостанов Р.А., Лайпанова З.М. ПЕРЕНОС ИОНОВ СОЛИ В ЭЛЕКТРОХИМИЧЕСКОЙ ЯЧЕЙКЕ С ВРАЩАЮЩИМСЯ МЕМБРАННЫМ ДИСКОМ С УЧЕТОМ ЭЛЕКТРОКОНВЕКЦИИ. ЗАВИСИМОСТЬ ТОЛЩИНЫ ДИФФУЗИОННОГО СЛОЯ ОТ УГЛОВОЙ СКОРОСТИ // Фундаментальные исследования. 2015. № 12-3. С. 463-467;URL: https://fundamental-research.ru/ru/article/view?id=39562 (дата обращения: 21.02.2026).
DOI: https://doi.org/10.17513/fr.39562



