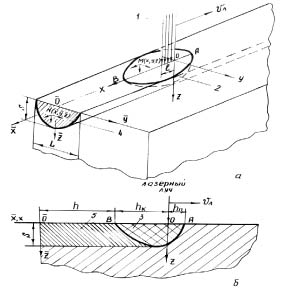
Рассматриваемый процесс является квазистационарным. Это означает, что температура любой точки, жестко связанной с источником, не меняется во времени, т.е. в подвижной системе координат, связанной с источником тепла, температура точки М(x, y, z) не меняется со временем. Вместе с тем температура фиксированных точек 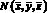 , жестко связанных с подвижным телом, меняется во времени. В связи с движением источника имеет место температурная анизотропия, т.е. неодинаковость теплового влияния источника в различных направлениях.
, жестко связанных с подвижным телом, меняется во времени. В связи с движением источника имеет место температурная анизотропия, т.е. неодинаковость теплового влияния источника в различных направлениях.
Для определения температурного поля, т.е. функции распределения температуры Т(X, Y) в точках с координатами (x, y) в подвижной системе координат в жидкой и твердой фазах процесс разобьем на три стадии: 1 – материал нагревается до точки плавления (твердая фаза); 2 – материал находится в жидкой фазе; 3 – материал находится в стадии затвердевания.
Рассмотрим квазистационарный процесс, при котором материал прогревается до температуры меньше температуры плавления.
Для начальной стадии нагрева принимается математическая модель, состоящая в том, что функция Т(X, Y) удовлетворяет уравнению [4]:
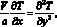 (1)
(1)
где V – скорость движения лазерного луча (м/с); а = l/сg – коэффициент температуропроводности (м2/с); l – коэффициент теплопроводности (Вт/м?К); с – удельная теплоемкость (Дж/кг?К); g – плотность (кг/м3).
Граничные условия для уравнения (1) имеют вид
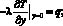 (2)
(2)
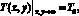 (3)
(3)
где q – плотность потока (Вт/м2).
Второе граничное условие связано с неограниченностью тела и сводится к предположению о том, что далекие от источника тепла точки тела имеют начальную температуру Т0.
Полагая, что температурное поле обладает автомодельностью, для решения уравнения (1) с граничными условиями (2) и (3) введем переменную x
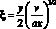 (4)
(4)
и новую функцию
q(x) = Т – Т0. (5)
Уравнение (1) в новых переменных примет вид
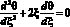 (6)
(6)
или 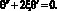 (7)
(7)
Граничное условие (2) с учетом, что при Y = 0, x = 0 (4), получим
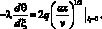 (8)
(8)
С учетом (5) граничное условие (3) примет вид
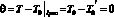
или 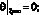
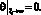 (9)
(9)
Решение уравнения (1) при использовании новых переменной x и функции q(x) имеет вид
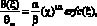 (10)
(10)
где 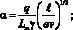
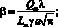 Lm – теплота плавления (Дж/кг); Qm = Tm – T0 (К); Tm – температура плавления (К); T0 – начальная температура (К);
Lm – теплота плавления (Дж/кг); Qm = Tm – T0 (К); Tm – температура плавления (К); T0 – начальная температура (К); 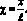
Предполагаем наличие в теле изотермической поверхности, точки которой имеют температуру Т = Тm – температуру плавления. Ясно, что внутри этой изотермической поверхности тело будет находиться в жидкой фазе и иметь свои теплофизические характеристики а1, l1 и т.д.
Указанная изотермическая поверхность (Т = Тm) соответствует значению функции q(x) = qm = Тm – T0. Поскольку q(x) является функцией одной переменной x, то существует ее значение x = xs, при котором q(xs) = qm. Значение переменного x = xs соответствует тем значениям переменных Х и Y по формуле (4), при которых точка с координатами (Х, Y) принадлежит изотермической поверхности – Т = Тm.
Решение задачи (1) с граничными условиями (2) и (3) (с использованием новых переменных и функции) имеет вид
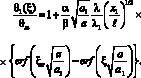 (11)
(11)
Полученное выражение (11) позволяет определить характер распределения температуры внутри ванны расплава.
Вне ванны расплава, т.е. вне изотермической поверхности T = Tm, что соответствует значению переменной x = xs, распределение температурного поля будет удовлетворять уравнению (7), в котором: q(x) – температура точек тела, расположенных вне ванны расплава; x – переменная, которая определяется из (4).
Первое граничное условие состоит в том, что распределение температуры в точках фазового перехода постоянно Т = Тm, т.е. при x = xs q(xs) = Тm – Т0 = qm.
Второе граничное условие выражает тот факт, что в достаточно удаленных точках массивного тела температура равна начальной температуре Т = Т0. Из этого следует, что при x = ? q(?) = Т0 – Т0 = 0.
Таким образом, граничные условия примут вид
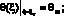
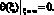 (12)
(12)
В результате задача нахождения распределения температуры в твердой фазе свелась к нахождению решения уравнения (7), удовлетворяющего граничным условиям (12).
Общее решение уравнения (7) имеет вид
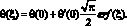 (13)
(13)
Это позволяет получить решение (7) и (12)
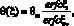 (14)
(14)
которое определяет распределение температурного поля в твердой фазе вне ванны расплава.
Используя уравнение теплового баланса на границе фазового перехода, то есть значением переменной x = xs и уравнения (11) и (14), можно получить трансцендентное уравнение, связывающее при фиксированном значении х = const переменную
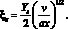 (15)
(15)
Это уравнение имеет вид
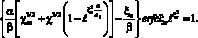 (16)
(16)
Глубина ванны расплава в плоскости х = const (в силу предположения о симметрии относительно оси ОХ) определяется из выражения
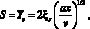 (17)
(17)
где xs является решением уравнения (16).
Результаты расчета параметров, характеризующих форму ванны расплава технически чистого титана (ВТ1-0) при подвижном лазерном источнике для постоянной q = 3,2?108 Вт/м2 и Vл, изменяющейся в диапазоне (0,00166–0,015) м/с, а также для Vл = 0,0083 м/с и изменяющейся в диапазоне (1,68?108–8,1?108) Вт/м2 q приведены на рис. 2 и 3.
Увеличение скорости лазерного источника приводит к уменьшению глубины ванны расплава и длины зоны плавления. На рис. 2 видно, что при увеличении скорости движения лазерного излучения фронт плавления (координаты точек начала плавления (hn)) и кристаллизации (координаты точек кристаллизации (hk)) смещается в противоположную сторону относительно направления движения лазерного луча.
Результаты влияния плотности мощности лазерного излучения на характеристики формы ванны расплава титана при подвижном тепловом источнике приведены на рис. 3.
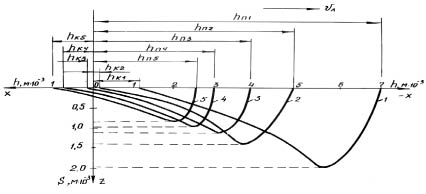
Рис. 2. Формы ванн расплава при q = 3,2?108 Вт/м2 в плоскости Y = 0 при различных скоростях лазерного излучения: 0,0016 (1); 0,005 (2); 0,0083 (3); 0,0116 (4) и 0,015 (5) м/с
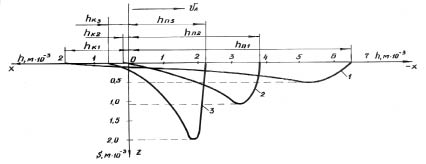
Рис. 3. Формы ванн расплава при Vл = 0,0083 м/с в плоскости сечения Y = 0 при различных плотностях мощности лазерного излучения: 1,68?108 (1); 3,2?108 (2) и 8,1?108 (3) Вт/м2
Изменение плотности мощности лазерного луча в процессе исследований осуществлялось путем варьирования диаметра пучка лазера за счет изменения фокусного расстояния при неизменной мощности лазера, которая составляла 160 Вт. Полученные результаты показывают, что увеличение плотности мощности лазерного излучения от q = 1,68?108 до q = 8,1?108 Вт/м2 при постоянной скорости перемещения лазерного источника приводит к росту глубины ванны расплава и соответствующему уменьшению площади зоны плавления.
Экспериментальные исследования выполнены при тех численных значениях режимных параметров, которые были использованы в расчетах по определению характеристик ванн расплава.
Металлографическим путем определялась максимальная глубина ванны расплава, полученная при различных режимных параметрах лазерного излучения.
Принятые в экспериментальных исследованиях численные значения скоростей перемещения лазерного излучения при неизменной плотности мощности теплового потока (q = 3,2?108 Вт/м2) обеспечивают следующие величины максимальных глубин ванн расплава: 6,0?10–5 м; 5,0?10–5 м; 3,7?10–5 м; 2,9?10–5 м и 2,0?10–5 м для указанных на рис. 2 значений Vл соответственно. Плотности мощности лазерного излучения при неизменной скорости перемещения лазерного луча (Vл = 0,0083 м/с) формируют ванны расплава со следующими максимальными глубинами: q = 1,6?108 Вт/м2 – 2,0?10–5 м, q = 3,2?108 Вт/м2 – 3,7?10–5 м и q = 8,1?108 Вт/м2 – 6,0?10–5 м.
Сопоставление расчетных и экспериментальных характеристик ванн расплава указывает на их качественное соответствие. Некоторые количественные расхождения в расчетах и экспериментальных значениях глубин зон расплава связаны, прежде всего, с неопределенностью коэффициента отражения, представляющего собой отношение интенсивностей отраженной и падающей волн.
Таким образом, проведенный анализ по определению температурных полей и параметров ванны расплава титана при непрерывном лазерном излучении может быть использован для определения физических характеристик процесса ЛТО. Он позволяет путем целенаправленного воздействия режимными параметрами лазерного излучения прогнозировать основные характеристики получаемого упрочненного слоя и, прежде всего, глубину ванны расплава.
Рецензенты:
Амосов А.П., д.ф.-м.н., профессор, зав. кафедрой металловедения, порошковой металлургии, наноматериалов, Самарский государственный технический университет, г. Самара;
Самборук А.Р., д.т.н., зав. опытно-промышленной базой «Петра Дубрава», Самарский государственный технический университет, г. Самара.
Муратов В.С., Морозова Е.А. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРНЫХ ПОЛЕЙ И ПАРАМЕТРОВ ВАННЫ РАСПЛАВА НА ПОВЕРХНОСТИ ТИТАНА ПРИ НЕПРЕРЫВНОЙ ЛАЗЕРНОЙ ОБРАБОТКЕ // Фундаментальные исследования. 2015. № 11-4.
С. 719-723;




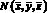 , жестко связанных с подвижным телом, меняется во времени. В связи с движением источника имеет место температурная анизотропия, т.е. неодинаковость теплового влияния источника в различных направлениях.
, жестко связанных с подвижным телом, меняется во времени. В связи с движением источника имеет место температурная анизотропия, т.е. неодинаковость теплового влияния источника в различных направлениях.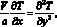 (1)
(1)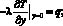 (2)
(2)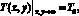 (3)
(3)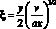 (4)
(4)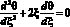 (6)
(6)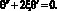 (7)
(7) (8)
(8)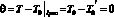
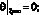
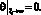 (9)
(9)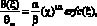 (10)
(10)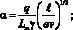
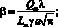 Lm – теплота плавления (Дж/кг); Qm = Tm – T0 (К); Tm – температура плавления (К); T0 – начальная температура (К);
Lm – теплота плавления (Дж/кг); Qm = Tm – T0 (К); Tm – температура плавления (К); T0 – начальная температура (К); 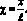
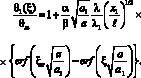 (11)
(11)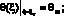
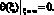 (12)
(12)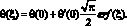 (13)
(13)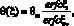 (14)
(14)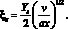 (15)
(15)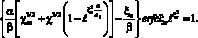 (16)
(16)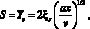 (17)
(17)
