Нечеткое управление в настоящее время является одной из перспективных интеллектуальных технологий, позволяющих создавать высококачественные системы управления [1, 7]. Нечеткий регулятор (НР) либо сам формирует управляющие воздействия, поступающие на вход объекта, либо сигналы нечеткого блока вывода управляют параметрами регулятора традиционной системы управления [5, 7]. Например, в работах [2, 3] рассматривается система, в которой производится автоматическая динамическая коррекция параметров ПИД-регулятора сигналами, подаваемыми с блоков нечеткого логического вывода, аппроксимирующих нелинейные операторы, полученные с использованием принципа максимума. К недостаткам данного подхода относится то, что найти оптимальное управление удается только в том случае, если имеется точная модель объекта управления. Причем открытым остается вопрос о том, каким образом аппроксимировать полученный оптимальный закон нечеткой системой, а также отсутствие каких-либо гарантий качества синтезированной системы управления при изменении параметров объекта.
Устранение указанных недостатков при решении задачи управления динамическим объектом в условиях неопределенности может быть достигнуто при сочетании классических методов теории управления и методов нечеткого управления [1]. Нечеткие системы обладают важным свойством аппроксимировать любую нелинейную функцию с любой точностью. Это дает возможность использовать для построения нечеткого регулятора аналитические выражения для управляющих воздействий, полученные аппроксимацией различных нелинейностей методами, известными из традиционной теории автоматического управления. При этом реализуется гибридная технология, сочетающая как качественные принципы синтеза нечетких систем, так и количественные принципы теории управления [7]. Несмотря на эффективность данного подхода к синтезу нечеткого регулятора, рекомендации по выбору рациональной структуры нечеткого регулятора для коррекции параметров настройки регулятора основного контура системы отсутствуют. Приведенные в [6] примеры показывают, что форма характеристик нечеткого регулятора (контроллера) во многом зависит от базы правил и функций принадлежности (ФП) входных и выходной переменной. Поэтому для раскрытия сущности предложенного метода синтеза целесообразно привести из [6] некоторые результаты анализа влияния ФП и базы правил на характеристики нечеткого регулятора.
Анализ влияния функции принадлежности на характеристики нечеткого регулятора и особенности метода параметрического синтеза
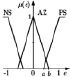
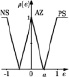
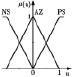
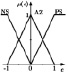
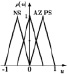
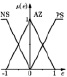
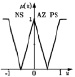
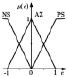
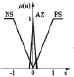
Для некоторых задач управления могут быть использованы простые, распространенные треугольные функции принадлежности со следующими лингвистическими термами, например: NL – большое отрицательное, PL – большое положительное, NM – среднее отрицательное, AZ – ноль, PM – среднее положительное, NS – малое отрицательное, PS – малое положительное. В [6] приведены примеры нечеткой системы, в которых треугольные функции принадлежности пересекаются, как для входных переменных, так и для выходной переменной. В качестве этих переменных в большинстве работ используются значения сигнала ошибки εK, скорости ее изменения dεK/dt и управляющего воздействия uk в k-й момент времени tk (k = 0,1,2). Входные и выходные значения нормализованы на отрезке [–1; 1]. Рассмотрим для установившегося режима только три лингвистических терма: NS (малое отрицательное), AZ (ноль), PS (малое положительное). Тогда правила формирования выходного сигнала нечеткого регулятора с функциями принадлежности, представленными в таблице (первая строка), можно записать в следующем виде:
П I: ЕСЛИ εK = NS, ТО uk = NS;
П II: ЕСЛИ εK = АZ, ТО uk = АZ;
П III: ЕСЛИ εK = PS, ТО uk = PS.
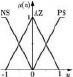
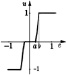
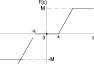
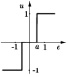
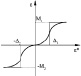
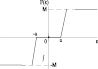
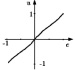
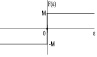
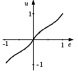
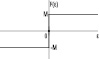
Из-за различных оснований функции принадлежности характеристика НР приблизительно кусочно-линейна и имеет три отчетливых уровня. Функция принадлежности входного сигнала εK имеет два пересечения (перекрытия), которые точно соответствуют диапазонам положительных наклонов кривой. Причиной тому является то, что два правила в этих диапазонах одновременно активны. В случае без пересечений во входной функции получается характеристика трехпозиционного (с тремя состояниями) регулятора, как показано на рисунке в таблице (вторая строка). В этом случае одно правило активно, поэтому на выходе появляются только три четких значения: –1, 0, +1.
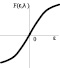
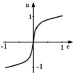
Теперь рассмотрим изменения степени пересечения выходной функции принадлежности. В третьей строке таблицы показаны функции с полным пересечением на входе и выходе, где результат почти линейно зависим. Изменение выходных функций принадлежности таким образом, чтобы они не пересекались, приведет к тому, что характеристика станет похожа на ту, что представлена в третьей строке таблицы, по сравнению с представленной в четвертой строке таблицы.
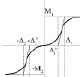
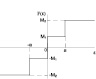
Поэтому можно предположить, что степень пересечения во входных функциях принадлежности сильно влияет на статические характеристики нечеткого регулятора. В то время как маленькие пересечения во входных функциях принадлежности формируют пороговые (ступенчатые) характеристики, большие пересечения делают кривую более гладкой. Пересечения выходных функций принадлежности меньше влияют на выходную характеристику регулятора. Как видно из приведенных графиков, характеристика, а следовательно, и качество управления зависит от используемой ФП и степени пересечений входных функций принадлежности оснований в выходной функции принадлежности. Существует достаточно большое количество подобных вариантов. Поскольку отсутствуют универсальные рекомендации по выбору этих пересечений, то актуальна задача их подбора для конкретных реализаций НР. Для решения этой задачи рассмотрим характеристики регулятора, полученные аппроксимацией нелинейностей и приведенные в таблице (столбец 4). В отличие от [6] в характеристиках аппроксимации учтены имеющиеся в реальных условиях ограничения, наложенные на управление. В столбце 5 таблице приведены статические характеристики нелинейных элементов, которые аппроксимированы отдельными сигмоидными функциями либо комбинацией сигмоидных функций [4]. Аналитические выражения для некоторых управляющих воздействий регулятора с этими функциями имеют вид
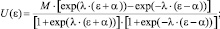 (1)
(1)
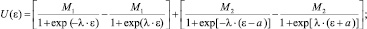 (2)
(2)
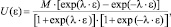 (3)
(3)
где U(ε) – регулирующеe воздействие; М, М1, М2 – величина регулирующего воздействия в зоне нечувствительности (ЗН) и за ее пределами соответственно; ε – ошибка регулирования; λ – параметр наклона линейного участка аппроксимирующей функции; 2а – величина зоны ЗН.
Виды функций принадлежности сигнала ошибки, управляющего воздействия и статические характеристики нечеткого и аппроксимирующего регулятора
|
Функции принадлежности сигнала ошибки |
Функции принадлежности управляющего воздействия |
Статические характеристики нечеткого регулятора |
Аппроксимирующие характеристики АНФ-регулятора |
Статические характеристики аппроксимируемого регулятора |
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как видно из графического сопоставления выходных зависимостей нечеткого регулятора и регулятора с аппроксимирующей характеристикой, названного нами АНФ-регулятором, можно установить близость этих характеристик. Причем каждая аппроксимирующая характеристика имеет аналитическое выражение, параметры которого определяют ее форму. Изменяя эти параметры, можно получить характеристику, наиболее близкую к выходной характеристике НР, которая и будет прототипом синтезируемого нечеткого АНФ-регулятора. В связи с использованием графического представления стратегии управления была поставлена задача создания нечёткого АНФ-регулятора с максимально простой структурой, который обеспечит необходимый вид зависимости «выхода от входа – характеристики управления». Для решения этой задачи в данной работе предлагается метод синтеза нечетких регуляторов САУ динамическими объектами, в основе которого использование аналитической зависимости управления от сигнала рассогласования, полученной с помощью аппроксимирующих преобразований нелинейных функций, доставляющей (обеспечивающей в) системе желаемый режим функционирования при номинальных параметрах объекта.
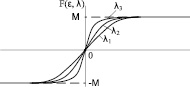
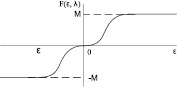
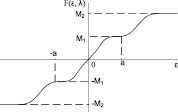
Комбинации нелинейностей, приводящие к получению необходимых зависимостей управления от сигнала рассогласования и реализуемые в нечетком регуляторе, положительно влияют на качество переходных процессов. При этом для повышения качества предлагается корректировать параметры закона аппроксимирующего управления. Например, характеристика на рис. 1, а (λ1 < λ2 < λ3) определяет стратегию управления с постоянной скоростью сигнала управления вблизи нулевой точки, на рис. 1, б – с уменьшением скорости сигнала по мере приближения к установившемуся значению, а на рис. 1, в – с увеличением скорости отклонения. Задав стратегию управления в виде характеристики аппроксимирующего управления, а также диапазоны изменения регулируемой переменной и управляющего воздействия, определяются такие значения параметров функций принадлежности, чтобы функциональная зависимость, которая реализуется нечётким регулятором, соответствовала этой характеристике.
а б
в
Рис. 1. Виды зависимостей управления от сигнала рассогласования
а
б
в
г
Исследовав влияние алгоритма нечёткого логического вывода, вида и расположения термов на осях лингвистических переменных, количества термов на входе и выходе регулятора, методов дефазификации и композиции, а также базы правил, получили наиболее простой по структуре нечёткий АНФ-регулятор, использующий алгоритм Мамдани, три функции принадлежности на входе и выходе, заданные треугольными, базу правил «если εk есть Аi и dεk/dt есть Bi, то uk есть Сi», дефаззификацию методом «центра тяжести».
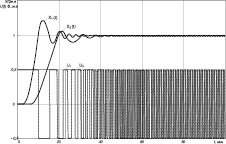
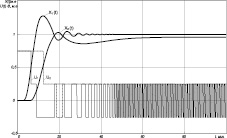
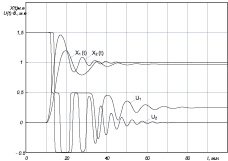
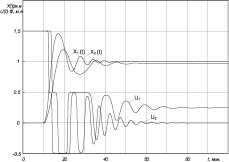
Рис. 2. Переходные процессы в астатической (Х1(t)) и статической (Х2(t)) системе с релейным управлением при значении М = 5 (а), М = 2,5 (б), с нечетким АНФ-регулятором при значениях М = 5 М1 = 0,5М; М2 = М; λ = 50; а = 0,5 (в) и значениях М = 10 М1 = 0,5М: М2 = М; λ = 50; а = 0,5 (г); по оси ординат отложены выходная переменная объекта и регулятора в машинных единицах (м.е.)
Результаты моделирования систем с релейным и аппроксимирующим управлением
Покажем, что регулятор с полученной структурой обеспечивает получение характеристики управления простого вида из ряда «гладких» кривых с несколькими точками перегиба и отсутствием разрывов. Для этого проведено моделирование систем с релейным управлением и с нечетким АНФ-регулятором. Рассмотрим переходные процессы в системе регулирования температуры в периодическом биореакторе для режима охлаждения среды в биореакторе с моделью объекта, характеризующегося отсутствием самовыравнивания, в виде уравнения
4d2у(t)/dt2 + dу(t)/dt = 0,05U(t – 6)
(кривая Х1(t)), и для режима с тепловыделением с моделью объекта в виде уравнения
73,08d2x(t)/dt2 + 14,35 dx(t)/dt + x(t) = = 0,383U(t – 6)
(кривая Х2(t)). Переходные процессы в системе управления с релейным управлением при равных значениях М1 = М2 = М представлены на рис. 2, а. Для уменьшения амплитуды автоколебаний в установившемся режиме уменьшено значение М1 в 2 раза. Переходные процессы в этой системе управления представлены на рис. 2, б. Как видно из полученных кривых переходного процесса, автоколебания для астатической системы сохраняются, а в статической системе имеет место остаточное отклонение. При этом сохраняется разрывной характер управляющего воздействия для обеих систем.
Для уменьшения автоколебаний и исключения разрывов в управляющем сигнале воспользуемся АНФ-регулятором с аппроксимирующей зависимостью управления (2). На рис. 2, в приведены переходные процессы в нелинейной системе при значениях параметров М1 = 2,5; М2 = 5,0. Как видно, колебательность в переходном процессе Х1(t) уменьшилась, переходный процесс Х2(t) приближен к апериодическому, характер управляющего воздействия – плавный и характеризуется колебательностью с сохранением статической ошибки. Увеличение значения М в 2 раза, как видно из рис. 2, г, обеспечивает незначительное уменьшение статической ошибки, увеличивая колебательность регулируемой переменной и управляющего сигнала. Переходный процесс колебательный и характеризуется выходом управляющего воздействия на предельные значения в начале переходного процесса. Поэтому дальнейшее увеличение М нецелесообразно.
Разработанный регулятор обеспечивает первоначальный быстрый выход в установившийся режим с плавностью перехода к установившемуся режиму, что необходимо для качественного управления многорежимными объектами и, в частности, при оптимальном управлении технологическими объектами биосинтеза.
Вывод
1. Применение зависимостей управления нечетких регуляторов в автоматическом управлении в сочетании с зависимостями, полученными на основе аппроксимирующих функций, позволяет существенно упростить процедуру подстройки регулятора традиционной САУ и обеспечивает повышение качества.
2. Управляющее воздействие в системе с нечетким аппроксимирующим регулятором не имеет резких выбросов или скачков на всем своём диапазоне, что обеспечивает лучшие условия работы исполнительных устройств управляемой системы.
Рецензенты:Червяков Н.И., д.т.н., профессор, зав. кафедрой математики и математического моделирования, ФГАОУ ВПО «Северо-Кавказский федеральный университет» Минобрнауки РФ, г. Ставрополь;
Федоренко В.В., д.т.н., профессор кафедры инфокоммуникаций, ФГАОУ ВПО «Северо-Кавказский федеральный университет» Минобрнауки РФ, г. Ставрополь.
Библиографическая ссылка
Лубенцова Е.В., Петраков В.А., Слюсарев Г.В., Лубенцов В.Ф. МЕТОД ПОСТРОЕНИЯ НЕЧЕТКИХ РЕГУЛЯТОРОВ С ИСПОЛЬЗОВАНИЕМ АНАЛИТИЧЕСКИХ ВЫРАЖЕНИЙ ДЛЯ УПРАВЛЯЮЩИХ ВОЗДЕЙСТВИЙ // Фундаментальные исследования. 2015. № 11-3. С. 484-490;URL: https://fundamental-research.ru/ru/article/view?id=39445 (дата обращения: 08.01.2026).