Явление электроконвекции в мембранных системах существенно увеличивает полезный массоперенос в процессах обессоливания разбавленных растворов. В связи с этим исследование факторов, способствующих интенсификации электроконвекции, является актуальной проблемой. В данной работе такое исследование проведено с использованием математической модели переноса ионов бинарной соли в канале обессоливания электродиализного аппарата с учетом электроконвекции являющей вариантом модели [9]. Эта модель состоит из уравнений Нернста – Планка – Пуассона и Навье – Стокса, являющихся представлением общих законов сохранений и краевых условий. Таким образом, именно краевые условия определяют конкретную модель. В данной работе дана физическая интерпретация краевых условий и проведен анализ влияния граничных условий на электроконвекцию. В качестве примера приведем влияние гидрофобности поверхности ионообменных мембран на перенос ионов соли и электроконвекцию. На гидрофобных поверхностях отталкивание молекул воды вызывает скольжение раствора по поверхности [3–5]. Длина скольжения меняется от нескольких нанометров [6] до нескольких десятков микрон [6, 7].
Кроме того, в некоторых моделях электроконвекции условие скольжения является естественным условием.
В данной работе на основе математического моделирования дана количественная оценка интенсификации электроконвекции в зависимости от длины скольжения раствора на поверхности ионообменных мембран.
При моделировании массопереноса в каналах без вынужденного течения часто применяются периодические условия, определяющие одинаковое распределение концентрационных, гидродинамического и электрического полей на входе и выходе канала. Учет вынужденного течения требует задания специальных условий на входе и выходе, которые обсуждаются ниже.
Геометрия задачи
В качестве примера мембранной системы рассмотрим камеру обессоливания (КО) электродиализного аппарата (ЭДА). В 2D случае она представляется прямоугольной областью, в которой левая граница x = 0 – анионообменная мембрана (АОМ), правая граница x = H – катионообменная мембрана (КОМ), вход в канал y = 0, выход из канала y = L.
Система уравнений
Система уравнений, описывающая массоперенос бинарного электролита в КО ЭДА:
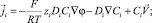 (1)
(1)
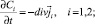 (2)
(2)
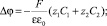 (3)
(3)
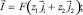 (4)
(4)
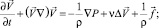 (5)
(5)
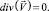 (6)
(6)
Здесь Ci, Di и zi – концентрация, коэффициент диффузии и зарядовое число i-го иона соответственно, i = 1 (катион) и i = 2 (анион); φ – потенциал электрического поля; 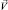 – скорость течения электролита; ρ – плотность электролита; P – давление; ε0 – диэлектрическая проницаемость вакуума; ε – относительная диэлектрическая проницаемость электролита; t – время; ν – кинематическая вязкость; F – постоянная Фарадея; R – универсальная газовая постоянная; T – температура.
– скорость течения электролита; ρ – плотность электролита; P – давление; ε0 – диэлектрическая проницаемость вакуума; ε – относительная диэлектрическая проницаемость электролита; t – время; ν – кинематическая вязкость; F – постоянная Фарадея; R – универсальная газовая постоянная; T – температура. 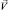 , P, φ, C1, C2 – это неизвестные функции t, x и y.
, P, φ, C1, C2 – это неизвестные функции t, x и y.
Краевые условия
1. Граничные условия на входе в канал (y = 0)
1) Условия для концентрации ионов. Будем считать, что на вход канала подается хорошо перемешанный раствор электролита (в конкретных расчетах водный раствор NaCl), так что концентрация катионов и анионов постоянна (7), причем выполняется условие электронейтральности (8).
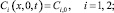 (7)
(7)
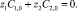 (8)
(8)
Из условия (8) следует
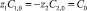 .
.
Ниже расчеты для раствора NaCl для которого 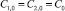 . Здесь C0 – концентрация электролита.
. Здесь C0 – концентрация электролита.
2) Условие на потенциал электрического поля. При выполнении условий (1) и (2) естественно предполагать, что через вход не втекает электрический ток, т.е. нормальная составляющая плотности тока равна нулю I2(t, x, 0) = 0. Из (6) и (2) с учетом (1) получаем, что при y = 0:
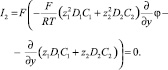
Следовательно, для потенциала получаем условие
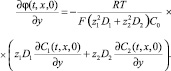 (9)
(9)
Если коэффициенты диффузии катионов и анионов примерно одинаковы, то и градиенты концентраций будут близки, тогда из (9) следует более простое граничное условие:
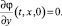 (10)
(10)
3) Условие на скорость течения раствора. Известно, что в прямоугольном канале при небольших числах Рейнольдса (средняя скорость V0 – небольшая) достаточно быстро устанавливается течение Пуазейля, когда тангенциальная составляющая равна нулю V1(t, x, 0) = 0, а нормальная является параболой Пуазейля. Поэтому положим V1(t, x, 0) = 0,
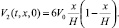
2. Граничные условия на выходе из канала (y = L)
1) Условия для концентрации ионов. На выходе из канала естественно предполагать, что ионы свободно выносятся потоком раствора (11) или (12).
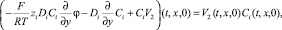 i = 1, 2; (11)
i = 1, 2; (11)
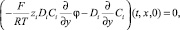 i = 1, 2. (12)
i = 1, 2. (12)
2) Условие на потенциал электрического поля. На выходе из канале, в отличие от входа, нельзя предполагать, что выполняется условие электронейтральности и отсутствует продольная составляющая тока. На выходе продольной составляющей тока является конвективный ток, следовательно (13). Откуда следует, что (14) или (15).
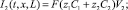 (13)
(13)
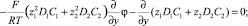 (14)
(14)
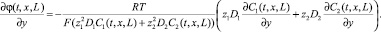 (15)
(15)
Очевидно, что условия (12) и (14) согласованы.
Граничное условие на выходе (14) аналогично условию на входе (9), но причины, приводящие к одинаковой формуле, различны.
3) Условие на скорость течения раствора.
Поскольку в данной задаче возможно возникновение нестационарных вихрей и на выходе из канала они должны свободно вытекать из канала, то неудачные граничные условия для скорости на выходе из канала обессоливания могут дать вычислительные артефакты близи выхода. Для решения этой проблемы нами используются два разных способа.
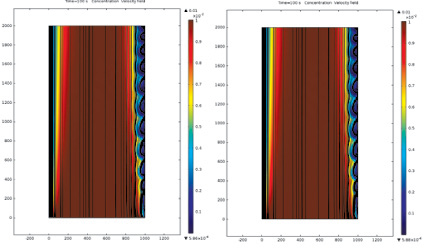
Первый способ – это удлинение канала и извлечение данных на некотором расстоянии перед выходом. В этом случае можно считать, что течение на выходе является также Пуазейлевским, если дополнительно задать давление в угловых точках. В этом случае электроконвективные вихри также свободно вытекают из канала (см. рис. 1, 2). Однако при моделировании гидрофобности поверхности мембран с помощью условия скольжения Навье нельзя использовать параболическое распределение Пуазейля. В этом случае можно задать постоянное давление p = 105 Пa.
Во втором способе мы считаем границу открытой, и на ней нормальное напряжение принимается равным нулю. В этом случае вихри могут свободно вытекать за пределы моделируемой области. При численных расчетах с таким условием возникают сложности с нахождением начального приближения в методе Ньютона, используемого для решения нелинейной системы уравнений в методе конечных элементов.
Из рис. 2 следует, что условия (1) и (2) в случае, когда на поверхности мембран задано условие прилипания, дают идентичные результаты.
4) «Мягкие» граничные условия на выходе. Поскольку на выходе из канала обессоливания концентрации не претерпевают резких изменений, вместо условия (11) можно использовать «мягкое» граничное условие (16). Тогда из (14) следует «мягкое» условие для потенциала (17).
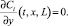 (16)
(16)
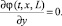 (17)
(17)
3. Граничные условия на поверхности ионообменных мембран
1) Условия для концентрации ионов
а) На поверхности анионообменной мембраны x = 0, y ∈ [0, L], t ≥ 0 будем считать граничную концентрацию анионов равной фиксированному заряду внутри мембраны:
C2(t, 0, y) = Cam. (18)
Кроме того, предположим анионообменную мембрану идеально селективной, т.е. непроницаемой для катионов:
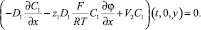 (19)
(19)
а б
Рис. 1. Линии тока раствора при различных условиях на скорость на выходе, рассчитаны в ППП «Comsol 5.1»: а – на выходе условие с параболическим распределением скорости вместе с давлением в угловых точках p(t, 0, L) = p(t, H, L) = p0; б – условие (9) с постоянным давлением
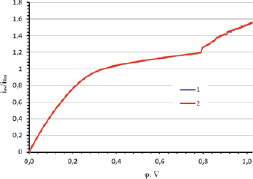
Рис. 2. Графики ВАХ: 1 – на выходе используется условие с параболическим распределением скорости вместе с давлением в угловых точках p(t, 0, L) = p(t, H, L) = p0; 2 – условие с постоянным давлением. Графики практически сливаются
б) На поверхности катионообменной мембраны x = H, y ∈ [0, L], t ≥ 0 будем считать граничную концентрацию катионов равной фиксированному заряду внутри мембраны:
C1(t, H, y) = Ccm. (20)
Кроме того, предположим катионообменную мембрану идеально селективной, то есть непроницаемой для анионов:
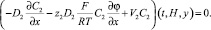 (21)
(21)
Обозначим для удобства 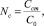
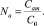 Здесь Na и Nc показывают во сколько раз Cam и Ccm больше, чем концентрация раствора C0.
Здесь Na и Nc показывают во сколько раз Cam и Ccm больше, чем концентрация раствора C0.
В работе [8] на основе 1D моделирования показано, что значение Ccm не влияет существенно на распределение концентрации и потенциала в области пространственного заряда. Это подтверждается расчетами ВАХ и течения раствора на основе 2D модели (рис. 3 и 4).
Таким образом, расчеты для больших значений Na и Nс не дают новой информации, однако значительно повышают трудоемкость вычислений. В связи с этим в большинстве расчетов ниже полагается Na = Nс = 1.
2) Варианты условий для скорости
Для скорости существуют различные варианты граничных условий на поверхности ионообменных мембран в зависимости от свойств мембран.
а) Если поверхность ионообменных мембран является смачиваемой, то тогда используется условие прилипания:
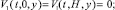
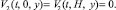 (22)
(22)
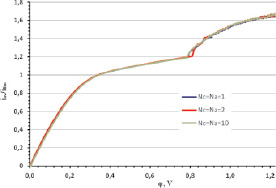
Рис. 3. Графики ВАХ для различных значений Na и Nc: a –Na = Nc = 1; б – Na = Nc = 2; в – Na = Nc = 10. Графики практически сливаются

а

б

в
Рис. 4. Линии тока раствора у КОМ при t = 100 s, Δφtot = 1В: а – Na = Nc = 1; б – Na = Nc = 2; в – Na = Nc = 10
б) Гидродинамическое условие скольжения
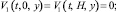
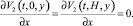 (23)
(23)
в) При моделировании гидрофобности поверхности мембраны используется условие скольжения Навье:
V1(t, 0, y) = 0; 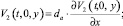 (24)
(24)
V1(t, H, y) = 0; 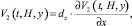 (25)
(25)
где da, dc – длина скольжения на поверхности анионообменной и катионообменной мембран. В приводимых ниже расчетах da = dc.
г) При моделировании электроконвекции в предположении электронейтральности раствора для области без вынужденного течения задают скорость электроосмотического скольжения второго рода в безразмерном виде:
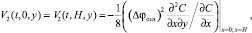
где Δφопз – скачок потенциала в системе (примерно равный скачку потенциала в области пространственного заряда); С – равновесная концентрация раствора.
Для следующих параметров: ширина диффузионного слоя 0,1 мм, длина L = 0,6 мм, начальная концентрация раствора С0 = 10 моль/м3, температура раствора T = 293 K, начальная плотность раствора ρ0 = 1002,5 кг/м3, коэффициент кинематической вязкости ν = 1006∙10–9 м2/с, коэффициенты диффузии катиона и аниона соответственно, D1 = 1,33∙10–9 м2/с, D2 = 2,05∙10–9 м2/с, разность потенциалов электрического поля в диффузионном слое dφ = –0,2 В, средняя скорость электроосмотического скольжения равна
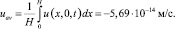
В связи с тем, что скорость электроосмотического скольжения мала, при достаточно больших скоростях вынужденного течения влияние условия скольжения незначительно.
Условие прилипания (22) и гидродинамическое условие скольжения (23) можно считать крайними случаями условия скольжения Навье (24), (25). Условие прилипания получается при da = dc → 0, а условие скольжения (23) при da = dc → ∞.
Из рис. 5 и 6 следует, что свойства поверхности ионообменных мембран существенно влияют как на перенос ионов соли, так и электроконвекцию.
3) Условие на скачок потенциала
Примем потоки в камерах обессоливания и концентрирования одинаково направленными. Будем также считать, что концентрация раствора в камере концентрирования во всех точках постоянна и равна Ck. Допустимость такого упрощения оправдана тем, что относительные изменения концентрации в этой камере значительно меньше изменений концентраций в камере обессоливания. Поэтому можно ожидать, что предлагаемое упрощение не окажет заметного влияния на точность расчета при произвольной гидравлической схеме и в то же время существенно уменьшит математические трудности.
Найдем скачок потенциала Δφtot на одной «парной» камере. Общее падение напряжения на мембранном пакете, состоящем из n «парных» камер, будет равно nΔφtot, т.е. параметр Δφtot может считаться известным.
Δφtot = Δφa + ΔφDC + Δφc,
где ΔφDC – разность потенциалов внутри камеры обессоливания, ограниченной x = 0 слева и x = h справа; Δφa – разность потенциала на анионообменной мембране и половине камеры обессоливания; Δφс – аналогичная величина, но для катионообменной мембраны.
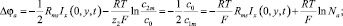 (26)
(26)
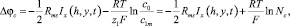 (27)
(27)
где Rms – общее омическое (мембраны + раствор) сопротивление системы, включающее анионообменную и катионообменную мембраны, а также камеру концентрирования: 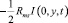 и
и 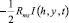 омические разности потенциалов в соответствующих частях системы при допущении, что сопротивление анионообменной и катионообменной мембран одинаково; Na и Nc показывают, во сколько раз c2m и c1m выше, чем концентрация электролита на входе (c0). Вторые слагаемые (26) и (27) включают в себя скачок потенциала на границе. Отсюда, для катионообменной мембраны имеем
омические разности потенциалов в соответствующих частях системы при допущении, что сопротивление анионообменной и катионообменной мембран одинаково; Na и Nc показывают, во сколько раз c2m и c1m выше, чем концентрация электролита на входе (c0). Вторые слагаемые (26) и (27) включают в себя скачок потенциала на границе. Отсюда, для катионообменной мембраны имеем
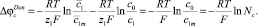 (28)
(28)
Устанавливая φ = 0 в центре левой части камеры концентрирования и учитывая, что φ(0, y, t) = Δφa и Δφtot = φ(h, y, t) + Δφc, из уравнений (12) и (13) находим
Δφtot = φ(h, y, t) + Δφc;
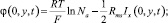
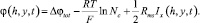 (29)
(29)
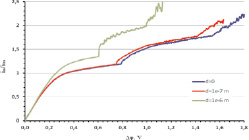
Рис. 5. Сравнение графиков ВАХ для условия прилипания и гидрофобности (d = 0; 10–7 м; 10–6 м)

а

б

в
Рис. 6. Линии тока раствора: a – d = 0 (условие прилипания); б – d = 10–7 м; в – d = 10–6 м
При вычислениях полагаем Δφtot линейно возрастающим с течением времени:
Δφtot = –αt,
где для большинства случаев α = 0,01 Vs–1.
4. Начальные условия
Будем предполагать, что в начальный момент времени в канале обессоливания течет раствор с некоторой средней скоростью V0. Поскольку в гладком канале достаточно быстро устанавливается течение Пуазейля, его можно использовать в качестве начального условия для скорости. Кроме того, будем предполагать, что в начальный момент концентрация раствора постоянна. Начальное условие для потенциала выбирается как линейная функция, соединяющая ее значения на поверхности ионообменных мембран.
В некоторых точках возможна несогласованность начальных и граничных условий. Обычно это достаточно быстро сглаживается и не приводит к артефактам.
Заключение
В работе сформулирована математическая модель переноса ионов соли с учетом электроконвекции, аналогичная модели [3], и дана физическая интерпретация краевых условий. Проведен анализ влияния граничных условий на электроконвекцию.
Исследование выполнено при финансовой поддержке РФФИ в рамках научных проектов № 13-08-93106-НЦНИЛ_а и 13-08-93105-НЦНИЛ_а.
Рецензенты:
Халафян А.А., д.т.н., доцент, профессор кафедры прикладной математики, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар;
Павлова А.В., д.ф.-м.н., доцент, профессор кафедры математического моделирования, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар.
Библиографическая ссылка
Коваленко А.В., Узденова А.М., Бостанов Р.А., Лайпанова З.М., Уртенов М.Х. АНАЛИЗ КРАЕВЫХ УСЛОВИЙ В МОДЕЛЯХ ЭЛЕКТРОКОНВЕКЦИИ В МЕМБРАННЫХ СИСТЕМАХ // Фундаментальные исследования. 2015. № 11-3. С. 444-451;URL: https://fundamental-research.ru/ru/article/view?id=39438 (дата обращения: 15.02.2026).
DOI: https://doi.org/10.17513/fr.39438



