Нестационарность инерционных и силовых параметров исполнительных устройств (ИУ) роботов является следствием взаимовлияния звеньев ИУ, изменения массы объекта манипулирования, величины припуска при абразивной зачистке и динамического передаточного отношения силового редуктора [5]. Задача обеспечения инвариантности к переменным инерционным и силовым параметрам решается применением комбинированного управления, систем с бесконечно большим коэффициентом усиления или глубокими обратными связями, систем с переменной структурой, систем и специальных алгоритмов как адаптивного управления, так и управления на основе обратных задач динамики [6, 7]. Внастоящей работе при решении вопросов структурно-алгоритмического построения электроприводов (ЭП) манипуляционных и технологических роботов (МР и ТР) с переменными инерционными и силовыми параметрами за основу принято адаптивное управление, высокая эффективность применения которого в робототехнике показана в работах [1, 2, 7].
Роботизация операций абразивной зачистки требует применения систем стабилизации мощности резания, реализуемых с помощью исполнительных ЭП. Вдвухдвигательных ЭП стабилизация мощности резания достигается за счет регулирования скорости ЭП главного движения или (и) скорости ЭП подачи. Воднодвигательных приводах эта задача решается, в частности, формированием как двухканальных, так и одноканальных управляющих сигналов.
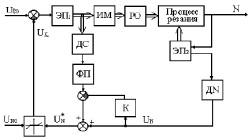
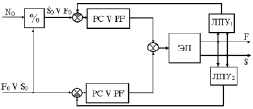
Двухдвигательные ЭП со стабилизацией мощности строятся [2] по схеме двухканального управления (рис.1,а). Сигнал UsO задает требуемую скорость перемещения РО робота, и UnO – с зоной нечувствительности определяют уровень стабилизируемой мощности. Сигнал корректирующей связи UK действует посредством уменьшения UsO при 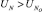 . Датчик скорости с функциональным преобразователем применяется для организации упреждающей коррекции.
. Датчик скорости с функциональным преобразователем применяется для организации упреждающей коррекции.
Двухканальные однодвигательные ЭП со стабилизацией NO строятся (рис.1,б) по аналогии с приводом изображенным на рис.1,а, в основе которого лежит применение технологических корректирующих связей. Другой путь, как уже отмечалось, заключается в формировании управляющих сигналов в функции NO=const (рис.1,в,г). Схема ЭП, представленная на рис.1,г, служит основой для построения ЭП двухзонного зависимого или независимого регулирования.
a
б
в
г
Рис.1. Функциональные схемы ЭП со стабилизацией мощности
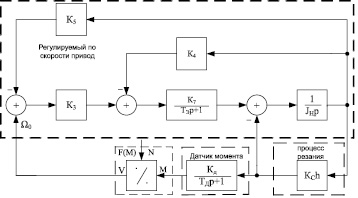
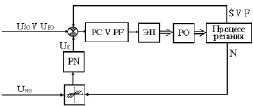
Рис.2. Структурная схема ЭП со стабилизацией мощности N, затрачиваемой на подачу
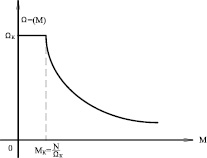
Рис.3. Нелинейный элемент F(M) типа «одноквадрантный делитель с ограничением»
Особое место занимают ЭП со стабилизацией мощности N, затрачиваемой на подачу. Вкачестве примера на рис.2 приведена структурная схема подобного привода [8].
Путем деления уставки по мощности NO на момент M от силы резания (рис.3) формируется сигнал задания по скорости ΩO (рис.2). Возможен и второй вариант привода, когда блок деления с уставкой NO, расположенный в контуре обратной связи по скорости, формирует сигнал задания по моменту MO.
Рассматриваемые приводы являются системами с параметрическим возмущением (т.е. с переменным параметром). Это следует из математической модели процесса резания. Поскольку возмущающим воздействием является изменение глубины резания, то при этом будет изменяться и коэффициент передачи объекта регулирования, а следовательно, и всего привода. Поэтому при синтезе необходимо учитывать изменения параметров Kc и h. Качество переходных процессов определяется как величиной припуска h (Kc=const), так и коэффициента усиления K3 по скорости. Так как коэффициенты уравнения динамики эти величины входят в обратно пропорциональной зависимости, то можно сделать вывод, что для поддержания заданных показателей качества необходимо изменять коэффициент K3 в зависимости от изменения h по следующей зависимости
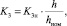
где K3н – коэффициент K3, рассчитанный для заданных показателей качества и при номинальной величине припуска hном. Очевидно, что максимальное значение K3 должно быть при максимальном припуске, а минимальное – при минимальном.
Для структурной схемы регулируемого ЭП передаточная функция по управляющему воздействию без учета K4 и нелинейного контура имеет вид
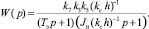
Откуда следует, что кроме общего коэффициента усиления с изменением припуска h, как уже отмечалось, изменяется постоянная времени T=Jн(kch)–1 в знаменателе передаточной функции W(p), что подобно изменению момента инерции Jн.
В [3] рассмотрен самонастраивающийся привод, у которого контурный коэффициент усиления изменяется вследствие изменения приведенного момента инерции. Так как изменение величины kch равноценно изменению момента инерции Jн, то данная структура может применяться для стабилизации контурного коэффициента в рассматриваемом приводе. На основании анализа работ по разработке адаптивных приводов МР была разработана структура наблюдателя момента инерции нагрузки Jн и припуска h [4], особенностью которой является более высокое быстродействие процесса оценки момента инерции и припуска по сравнению с известными структурами.
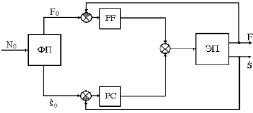
Структурная схема самонастраивающегося ЭП с наблюдателем параметра Jн(kch)–1 и стабилизацией мощности представлена на рис.4 [4].
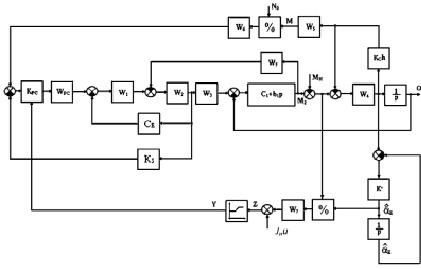
Рис. 4. Структурная схема самонастраивающегося ЭП с наблюдателем JН
W1=K7(Tэр+1)–1; W2=(J1p)–1; W3=(Up)–1;
W4=(Jнp)–1;W5=KД(Tдр+1)–1;
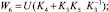 W7=U–1.
W7=U–1.
Таким образом, синтез привода состоит из двух этапов: синтеза главного контура в статике и динамике для некоторого расчетного усредненного значения (математического ожидания) величины припуска h и синтеза дополнительного контура самонастройки коэффициента K3 усиления регулятора скорости.
В приводе с нелинейностью F(M), обеспечивающей поддержание постоянной мощности подачи, коэффициент передачи аддитивной параметрической обратной связи изменяется так, что стабилизация общего коэффициента усиления осуществляется автоматически без необходимости изменения коэффициента усиления регулятора скорости.
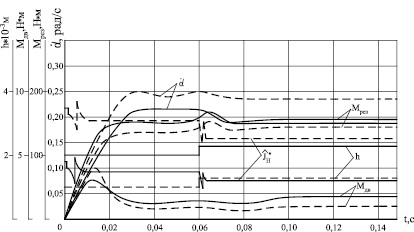
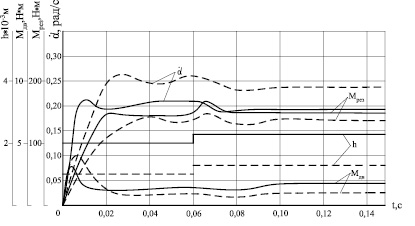
Графики переходных процессов в системе по структурной схеме ЭП с контуром самонастройки (рис.4) приведены на рис.5,а,б, откуда следует, что при изменении припуска h в 2раза качество переходных процессов сохраняется.
В системе без наблюдателя момента инерции переходные процессы по скорости и моменту становятся колебательными.
Полученные результаты моделирования системы с контуром самонастройки показывают эффективность использования алгоритма адаптации к переменной величине момента инерции и припуска при контурной обработке с постоянной мощностью.
а
б
Рис.5. Переходные процессы в ЭП:а – переходные процессы в ЭП с контуром самонастройки; б – переходные процессы в ЭП без контура самонастройки
Работа выполнена при финансовой поддержке РФФИ (проект №13-08-01364).
Библиографическая ссылка
Рассказчиков Н.Г., Егоров И.Н., Назаров А.А. ВОПРОСЫ РАЗРАБОТКИ ПРИВОДОВ РОБОТОВ С ПЕРЕМЕННЫМИ ИНЕРЦИОННЫМИ И СИЛОВЫМИ ПАРАМЕТРАМИ // Фундаментальные исследования. 2015. № 12-2. С. 325-330;URL: https://fundamental-research.ru/ru/article/view?id=39414 (дата обращения: 08.02.2026).



