Быстрый рост объемов обработки данных, развитие цифровых систем вещания и вычислительных сетей предъявляют высокие требования к минимизации ошибок в используемых цифровых данных. Поэтому одной из важнейших задач является обеспечение высокой достоверности передачи данных. Исправлением ошибок после передачи по каналу занимается помехоустойчивое кодирование [2].
Одним из наиболее эффективных решений проблемы помехоустойчивого кодирования при высокой энергетической характеристике систем кодирования являются многопороговые декодеры, которые позволяют декодировать очень длинные коды с линейной от длины кода сложностью исполнения. Воснове работы МПД лежит итеративное декодирование, что позволяет вплотную приблизиться к решению оптимального декодера в достаточно большом диапазоне кодовых скоростей и уровней шума в канале. При этом МПД сохраняет простоту и быстродействие обычного порогового декодера, что делает его очень привлекательным для применения в существующих и вновь создаваемых высокоскоростных системах связи [3].
Схема работы МПД представлена на рис.1.
Главное достоинство МПД, которые были сначала разработаны для двоичных кодов, заключается в том, что используемые в них мажоритарные процедуры коррекции ошибок допускают полное распараллеливание выполняемых операций, что обеспечивает работу с теоретически максимально возможной производительностью.
Моделирование
Для оценки эффективности помехоустойчивых кодов и методов их декодирования при большом уровне шума требуется использовать моделирование, поскольку аналитическая оценка вероятности ошибки в таких условиях является обычно очень неточной. Особенностью современных систем передачи и хранения данных является низкая целевая вероятность ошибки. Например, в оптических системах связи необходимо обеспечить вероятность ошибки менее 10–11. Для оценки подобной вероятности ошибки с помощью моделирования нужно выполнить передачу как минимум 1012битов. Вместе с тем моделирование кодирования, передачи и декодирования подобных объемов данных является очень затратной с временной точки зрения операцией. Кпримеру, при использовании вычислительных ресурсов центрального процессора (CPU) удалось получить скорость передачи данных по каналу связи с МПД только на уровне 320кбит/с. Для эксперимента использовался процессор Intel(R) Core(TM) i3 2,53GHz (двухъядерный процессор). Во время моделирования удалось достичь практически 100 % загрузки обоих ядер CPU. При такой скорости моделирование передачи 1012бит через канал связи займет около 868 часов. Подобные временные затраты являются неприемлемыми.
Исходя из вышесказанного необходимо найти возможности по увеличению скорости моделирования систем передачи данных.
Задача ускорения вычислений требует использования принципиально других подходов к организации вычислений. Перспективным направлением ускорения вычислений является использование незадействованных ресурсов гетерогенных компьютерных систем, в частности вычислительных ресурсов графических процессоров GPU (graphic processing unit). Вслучае достаточного параллелизма реализуемых вычислений применима техника General-purpose computing forgraphics processing units (GPGPU) [4]. Такую технику можно использовать и для моделирования работы МПД.
Отметим, что время моделирования можно грубо оценить как
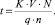
Здесь t – время моделирования; V – число передаваемых бит; N – число элементарных операций, требующихся на передачу одного бита; n – число ядер в процессоре; q – тактовая частота процессора; K – коэффициент накладных расходов. При количестве ядер процессора n больше единицы коэффициент будет меньше единицы. Это связано с ростом числа инфраструктурных операций, выполняемых CPU для синхронизации параллельной работы ядер. Данные инфраструктурные операции будут уменьшать общий объем полезных операций, выполняемых GPU. При использовании процессором одного ядра K будет равен единице, так как все вычислительные ресурсы будут направлены на целевые операции.
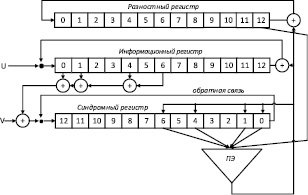
Рис. 1. Многопороговый декодер блокового кода
Обычно вопрос времени моделирования описывался простым правилом – чем больше частота, тем больше производительность. Однако бесконечный рост тактовой частоты невозможен. Это связано с конструктивными сложностями, в частности с проблемой перегрева процессора. Исходя из этого можно сделать вывод, что альтернативным ресурсом повышения скорости моделирования является увеличение числа ядер в процессоре. Однако потенциал роста числа ядер в CPU ограничен. CPU с числом ядер16 и больше являются большой редкостью и имеют высокую стоимость. Однако большое число ядер можно найти в GPU. ВGPU число ядер может достигать нескольких тысяч, что позволяет рассмотреть использование GPU в качестве перспективного вычислительного механизма для решения вышеописанной задачи.
Использование GPGPU
В настоящее время для вычислений на GPU активно продвигаются две технологии OpenCL и CUDA.
OpenCL (OpenComputingLanguage) – это технология, реализующая параллельные компьютерные вычисления на различных типах графических и центральных процессоров.
CUDA (ComputeUnifiedDeviceArchitecture) – программно-аппаратная архитектура параллельных вычислений, которая позволяет существенно увеличить вычислительную производительность благодаря использованию графических процессоров фирмы Nvidia [1].
Обе описанные технологии представляют схожий функционал для активного и эффективного использования вычислительных ресурсов GPU. Существенным отличием является то, что CUDA поддерживается и продвигается преимущественно компанией Nvidia, следовательно, для моделирования с иcпользованием CUDA понадобится персональный компьютер c GPU производства именно этой компании. Данный факт существенно сужает парк компьютеров, который может использоваться для моделирования. Вто же время OpenCL поддерживается практически всеми производителями GPU (включая Nvidia), ничуть не уступая в эффективности. Исходя из этого выбор OpenCL для моделирования работы является очевидным.
Синтаксис языка программирования OpenCL базируется на стандарте C99, но имеет ряд специфических и очень важных изменений. Подобные изменения накладывают ряд значительных ограничений [5]:
–невозможно динамическое выделение памяти;
–невозможно использовать массивы с размерностью более единицы;
–невозможно использование рекурсий;
–отсутствие встроенного генератора случайных чисел.
Данные ограничения привели к необходимости нестандартных инженерных решений при программировании работы МПД на языке OpenCL.
Одно из решений связано с разработкой структуры, реализующей работу двумерного массива, который необходим при моделировании работы МПД. Структура представляет из себя одномерный массив, который содержит элементы нескольких одномерных массивов и некоторую инфраструктурную информацию. Структура, представленная на рис.2, состоит из 4частей:
–общее количество одномерных массивов в структуре;
–общая длина структуры;
–длины одномерных массивов, содержащихся в структуре;
–элементы одномерных массивов, входящих в структуру.
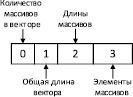
Рис. 2. Схема структуры для хранения одно- или двумерных массивов
Для одномерного массива длиной2, содержащего элементы [0, 3], структура будет иметь вид, представленный на рис.3.

Рис. 3. Структура, хранящая одномерный массив
Если нужно использовать двумерный массив, то необходимо в структуру просто поместить два одномерных массива. Для двух одномерных массивов длиной2, содержащих элементы [0, 3] и [1, 11], структура будет иметь вид, представленный на рис.4.
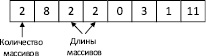
Рис. 4. Двумерный массив в структуре
Так же был реализован генератор случайных чисел на основе регистров сдвига с обратной связью. Принцип действия генератора заключается в смещении и маскировании случайной величины. Начальное случайное значение задается при старте приложения.
Реализация генератора на языке OpenCL, для заполнения массива случайных чисел, представлена в листинге.
Листинг

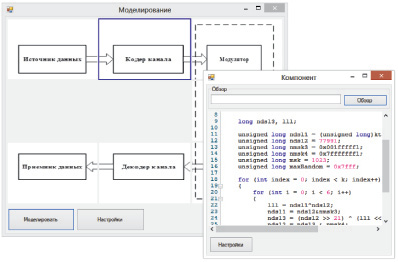
Рис. 5. Интерфейс десктоп-приложения для моделирования
Данный генератор позволяет получить случайные числа с равномерным законом распределения в диапазоне [0; 1).
Описанная выше структура для хранения данных и генератор случайных чисел были использованы в десктоп-приложении, разработанного для моделирования работы МПД с использованием GPU. Одна из форм приложения представлена на рис.5.
Данное приложение максимально эффективно использовало ресурсы GPU и позволило увеличить скорость моделирования передачи данных по каналу связи с МПД до 11мбит/с. Таким образом, по сравнению с реализацией через CPU скорость моделирования была увеличена в 34раза. При такой скорости моделирование передачи 1012бит через канал связи с кодированием и декодированием займет всего около 25часов, что значительно меньше времени, затраченного при моделировании передачи данных с использованием CPU. Вданном эксперименте использовался GPU AMD Radeon HD6300M Series c 128ядрами в процессоре.
Вывод
Полученные результаты дают основание считать перспективным использование предложенного подхода к решению задачи уменьшения временных затрат на ресурсоемкое моделирование характеристик МПД. Существующие результаты имеют широкий потенциал для дальнейшего алгоритмического улучшения. Так же очевиден легко извлекаемый аппаратный потенциал, который позволит повысить скорость моделирования за счет использования более мощных GPU, которые в настоящее время широко доступны.
Работа выполнена при поддержке РФФИ (грант №13-07-00391) и гранта Президента РФ (грант МД-639.2014.9).
Библиографическая ссылка
Демидов Д.С., Овечкин Г.В. МОДЕЛИРОВАНИЕ СИСТЕМЫ ПЕРЕДАЧИ ДАННЫХ С МНОГОПОРОГОВЫМ ДЕКОДЕРОМ С ИСПОЛЬЗОВАНИЕМ OPENCL // Фундаментальные исследования. 2015. № 12-2. С. 243-247;URL: https://fundamental-research.ru/ru/article/view?id=39398 (дата обращения: 14.03.2026).



