Работа относится к машиностроению и посвящена автоматизации контурной обработки деталей изделия легкой промышленности.
Целью исследования является изучение технологических возможностей ФТОУ при контурной обработке. Вработе приведены результаты исследования технологической возможности ФТОУ и пути их расширения.
Основные пути высокоэффективной технологии и средств, выполняющих эту технологию – создание автоматизированной машины – направлены на повышение производительности за счет ускорения скоростных режимов выполнения контурных строчек с использованием программных устройств. Разработанные к настоящему времени устройства для реализации указанных операций разнообразны по используемым рабочим органам и характеру движения деталей. Однако они далеко не всегда обладают требуемой технологической гибкостью, часто сложны по конструкции и вобслуживании и, как правило, имеют большую стоимость.
Известно, что доля ручного труда при выполнении технологических операций по производству изделия легкой промышленности ещё велика. Восновном сборка заготовок изделия легкой промышленности, в том числе обувного, швейного, кожгалантерейного и мехового производства осуществляется на машинах общего назначения, где ориентация края деталей относительно иглы осуществляется вручную. Зачастую эти обстоятельства затрудняют повышение производительности и качества труда.
В связи с этим создание простого по конструкции, надежного в эксплуатации и технологически гибкого средства является наиболее экономичным путем решения задачи автоматизации сборки изделия.
Нами предлагается автоматизированная швейная машина (АШМ), основанная на том, что контур является программой для работы машины [1–4], а не наоборот, как у известных аналогов, где программа является основой для выполнения операции. Данный способ и АШМ аналогов не имеют. АШМ за счет ФТОУ, в зависимости от величины и знака обрабатываемого контура, автоматически перемещает деталь с поворотом по часовой, против часовой стрелки или прямолинейно.
Задача состоит в том, что необходимо выбрать параметры ФТОУ так, чтобы обеспечивалось выполнение технологических требований, как обработка минимальных кривизны контуров и качества выполнения контурной строчки.
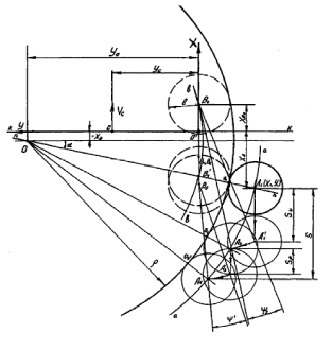
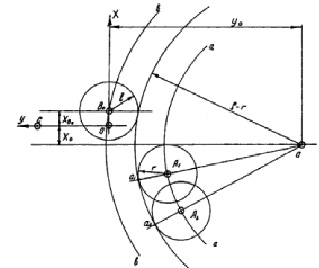
Технологические возможности рассматриваемого способа ориентации детали определяются, очевидно, минимальным радиусом (ρmin) ее кривизны [5]. Исходя из того, что координаты т.A1(X1, X2) центра упора задаются необходимым расстоянием строчки от края (l=1,0–1,5мм) детали (рисунок,а). Отметим также, что контур любой формы может быть с достаточной для практических целей точностью представлен в виде отрезков дуг окружностей и прямых. Процесс обработки прямолинейной части контура интереса не имеет, поэтому ниже рассмотрим участок контура, представляющий собой часть круга (рисунок) [6–8].
Рассмотрим случай «выпуклой» кривизны. Пусть ось ОУ (рисунок) совпадает с линией (k–k), проведенной параллельно оси роликов в точке (С) соприкосновения их с деталью, а ось ОХ – параллельна направлению перемещения иглы B1B2. Координаты точки B0(Xb0; 0) начала прокола иглой материала также задаются из технологических требований, а именно величины шага стежка. Координаты точки C(Xc, Yc) задаются произвольно.
Составим уравнение окружности (a–a) с центром O(–X0, Y0), радиусом (ρ+r), проходящей через т.т.A1 и A2 (рисунок,а):
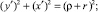
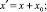
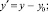
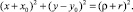
Учитывая, что упор имеет радиус r, запишем уравнение окружности радиуса (ρ+r), проходящей через точку A1, с центром в точке O, относительно коор динат XOY:
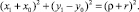 (1)
(1)
Уравнение той же окружности, учитывая, что она проходит и через точку A2, можно записать в виде
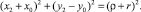 (2)
(2)
Отметим, что здесь мы используем обращенный метод перемещения детали, поэтому точка A2 представляет собой новый центр упора после окончания ориентирования детали.
Через точку B0 из того же центра 0 можно провести окружность (b–b) радиусом (ρ – l). Ее уравнение
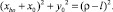 (3)
(3)
Используя систему уравнений (1), (2)и (3), приходим к уравнению
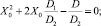
корень которого, соответствующий минимальному радиусу кривизны контура, определяется как
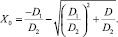 (4)
(4)
Подставив полученное выражение в (3), получим значение:
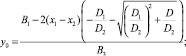 (5)
(5)
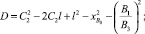
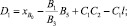
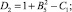
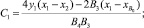
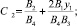
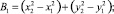
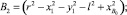
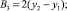
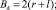
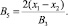
а
б
Процесс перемещения:а – детали; б – «вогнутого» контура
Таким образом, мы получили координаты центра окружности минимального радиуса для «выпуклой» кривизны. Тогда величина радиуса этой окружности определяется как
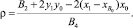 (6)
(6)
После элементарных преобразований с учетом (5) и (6) окончательно получаем минимально допустимое значение радиуса «выпуклой» кривизны контура детали, при которой предлагаемый способ ориентации будет реализован (рисунок,а):
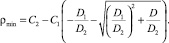 (7)
(7)
Для случая «вогнутой» кривизны ход рассуждений аналогичен, поэтому выкладки опустим. Соотношения, определяющие координаты геометрического центра детали в данном случае, имеют вид (рисунок, б):
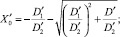 (4′)
(4′)
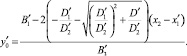 (5′)
(5′)
Тогда минимальное значение радиуса «вогнутой» кривизны определяется соотношением
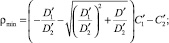 (7′)
(7′)
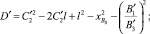
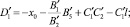
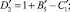
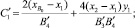
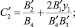
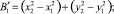
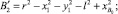
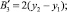
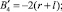
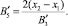
Получены аналитические зависимости (7) и (7′), определяющие значения минимальной кривизны перечисленных контуров, в зависимости от координаты расположения упора, расстояния расположения строчки от края детали, величины шага стежка, места расположения роликов, начала прокола иглой материала и радиусом упора.
Выводы
Полученные аналитические зависимости позволяют, определить технологические возможности автоматизированной швейной машины, реализующих предлагаемый способ ориентирования детали. Расчет по этим зависимостям показывает, что минимальный радиус контура детали составляет 7 и 5мм соответственно для «выпуклой» и «вогнутой» кривизны при расстоянии строчки от края не менее 1,2мм, что вполне устраивает технологические требования к выполнению краевых строчек на изделиях легкой промышленности. Итак, при правильном выборе параметров вновь созданного ФТОУ модернизируемая швейная машина может быть применена для автоматизированного выполнения контурных строчек.
Библиографическая ссылка
Баубеков С.Д., Баубеков С.С., Таукебаева К.С. ОПРЕДЕЛЕНИЕ ТЕХНОЛОГИЧЕСКОЙ ВОЗМОЖНОСТИ ФРИКЦИОННО-ТРАНСПОРТНО-ОРИЕНТИРУЮЩЕГО УСТРОЙСТВА (ФТОУ) ДЛЯ АВТОМАТИЗИРОВАННОЙ КОНТУРНОЙ ОБРАБОТКИ // Фундаментальные исследования. 2015. № 12-2. С. 233-237;URL: https://fundamental-research.ru/ru/article/view?id=39396 (дата обращения: 15.02.2026).



