•Проблема навигации БПЛА с помощью средств, методов и алгоритмов компьютерного зрения активно исследуется в течение последних нескольких десятилетий. В ИПС им. А.К. Айламазяна РАН был разработан алгоритм решения задачи позиционирования БПЛА для полетов над плоской местностью, основанный на сопоставлении так называемых особых точек, найденных на кадре видеоряда и на эталонном снимке местности (полученном с искусственного спутника Земли – ИСЗ) [5]. В целях оптимизации процедуры сопоставления и решения проблемы различия масштабов между двумя изображениями для спутникового снимка строится так называемая пирамида изображений, каждый слой пирамиды разбивается на фрагменты (тайлы, англ. tiles) [3]. В силу невозможности проводить эксперименты с БПЛА из-за их высокой стоимости разработанные алгоритмы тестировались на виртуальных видеорядах – результатах моделирования полета БПЛА с помощью методов и алгоритмов компьютерной графики.
Исследования были продолжены в сторону разработки методов и алгоритмов позиционирования для случая, когда рельефом местности пренебречь нельзя. Задачу позиционирования по снимку предлагается свести к задаче внешней калибровки камеры на БПЛА [1], для этого необходимо найти на кадре координаты нескольких опорных точек с известными 3D-координатами в геоцентрической системе координат.
Кратко рассмотрим методы поиска точечных объектов на изображениях. Корреляционно-экстремальные методы основаны на решении оптимизационной задачи: максимизации меры сходства между эталонным изображением опорного объекта и изображением, на котором производится поиск объекта. Описание подобных методов доступно, например, в работе [9], однако корреляционно-экстремальные методы слабо инвариантны к яркостным и геометрическим преобразованиям [6].
Вторая группа методов основана на выделении контуров и поиске структурных особенностей (прямых линий, прямоугольников, эллипсов, окружностей). Например, в работе [2] выполняется поиск характерных точек изгибов контуров и сопоставление отдельных участков контуров. Однако подобные методы скорее подходят для антропогенных территорий, поскольку фотографии естественных ландшафтов (поля, леса, реки, возвышенности) редко содержат правильные геометрические фигуры и прямые линии.
Третья группа методов основана на предварительном выделении на эталонном изображении так называемых особых точек, для каждой из которых вычисляется ее дескриптор (описатель). Дескрипторы затем сравниваются с дескрипторами особых точек, найденных на обрабатываемом изображении [7, 11]. Недостаток такого подхода состоит в том, что если выбранная на изображении опорная точка (одиноко стоящее дерево, вершина горы, специально подготовленная искусственная метка) не распознана алгоритмом в качестве особой, то вычислить дескриптор для нее не удастся.
Цель настоящего исследования – разработать устойчивый алгоритм поиска опорных точек на изображениях – высотных снимках естественных ландшафтов.
Материалы и методы исследования
Вейвлеты Габора: описание и методика использования в задаче поиска опорных точек
В различных алгоритмах обработки и анализа изображений широко применяются фильтры (вейвлеты) Габора: для распознавания радужной оболочки в биометрических системах безопасности и в автоматизированных системах контроля доступа на основании распознавания отпечатков пальцев. Вейвлеты устойчивы к изменениям яркости и геометрическим искажениям [6]. Импульсная переходная характеристика таких фильтров имеет следующий параметрический вид:
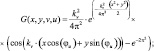
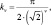 v = {0, 1, ..., 4}; (1)
v = {0, 1, ..., 4}; (1)
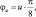 u = {0, 1, ..., 7}.
u = {0, 1, ..., 7}.
Параметр v определяет масштаб фильтра, u – его ориентацию. Таким образом, получаем семейство из 40 фильтров Габора. Результаты свертки некоторой области изображения с каждым из фильтров образуют 40-мерный вектор – так называемый джет, который можно использовать в качестве дескриптора того пикселя, который лежал в центре области. Сравнение джетов с двух изображений позволяет сопоставлять точечные особенности между ними: например, в работе [6] в качестве меры близости между двумя джетами использовался косинус угла между векторами. В данной работе в качестве первого изображения выступает эталонный снимок местности, на нем выбираются опорные точки, для которых вычисляются джеты Габора. Второе изображение – кадр видеоряда с камеры на БПЛА.
Выбор опорных точек на спутниковом снимке
На эталонном снимке местности необходимо выбрать ряд опорных точек таким образом, чтобы на снимках с БПЛА точки были наблюдаемы в количестве, достаточном для решения задачи внешней калибровки. Поскольку все эксперименты проводились со сгенерированными по трехмерным моделям земной поверхности видеорядами, то был разработан следующий подход. В ходе предварительной подготовки данных на каждом тайле находились особые точки с помощью алгоритма SURF. Каждый тайл делился на 4 части, и в каждой из них выбиралось по одной опорной точке с наибольшим значением определителя матрицы Гессе. Такой определитель является одним из описателей особой точки: чем он больше, тем лучше она выделяется на фоне пикселей-соседей [7]. Эти точки принимались в качестве опорных, затем для каждой из них вычислялись ее трехмерные координаты (с помощью доступной карты высот). Эксперименты показали, что для достижения приемлемой точности позиционирования БПЛА достаточно найти на видеокадре около 10 опорных точек.
Сужение области поиска опорной точки и ректификация видеокадра
Поиск даже одной опорной точки на всем снимке с БПЛА (который может иметь разрешение в несколько мегапикселей) является достаточно ресурсоемкой задачей. Область поиска можно существенно уменьшить, если принять во внимание тот факт, что в промежуток времени между двумя смежными кадрами БПЛА пролетает относительно небольшое расстояние, его максимально возможная скорость ограничена, а для предыдущего кадра видеоряда положение (вектор Tprev) и ориентация (матрица Rprev) камеры на БПЛА уже найдены. Это позволяет вычислить координаты q0 проекции опорной точки на предыдущем кадре и ограничить область поиска опорной точки окружностью некоторого радиуса sr, центр которой – точка q0. Радиус зависит от фокальной длины камеры, от максимально возможной скорости БПЛА и от высоты полета в предыдущий момент времени [4]. Но если положение БПЛА между двумя соседними моментами съемки не может существенно поменяться, то навигационные углы (тангаж, крен и особенно рысканье), определяющие ориентацию аппарата, могут значительно меняться между кадрами в случае выполнения различных маневров. Использование Rprev и Tprev приведет к тому, что спрогнозированное положение опорной точки на текущем кадре будет находиться на значительном удалении от ее истинного положения. Другая проблема заключается в том, что вейвлеты Габора инвариантны к геометрическим искажениям, но только в относительно небольших пределах [6].
Был разработан метод ректификации снимков с БПЛА и вычисления примерных координат опорной точки на текущем кадре с точностью, достаточной для последующего поиска точных координат опорной точки с помощью вейвлетов Габора. Вначале опишем метод прогнозирования координат БПЛА в текущий момент времени. На рис. 1 показана система координат, привязанная к летательному аппарату. Камера закреплена и смотрит вниз. Система координат OX1Y1Z1, привязанная к камере, ориентирована таким образом, что луч OX1 совпадает с лучом OZ, луч OY1 направлен противоположно лучу OX, а луч OZ1 – противоположно лучу OY. Столбцы матрицы Rprev определяют координаты базисных векторов OX1, OY1, OZ1, привязанных к камере, относительно глобальной системы координат. В частности, второй столбец r2 матрицы Rprev – координаты базисного вектора OY1, он противоположен направлению движения аппарата. Если V – расстояние, которое пролетает БПЛА за промежуток времени между двумя смежными кадрами (с учетом скорости в предыдущий момент времени), то спрогнозированное положение БПЛА в текущий момент времени можно вычислить следующим образом:
Tcurr_app = Tprev + V•(–r2).
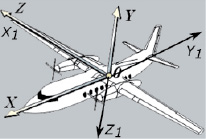
Рис. 1. Связанная система координат и система координат камеры
Далее, вычисляется так называемая фундаментальная матрица F [10], связывающая координаты пар соответствующих особых точек на ИСЗ и БПЛА, найденных алгоритмом SURF. Производится декомпозиция матрицы F на матрицу поворота R (определяет взаимную ориентацию камер на ИСЗ и БПЛА) и вектор T (определяет их взаимное положение, но с точностью до некоторого неизвестного положительного коэффициента). Проводится декомпозиция матрицы R на три угла поворота φ, ψ, θ. Угол θ принимается в качестве примерного значения угла рысканья БПЛА в текущий момент времени и вместе с углами φprev и ψprev (тангаж и крен для предыдущего кадра) используется для построения матрицы Rrect, которая затем используется для ректификации кадра с БПЛА. С помощью Tcurr_app и Rrect вычисляется матрица Rcurr_app – спрогнозированная матрица ориентации камеры на БПЛА в текущий момент времени.
Каждому слою пирамиды спутниковых снимков v1...vM соответствует некоторая ориентировочная высота hi полета БПЛА (иначе говоря, если БПЛА поместить на высоту hi, то снимки с камеры будут точно в таком же масштабе, что и слой vi пирамиды) [3]. Для предыдущего кадра высота полета БПЛА уже вычислена и равна 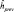 , высота опорной точки над уровнем моря равна
, высота опорной точки над уровнем моря равна 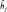 (напомним, что 3D координаты всех опорных точек известны). Тогда расстояние от поверхности Земли до положения БПЛА в предыдущий момент времени равно
(напомним, что 3D координаты всех опорных точек известны). Тогда расстояние от поверхности Земли до положения БПЛА в предыдущий момент времени равно 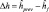 . Область поиска опорной точки имеет относительно небольшие размеры, и поэтому перепадами высот на ней можно пренебречь. Проективные преобразования плоскости описываются матрицей гомографии H [10]. Ректификацию кадра с БПЛА предлагается выполнять с помощью следующей матрицы:
. Область поиска опорной точки имеет относительно небольшие размеры, и поэтому перепадами высот на ней можно пренебречь. Проективные преобразования плоскости описываются матрицей гомографии H [10]. Ректификацию кадра с БПЛА предлагается выполнять с помощью следующей матрицы:
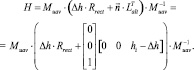 (2)
(2)
Здесь Muav – матрица внутренних параметров камеры на БПЛА. Действие такой матрицы гомографии на изображение можно интерпретировать как изменение положения и ориентации камеры, наблюдающей плоскую сцену. Матрица Rrect отвечает за смену ориентации, вектор Lalt – за смену положения (в данном случае изменяется высота). Матрица H преобразует снимок в такой «канонический» вид, когда камера БПЛА направлена перпендикулярно поверхности Земли и имеет ту же ориентацию, что и снимок с ИСЗ. Кроме того, снимок масштабируется так, как если бы он был выполнен с высоты hi, т.е. снимок теперь выполнен в том же масштабе, что и один из слоев пирамиды спутниковых снимков.
Таким образом, ректификация компенсирует различия снимков с БПЛА и ИСЗ в ориентации и масштабе и позволяет проводить поиск опорных точек на кадре видеоряда с помощью вейвлетов Габора. Для наглядности приведем ряд иллюстраций. На рис. 2 приведен пример тайла спутникового снимка, опорная точка лежит в центре белой окружности (размер тайла – 256×256 пикселей).

Рис. 2. Тайл спутникового снимка с опорной точкой
На рис. 3 – пример видеокадра с борта БПЛА (в экспериментах использовалось разрешение 1024×768 пикселей). Спрогнозированное положение опорной точки с 3D координатами P показано белой окружностью, координаты ее проекции равны
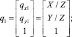
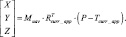 (3)
(3)
На рис. 4 приведен результат ректификации видеокадра. Область поиска опорной точки является квадратом, который выделен белым цветом. Координаты его угловых точек равны
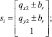
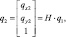
i = 1...4, br = sr + qr. (4)
Здесь q2 – спрогнозированные координаты опорной точки на преобразованном кадре; gr – ширина и высота квадратных масок для дискретизированных фильтров Габора. На рис. 2 эта же область поиска выглядит как четырехугольник (проективное преобразование квадрата) с координатами угловых точек 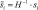 . Для ускорения вычислений достаточно проводить ректификацию не всего изображения, а только его небольшой части, попадающей в четырехугольную область на рис. 2.
. Для ускорения вычислений достаточно проводить ректификацию не всего изображения, а только его небольшой части, попадающей в четырехугольную область на рис. 2.

Рис. 3. Видеокадр с борта БПЛА с выделенной областью поиска опорной точки

Рис. 4. Ректифицированный видеокадр с борта БПЛА с выделенной областью поиска опорной точки
Результаты исследования и их обсуждение
Все разработанные алгоритмы были реализованы в виде программ на языке C++, вычисления выполнялись на одном из ядер процессора Intel Xeon E5410. Использовался спутниковый снимок размером 10000×10000 пикселей (пространственное разрешение – 1 метр на пиксель) и карта высот размером 10000×10000 пикселей (10 метров на пиксель). В табл. 1, 2 и 3 приведены результаты тестов по применению вейвлетов Габора в задаче позиционирования БПЛА по сгенерированному видеоряду. В качестве траекторий полета виртуального БПЛА использовались маршруты на высотах 300, 500, 1000, 1200, 1500, 2000 и 2500 метров. Маршруты строились таким образом, чтобы они содержали и участки прямолинейного полета на постоянной высоте (с различными углами рысканья), и участки маневрирования (изменение курса или высоты полета). Также варьировался параметр gr. Вычислялось время поиска одной опорной точки на снимке с БПЛА (в миллисекундах), погрешность в определении координат опорной точки (в пикселях), а также максимальная погрешность в определении положения БПЛА по всем кадрам видеоряда (в метрах). Все значения – усредненные по результатам серии запусков для различных траекторий полета.
Таблица 1
Время поиска одной опорной точки (в миллисекундах)
|
Высота полета, м |
Размер масок вейвлетов Габора, пикс. |
|||||
|
7×7 |
11×11 |
15×15 |
19×19 |
23×23 |
27×27 |
|
|
300 |
27–56 |
22–57 |
29–60 |
32–65 |
38–93 |
42–99 |
|
500 |
14–38 |
12–31 |
18–35 |
19–39 |
23–44 |
28–57 |
|
1000 |
10–43 |
8–38 |
12–45 |
14–46 |
19–51 |
22–59 |
|
1200 |
11–47 |
12–52 |
14–53 |
19–66 |
19–93 |
23–86 |
|
1500 |
17–79 |
14–78 |
18–92 |
23–91 |
24–91 |
28–93 |
|
2000 |
9–27 |
9–25 |
10–29 |
14–31 |
15–38 |
23–45 |
|
2500 |
10–54 |
9–44 |
14–51 |
18–51 |
19–63 |
22–90 |
Таблица 2
Погрешность в определении координат опорной точки (в пикселях)
|
Высота полета, м |
Размер масок вейвлетов Габора, пикс. |
|||||
|
7×7 |
11×11 |
15×15 |
19×19 |
23×23 |
27×27 |
|
|
300 |
X |
0,08–21,78 |
0,08–2,64 |
0,15–1,82 |
0,16–1,82 |
0,08–1,76 |
|
500 |
X |
0,06–2,05 |
0,12–1,92 |
0,15–2,02 |
0,13–1,97 |
0,03–1,98 |
|
1000 |
X |
0,13–30,24 |
0,13–1,29 |
0,06–1,11 |
0,09–1,11 |
0,03–1,12 |
|
1200 |
X |
0,07–28,78 |
0,05–0,98 |
0,07–0,99 |
0,07–0,99 |
0,05–0,95 |
|
1500 |
X |
0,05–20,62 |
0,07–0,83 |
0,09–0,87 |
0,13–0,86 |
0,11–1,04 |
|
2000 |
X |
0,13–19,25 |
0,20–1,24 |
0,12–1,08 |
0,05–1,36 |
0,15–1,24 |
|
2500 |
X |
0,05–26,17 |
0,06–15,96 |
0,09–0,97 |
0,09–1,24 |
0,09–1,23 |
Таблица 3
Максимальная погрешность в определении положения БПЛА (в метрах)
|
Высота полета, м |
Размер масок вейвлетов Габора, пикс. |
|||||
|
7×7 |
11×11 |
15×15 |
19×19 |
23×23 |
27×27 |
|
|
300 |
X |
1,07 |
0,59 |
0,43 |
0,45 |
0,41 |
|
500 |
X |
0,75 |
0,60 |
0,68 |
0,62 |
0,60 |
|
1000 |
X |
14,58 |
1,37 |
1,22 |
1,27 |
1,28 |
|
1200 |
X |
6,93 |
0,90 |
0,93 |
1,30 |
0,98 |
|
1500 |
X |
11,23 |
1,20 |
1,45 |
1,43 |
1,85 |
|
2000 |
X |
13,86 |
1,46 |
2,63 |
3,67 |
2,86 |
|
2500 |
X |
9,35 |
9,35 |
2,77 |
2,24 |
2,42 |
Символ X означает, что задачу позиционирования в данном случае решить не удалось (слишком большие погрешности в определении координат опорных точек). Результаты экспериментов показали, что маски небольшого размера не позволяют точно локализовать опорные точки. С увеличением размеров используемых масок увеличивается время поиска опорных точек, но и повышается точность их локализации. С увеличением высоты полета понижается точность позиционирования.
Максимальная погрешность в определении положения БПЛА – не более 4 метров, что превосходит точность спутниковых систем навигации. Вычисляются не только координаты БПЛА, но и углы ориентации. Максимальная ошибка в определении углов тангажа и крена составила 0,01°, в определении угла рысканья – 0,2°. Оптимальные размеры масок для фильтров по результатам экспериментов (по критерию «время/точность») – 19×19. В среднем процесс поиска 10 опорных точек на отдельно взятом видеокадре в совокупности с решением задачи внешней калибровки камеры занимал от 200 до 500 миллисекунд.
Тестирование проводилось на сгенерированных видеорядах, и снимки с реальных БПЛА могли отличаться от спутниковых из-за разницы во времени суток, времени года, климатических условиях. В работе [8] описана система визуальной навигации для полетов над плоской местностью, в которой эталонные снимки и снимки с борта БПЛА ощутимо отличались друг от друга. Для сравнения снимков использовался алгоритм SIFT, который основан на математической базе, схожей с алгоритмом SURF. Поэтому предполагается, что на реальных данных предложенная методика визуальной навигации покажет хорошие результаты.
Выводы
Результаты экспериментов показали, что фильтры (вейвлеты) Габора могут быть успешно использованы в задаче поиска точечных объектов на изображениях: в частности, в задаче навигации БПЛА с использованием видеокамеры. Использование информации о положении и ориентации БПЛА в предыдущий момент времени и максимально возможной скорости полета сокращает объем требуемых вычислений. Ректификация кадров с борта БПЛА (с применением фундаментальной матрицы, связывающей координаты особых точек с БПЛА и ИСЗ) позволяет применять фильтры Габора даже при значительных геометрических расхождениях между снимками с ИСЗ и БПЛА.
В ближайшее время планируется провести следующие исследования:
- Оптимизировать количество используемых вейвлетов Габора с целью сокращения времени поиска.
- Применить различные метрики для вычисления расстояния между джетами.
- Повысить точность локализации опорных точек с использованием субпиксельного анализа.
- Применить преобразования Фурье для вычисления откликов вейвлетов Габора.
Библиографическая ссылка
Степанов Д.Н. ПРИМЕНЕНИЕ ВЕЙВЛЕТОВ ГАБОРА В ЗАДАЧЕ НАВИГАЦИИ БПЛА С ИСПОЛЬЗОВАНИЕМ ВИДЕОКАМЕРЫ // Фундаментальные исследования. 2015. № 12-1. С. 85-91;URL: https://fundamental-research.ru/ru/article/view?id=39370 (дата обращения: 30.01.2026).



