В процессе передачи и преобразования двумерные сигналы подвергаются воздействию различных помех, что в ряде случаев приводит к ухудшению визуального качества и потере участков изображений. Оценивание истинных значений пикселей в той или иной степени необходимо в большинстве задач цифровой обработки изображений. Методы реконструкции двумерных сигналов находят свое применение в задачах обработки архивных документов в виде изображений, имеющих различные искажения (например: царапины, пятна, пыль, ненужные надписи, линии сгиба).
Большинство методов реконструкции изображений можно условно разделить на следующие группы: методы на основе решения дифференциальных уравнений в частных производных (PDE) [1]; методы на основе ортогональных преобразований [2]; методы на основе синтеза текстуры [3–4].
Использование известных методов реконструкции статических двумерных сигналов требует значительной априорной информации, уменьшение которой существенно усложняет процесс обработки изображений и в ряде случаев делает обязательным визуальный контроль и использование экспертных оценок. Неспособность восстанавливать текстуру изображений и изогнутые контуры ограничивает область использования известных методов, которые в основном применимы при удалении царапин и небольших дефектов на структуре изображений.
Целью данной работы является повышение точности реконструкции изображений на основе текстурно-геометрической модели.
Математическая модель
При реконструкции важным этапом является выбор модели изображения, от которого зависят все последующие этапы восстановления. В общем случае любое изображение по локальным геометрическим особенностям можно разделить на несколько областей – текстура и контуры. На изображении присутствуют текстурные, в том числе однородные области, разделенные границами, которые могут иметь толщину несколько пикселей и иметь различную пространственную конфигурацию. На рис. 1 представлена модель изображения, схематично представленная в виде трех подобластей.
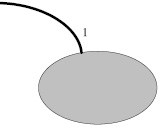
Рис. 1. Модель изображения
На основе предложенной текстурно-геометрической математической модели двумерных сигналов разработан метод синтеза неоднородного двумерного сигнала. Подход заключается в разбиении изображения на кластеры, при этом в пределах каждого предполагается однородность модели. Для восстановления границ раздела текстур предлагается использовать сплайн-интерполяцию. После восстановления границ кластеров используется операция заполнения (аппликация) этих кластеров выборочными фрагментами СП.
Метод восстановления изображений
Предлагаемый подход к реконструкции двумерных сигналов на основе текстурно-геометрической модели включает в себя четыре главных этапа:
1) нахождение фрагментов границ, пересекающих область R (на примере рис. 2, кривые ?1, ?2, ?3 и ?4);
2) определение соответствия между участками кривых;
3) интерполяция кривых, описывающих границы объектов и текстурных участков;
4) синтез текстурных областей в пределах восстановленных контуров.
Извлечение контуров объектов на изображении является нетривиальной задачей. В простейшем случае для этого может быть использован детектор Канни, который позволяет объединять в границы пиксели, для которых в направлении вектора градиента достигается локальный максимум. Недостатком такого подхода является некачественная сегментация текстур.
Для эффективной обработки предлагается использовать метод сегментации изображений на основе геометрической модели активного контура, который разработан Chan и Vese в [5]. Этот подход позволяет успешно сегментировать изображения различных типов, в том числе те, которые трудно или невозможно сегментировать классической пороговой обработкой или методами, основанными на градиенте.
Модель Chan – Vese (CV) является альтернативным решением проблемы Mumford – Shah, которая решает задачу минимизации путем минимизации следующего функционала энергии:
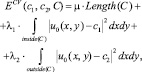
где ?, ?1 и ?2 являются положительными константами, как правило, фиксированные ?1 = ?2 = 1, c1 и c2 – средние значения интенсивности u0 внутри C и за ее пределами C соответственно.
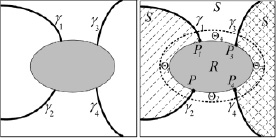
В сегментированном изображении (рис. 2, а) анализируются все участки контуров, которые находятся в локальной области ? (рис. 2, б) вокруг области R. Следующим этапом алгоритма является анализ полученных границ ?1, ?2, ..., ?k, ..., ?L и ?4, 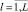 , L – количество участков границ, пересекающих область с искаженными пикселями R и их соотнесение к одной границе. Так, например, на рис. 2, б ?1, ?2 – участки первой границы ?1–2; ?3, ?4 – участки второй границы ?3–4. Cопоставление участков границ осуществляется с помощью векторного представления локальных окрестностей [6]. Локальные поверхности могут быть представлены тензором, который позволяет учитывать ориентацию изменений яркости, а также особенности изменения градиента. Для каждой локальной окрестности ?l, полученной в результате разделения области ? границами ?l и ?l+1, вычисляется тензор.
, L – количество участков границ, пересекающих область с искаженными пикселями R и их соотнесение к одной границе. Так, например, на рис. 2, б ?1, ?2 – участки первой границы ?1–2; ?3, ?4 – участки второй границы ?3–4. Cопоставление участков границ осуществляется с помощью векторного представления локальных окрестностей [6]. Локальные поверхности могут быть представлены тензором, который позволяет учитывать ориентацию изменений яркости, а также особенности изменения градиента. Для каждой локальной окрестности ?l, полученной в результате разделения области ? границами ?l и ?l+1, вычисляется тензор.
Для каждой пары точек и касательных векторов на границе ?S определяется интерполирующая кривая Эрмита. Матричная запись параметрических уравнений, описывающих элементарную кубическую кривую Эрмита, имеет вид B(t) = G?M?T,
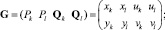
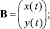

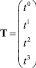 ,
,
где M – базисная матрица кубической кривой Эрмита; G – геометрическая матрица.
а б
Рис. 2. Выделение и анализ границ
Далее для каждого полученного кластера используется операция заполнения (аппликация) выборочными фрагментами СП, синтезируемых на основе различных однородных моделей, при этом полученное изображение будет обладать существенно неоднородной структурой. Одним из простейших вариантов построения модели текстур является «трёхточечная» АР модель (модель Хабиби), которая является частным случаем 2-мерной авторегрессионной модели кратности (1,1), причем значение параметра ? задает коэффициент корреляции соседних элементов:
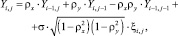
при этом первый элемент поля формируется как Y1,1 = ???1,1; первый столбец 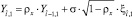 первая строка
первая строка 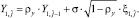
Решение системы уравнений Юла – Уокера позволяет найти коэффициенты ? уравнения авторегрессии по заданным или оцененным на основе эксперимента коэффициентам корреляции [6].
Существенным недостатком предлагаемого подхода является нерекуррентность предлагаемых процедур и, как следствие – высокие требования к вычислительным ресурсам ЭВМ.
Для увеличения быстродействия восстановление пикселей в каждой области возможно с помощью метода Телеа [7]. Использование данного подхода позволяет эффективно восстанавливать однородные области изображений с уменьшением вычислительных затрат. На рис. 3 представлен фрагмент изображения, содержащий текущую восстанавливаемую точку p.
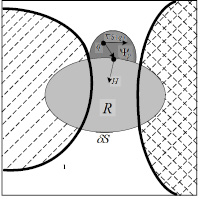
Рис. 3. Восстановление методом Телеа
Для восстановления значения пикселя p используется малая окрестность ?p в области доступных пикселей, значение которой вычисляется с учетом значений пикселей из данной окрестности и градиента изображения с использованием выражения
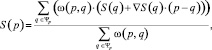
где q ? ?p – каждый пиксель из области ?p, ?(p, q) – весовая функция.
Вместо данного выражения для восстановления значений пикселей может использоваться любое другое на основе решения дифференциальных уравнений в частных производных, вычисленное в локальной области ?p. Кроме того, возможно изменение весовой функции ?(p, q). Как правило, второй и третий критерий оказывают значительное влияние только при использовании достаточно большого размера области ?p.
Оценка эффективности метода восстановления изображений
Эффективность разработанного метода проверяется на тестовых изображениях с отсутствующими пикселями, которые находятся на границах объектов. На рис. 4 представлены примеры восстановления изображений различными методами (а – исходное изображение, б – изображение с отсутствующими пикселями, в – изображение, восстановленное методом [1], г – изображение, восстановленное методом [7]; д – изображение, восстановленное методом [3]; е – изображение, восстановленное предложенным методом.



а б в



г д е
Рис. 4. Примеры восстановления изображений
Анализ результатов восстановления показывает, что предложенный метод, основанный на геометрической модели с контурным и текстурным анализом, позволяет эффективно реконструировать как текстурные, так и структурные участки изображений. Метод на основе вычисления частных производных приводит к размытию изображения, а метод на основе поиска похожих областей не корректно восстанавливает изогнутые границы.
Для численной оценки эффективности методов восстановления изображений вычисляется значение среднеквадратической ошибки
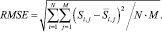
В таблице представлены усредненные значения 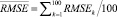 для исследуемых методов. Разработанный метод пространственной реконструкции статических изображений на основе текстурно-геометрической модели изображений позволяет уменьшить погрешность реконструкции изображений в среднем на 90 % в сравнении с известными методами.
для исследуемых методов. Разработанный метод пространственной реконструкции статических изображений на основе текстурно-геометрической модели изображений позволяет уменьшить погрешность реконструкции изображений в среднем на 90 % в сравнении с известными методами.
Значение среднеквадратической ошибки
|
|
|||
|
Метод [1] |
Метод [7] |
Метод [3] |
Предложенный метод |
|
0,1239 |
0,1232 |
0,1014 |
0,0654 |
Заключение
В статье представлен метод пространственной реконструкции статических изображений на основе текстурно-геометрической модели изображений, который заключается в реконструкции изображений с помощью восстановления контуров и синтеза текстуры путем моделирования авторегрессионной модели случайных полей. Продемонстрировано, что предлагаемый подход позволяет уменьшить ошибку восстановления при реконструкции структуры и текстуры изображений.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 15-01-09092\15.
Библиографическая ссылка
Воронин В.В., Семенищев Е.А., Франц В.А., Свирин И.С. ВОССТАНОВЛЕНИЕ ИСКАЖЕННЫХ ПИКСЕЛЕЙ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ТЕКСТУРНО-ГЕОМЕТРИЧЕСКОЙ МОДЕЛИ // Фундаментальные исследования. 2015. № 12-1. С. 17-21;URL: https://fundamental-research.ru/ru/article/view?id=39357 (дата обращения: 31.01.2026).