Процесс ректификации занимает доминирующую позицию среди всех процессов промышленного разделения, но при этом остается одним из самых энергоемких. Одним из возможных способов снижения затрат является использование периодических (циклических) режимов движения фаз в аппарате. Интерес к исследованию циклических режимов процесса ректификации обусловлен значительным повышением эффективности процесса разделения в этих режимах. Целью данной работы является анализ публикаций по исследованию указанных режимов на математических моделях и их практической реализации для выбора математической модели в дальнейших исследованиях по интенсификации циклических режимов.
Основы циклических режимов процесса ректификации
Процесс циклической ректификации основан на поочередном изменении двух режимов [3]: периода пропускания пара, в котором происходит движение парового потока вверх по колонне, и периода спуска жидкости, в котором идет подача питающей смеси, подача флегмы, а также стекание жидкости с каждой тарелки на низлежащую.
В работах, посвященных исследованию циклической ректификации [9], отмечается ряд положительных эффектов: повышение средней движущей силы процесса вследствие увеличения разности концентраций на ступенях контакта; снижение необратимых термодинамических потерь; предотвращение застойных зон; увеличения степени обновления поверхности межфазного контакта.
Развитие исследований по циклическим режимам процесса ректификации
Интерес к интенсификации процесса массообмена за счет периодических изменений режимных параметров появился в 60–70-е годы 20-го столетия. Одной из первых работ (1961 г.) по данной тематике была работа Кэннона по изучению управляемой циклической ректификации в существующих колонах с различными типами тарелок [9]. Авторам удалось достичь увеличения паровой нагрузки на 48 % при неизменном перепаде давления без внесения конструкционных изменений в колонну.
Соммерфильд и Чиен [12] в 1966 году одними из первых осуществили компьютерное моделирование процессов ректификации в циклическом и традиционном режимах, а также представили аналитическое решение дифференциальных уравнений, описывающих переходной режим. Теоретический анализ Робинсона и Энджела [10] показал преимущества циклических массообменных процессов, в которых фазы перемещаются поочередно и в любой момент времени движется только одна из фаз.
В 1967 г. Шродт [11] выполнил масштабный эксперимент по изучению управляемой циклической ректификации, для которого была спроектирована и собрана колонна диаметром 305 мм с 15 перфорированными тарелками. В циклическом режиме пропускная способность установки оказалась в два раза выше по сравнению с традиционной ректификацией при одинаковой степени разделения. В 1976 г. Гельперин [5] представил похожее исследование циклического режима на колонне с колпачковыми тарелками.
В 1980–1981 гг. Бэйрон [4] описал скачкообразную периодическую ректификацию – новый способ периодического управления, в котором потоки жидкости управлялись посредством пульсации парового потока. Теория скачкообразной периодической ректификации с некоторыми допущениями аналогична теории циклической ректификации. Эффективность колонны в обоих режимах управления одинакова при большом количестве тарелок.
В 1985 г. Фёзер и Томсон [14] представили гидродинамическую модель и результаты проверочного эксперимента на тарельчатой колонне периодического циклического действия. Фёзер и Сёни [13] продвинулись в изучении циклической ректификации, представив новый тип тарелки, представляющей традиционную ситчатую тарелку со специальным наклонным участком для снижения задержки слива жидкости.
Матсубара [8] в своем исследовании объединил схемы Кэннона [9] и Бейрона [4]. Превосходство полученной схемы было доказано с помощью математического моделирования, которое показало снижение необходимого для разделения потока пара на 20–50 %.
Интерес к циклическим режимам за последние пять лет возрос. Антон Кисс в своих исследованиях [6, 7] описал модель ректификации с попеременным движением фаз. Авторы предложили специальные клапанные контактные устройства (тарелки Малета), обеспечивающие идеальное стекание жидкости на низлежащую тарелку. Пилотные испытания показали снижение паровой нагрузки на 30 % при сохранении неизменной чистоты продуктов.
Описание математической модели
Для исследования циклического режима нами использована модель поочерёдного движения потоков пара и жидкости в колонне непрерывной ректификации бинарной смеси [1]. Соответственно время цикла τ включает время пропускания пара γτ и время спуска жидкости (1 – γ)τ.
Эффективность работы ректификационной колонны оценивалась с помощью термодинамического критерия разделительной способности колонны ξ, учитывающего характеристики входящего потока и обоих выходящих потоков [2]:
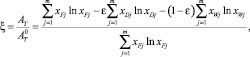(1)
где АТ – работа, необходимая для разделения смеси состава xFj на потоки дистиллята состава xDj и кубового остатка состава xWj;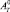 
– работа, необходимая для разделения аналогичной смеси на чистые продукты; m – число компонентов смеси; ε – доля отбора с дистиллятом.
Согласно введенному критерию, качество разделения считается тем выше, чем больше требуется затратить для его достижения работоспособной энергии при идеальном ведении процесса. Это соответствует максимальному значению критерия ξ.
Допущения в принятой модели:
– изменение концентрации легколетучего компонента (ЛЛК) в паре, покидающем тарелку, мгновенно следует за изменением концентрации жидкости на тарелке;
– имеет место эквимолярный массообмен;
– количество жидкости на тарелках одинаково на всех ступенях одной секции;
– величина КПД по Мэрфри постоянна на данной ступени разделения;
– разделяется бинарная смесь, поступающая в колонну в жидком виде при температуре кипения;
– уносом жидкости можно пренебречь;
– в период движения пара на всех тарелках имеет место идеальное смешение;
– конденсатор колонны полный;
– концентрация пара, покидающего куб, равна концентрации кубовой жидкости;
– флегма и питание поступают в колонну циклично;
– за период движения жидкости со всех ступеней одной секции стекают постоянные и равные количества жидкости;
– за период движения жидкости массообмен отсутствует.
При пропускании пара процесс массообмена на тарелке описывается уравнением
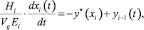(2)
где Hi – объём жидкости на ступени разделения i; Vg – расход пара по колонне; Ei – КПД по Мерфри на ступени разделения i; xi – содержание ЛЛК в жидкости на тарелке i; yi – содержание ЛЛК в паре на тарелке i; y*(xi) – равновесное содержание ЛЛК в паре на тарелке i.
Дефлегматор и куб в период пропускания пара описываются дифференциальными уравнениями, соответственно
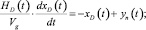(3)
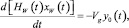(4)
где HD и HW – объёмы жидкости в дефлегматоре и в кубе.
При спуске жидкости в блоке перемешивания на тарелке процесс описывается уравнением
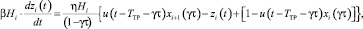(5)
где β – коэффициент межтарельчатого перемешивания; zi – концентрация ЛЛК в блоке перемешивания на тарелке i; η – доля замены жидкости на тарелке; γ – доля периода пропускания пара; τ – период цикла; TTP – время транспортного запаздывания перемешивания жидкости на тарелке; u(t – TTP – γτ) – ступенчатая знаковая функция, принимающая значение 0 при t ≤ TTP + γτ и значение 1 при t > TTP + γτ.
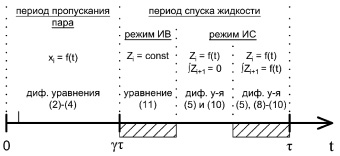
На рисунке показаны пути проведения расчета при TTP ≥ (1 – γ)τ и TTP < (1 – γ)τ.
Если время транспортного запаздывания перемешивания жидкости TTP превышает продолжительность периода спуска жидкости (рисунок, а), ступенчатая функция u(t – TTP – γτ) принимает значение 0. При этом концентрация ЛЛК на момент окончания периода при t = τ для всех тарелок, кроме питающей тарелки, описывается алгебраическим уравнением
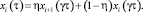(6)
Для тарелки питания i = K уравнение (6) принимает следующий вид:
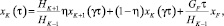(7)
где GF – расход питающей смеси; xF – содержание ЛЛК в жидкой фазе питания.
Концентрация ЛЛК в случае, когда время транспортного запаздывания перемешивания жидкости меньше периода спуска жидкости (рисунок, б), рассчитывается по формулам
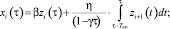(8)
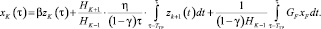(9)
При этом концентрация в блоке перемешивания для тарелки питания описывается уравнением
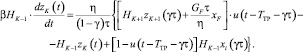(10)
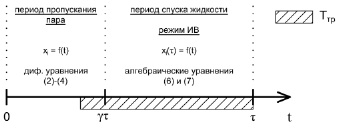
а
б
Пути проведения расчета: а – TTP ≥ (1 – γ)τ; б – TTP < (1 – γ)τ
Для γτ < t ≤ γτ + TTP решением дифференциальных уравнений (5) и (10) будет
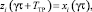(11)
т.е. за время транспортного запаздывания перемешивания жидкости при спуске жидкости не происходит изменение концентрации компонентов в блоке перемешивания.
Путь проведения расчета для одного цикла в зависимости от величины времени транспортного запаздывания перемешивания жидкости представлен на рисунке. При значении TTP меньше периода спуска жидкости расчет усложняется и возникают три системы уравнений, сменяющих друг друга. При 0,5∙(1 – γ)τ < TTP < (1 – γ)τ происходит взаимное наложение данных систем, что значительно усложняет алгоритм расчета.
Заключение
Анализ работ по исследованию эффективности циклических режимов процесса ректификации свидетельствует о целесообразности дальнейшего исследования форм и области применения циклических режимов ректификационных колонн в зависимости от задач их функционирования, особенностей разделяемых смесей. Для продолжения исследований циклических режимов процесса ректификации в указанных направлениях нами ведутся работы по их программному обеспечению и определению оптимальных параметров.
Рецензенты:
Дыда А.А., д.т.н., профессор кафедры автоматических информационных систем, Морской государственный университет им. адм. Г.И. Невельского, г. Владивосток;
Кондриков Н.Б., д.х.н., профессор, зав. кафедрой физической и аналитической химии Школы естественных наук, Дальневосточный федеральный университет, г. Владивосток.
Библиографическая ссылка
Кривошеев В.П., Ануфриев А.В. ОСНОВЫ И ЭФФЕКТИВНОСТЬ ЦИКЛИЧЕСКИХ РЕЖИМОВ ПРОЦЕССА РЕКТИФИКАЦИИ // Фундаментальные исследования. – 2015. – № 11-2. – С. 267-271;URL: https://fundamental-research.ru/ru/article/view?id=39322 (дата обращения: 19.04.2024).