Как показали многочисленные исследования электронных средств измерений, дрейф метрологических характеристик из-за влияющих факторов в общем случае может быть представлен как нелинейное преобразование данных метрологических характеристик во времени. Среди нелинейных преобразований можно выделить два класса [1]: безынерционные (функциональные) и инерционные. Наиболее характерными для автономных средств измерений являются нелинейные инерционные преобразования. При таких преобразованиях изменения метрологических характеристик описываются нелинейным дифференциальным уравнением.
Существуют три основных метода решения нелинейных стохастических дифференциальных уравнений [1, 2]: с помощью уравнения Фоккера – Планка – Колмогорова, квазилинейный метод и метод функциональных рядов.
Цель работы – анализ методов уравнения Фоккера – Планка – Колмогорова, квазилинейного метода и метода функциональных рядов на конкретном примере.
Уравнение Фоккера – Планка – Колмогорова
Рассмотрим нелинейную инерционную систему второго порядка, которая описывается следующим нелинейным стохастическим дифференциальным уравнением:
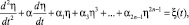 (1)
(1)
где a и ai – постоянные коэффициенты; n – положительное целое число; ξ(t) – гауссовский белый шум с нулевым математическим ожиданием и дельтаобразной корреляционной функцией
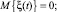
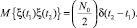 (2)
(2)
Перейдём в уравнении (1) к новым переменным: λ1 = η, λ1 = dη/dt. Тогда вместо дифференциального уравнения второго порядка получим систему из двух дифференциальных уравнений первого порядка
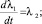
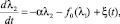
где
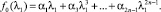 (3)
(3)
Двухкомпонентный процесс {λ1(t), λ2(t)} является непрерывнозначным диффузионным марковским процессом. Вычислив по обычным правилам функции сноса и диффузии, для одномерной плотности вероятности p(λ1, λ2, t) можем записать уравнение ФПК
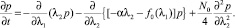 (4)
(4)
Допустим, что нелинейная функция f0(λ1) такова, что при t → ∞ система стремится к стационарному состоянию. Положив 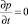 , для стационарной плотности вероятности pst(λ1, λ2) из (4) получим уравнение
, для стационарной плотности вероятности pst(λ1, λ2) из (4) получим уравнение
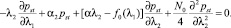 (5)
(5)
Будем искать решение этого уравнения в виде произведения двух функций:
pst(λ1, λ2) = g(λ1)h(λ2). (6)
Подставив (6) в (5) и расщепив переменные, для определения функций g и h получим систему дифференциальных уравнений
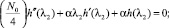
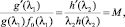
где штрихами обозначены производные. Из второго уравнения находим 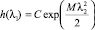 . Подстановка этого выражения в первое дифференциальное уравнение даёт M = –4α/N0. Поэтому
. Подстановка этого выражения в первое дифференциальное уравнение даёт M = –4α/N0. Поэтому
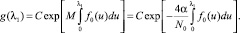 (7)
(7)
Так как, λ1 = η, то из (7) получаем интересующую нас одномерную плотность вероятности выходного процесса h(t)
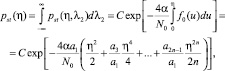 (8)
(8)
где постоянная С находится из условия нормировки плотности вероятности.
В частном случае, когда a1 > 0, a3 > 0, a5 = … = a2n–1 = 0, плотность вероятности принимает вид
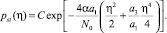 (9)
(9)
Воспользовавшись известным интегралом
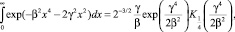
где Kv(z) – цилиндрическая функция мнимого аргумента, получим
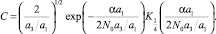 (10)
(10)
Так как плотность вероятности является частной функцией, то все нечетные моменты выходного процесса η(t) равны нулю, а дисперсия может быть определена по формуле
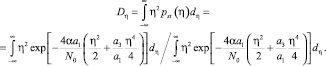 (11)
(11)
Зависимость дисперсии Dη от 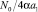 для нескольких значений параметра
для нескольких значений параметра 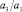 , полученная численным интегрированием, воспроизведена на рис. 1 (непрерывные кривые).
, полученная численным интегрированием, воспроизведена на рис. 1 (непрерывные кривые).
Квазилинейный метод и метод функциональных рядов
Идея этого метода, называемого также методом статистической линеаризации [2, 3, 4, 5, 6, 7, 8, 9], состоит в нахождении наилучшей (в определенном смысле) замены нелинейной системы линейной. В общем случае затруднительно линеаризовать зависимость выходного процесса от входного воздействия. Однако при наличии в системе безынерционных нелинейных элементов можно искусственно произвести линеаризацию только этих элементов, оставив без изменения линейную часть. При этом получается простая линейная система.
Пусть зависимость выходного процесса ζ(t) безынерционной нелинейности от входного η(t) имеет вид ζ(t) = f(η(t)). В квазистатическом методе функция ζ = f(η) заменяется линейной
ζ = k0 + kη,
где k – так называемый эквивалентный коэффициент усиления. Выбирая тот или иной критерий линеаризации, можно определить коэффициенты k0 и k.
Если принять критерий минимума среднего квадрата ошибки
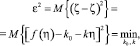 (12)
(12)
то для определения коэффициентов k0 и k получим систему двух алгебраических уравнений
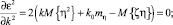
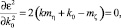
где
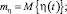
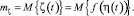
Отсюда
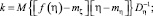
k0 = mζ – kmη. (13)
Для определения коэффициентов k0 и k по этим формулам необходимо знать вероятностные характеристики выходного процесса η(t). Однако они пока неизвестны и должны быть получены в результате решения задачи. Поэтому излагаемый квазилинейный метод нельзя признать логически безупречным и достаточно обоснованным. Часто при нахождении коэффициентов k0 и k формально полагают, что плотность вероятности выходного процесса η(t) является нормальной (хотя, например, формула (13) свидетельствует, что это не так).
В рассматриваемом примере входной белый шум ξ(t) имеет нулевое математическое ожидание и нелинейность нечетная. Поэтому математические ожидания процессов η(t) и ζ(t) = f(η(t)) будут равны нулю и формулы (13) упрощаются:
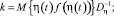 k0 = 0. (14)
k0 = 0. (14)
Если формально принято, что процесс η(t) имеет нормальное распределение с нулевым математическим ожиданием и дисперсией Dη, то для нелинейности
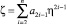 (15)
(15)
эквивалентный коэффициент усиления будет равен
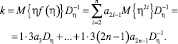 (16)
(16)
Здесь последнее равенство написано на основании известной формулы для четных моментов нормального распределения:
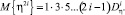 (17)
(17)
Возвратимся теперь к исходному дифференциальному уравнению (6). Сущность квазилинейного метода состоит в том, что в уравнении (6) полином a3η3 + ... + a2n–1η2n–1 заменяется линейной функцией kη, что соответствует переходу от исходной нелинейной системы к линейной системе. Линеаризованная система имеет комплексную частотную характеристику
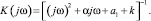 (18)
(18)
Спектральная плотность выходного процесса η(t) в стационарном состоянии определяется известной формулой
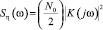 . (19)
. (19)
По спектральной плотности находим дисперсию
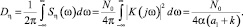 (20)
(20)
Подставив сюда k из (16), получим
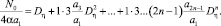 (21)
(21)
На рисунке приведена зависимость Dη от 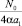 при нескольких значениях параметра
при нескольких значениях параметра 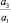 для случая, когда a5 = ... = a2n–1 = 0 (штриховые кривые).
для случая, когда a5 = ... = a2n–1 = 0 (штриховые кривые).
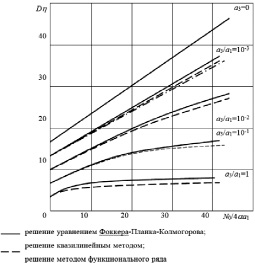
Решения уравнения
Квазилинейный метод сравнительно прост и для рассмотренного примера дает хорошие результаты. Однако приводимое сравнение методов только по точности определения дисперсии (а не других характеристик) не является показательным согласно принятому критерию нахождения эквивалентного коэффициента усиления. Справедливость метода теоретически не обоснована; он является эвристическим и логически непоследовательным.
Метод функциональных рядов по существу обобщает квазилинейный метод и имеет примерно ту же область применения. Он позволяет получить более точные результаты, но является весьма трудоемким. При его применении возникает дополнительная проблема — оценка сходимости ряда.
Когда выходной процесс системы можно свести к марковскому, применение уравнения Фоккера – Планка – Колмогорова позволяет получить точное решение задачи. Поэтому всегда целесообразно на основании физических соображений выходной процесс аппроксимировать марковским. Конечно, может оказаться (особенно для многомерных нелинейных систем), что получить аналитическое решение уравнения Фоккера – Планка – Колмогорова затруднительно и потребуются приближенные аналитические или численные методы решения. Однако необходимо иметь в виду, что в принципе только теория марковских процессов позволяет математически анализировать нелинейные инерционные системы с несколькими состояниями устойчивого равновесия (включая процессы захвата и срыва слежения); других методов не существует.
Рецензенты:
Звездина М.Ю., д.ф.-м.н., доцент, зав. кафедрой «Радиоэлектроника», ФГБОУ ВПО «Донской государственный технический университет», г. Ростов-на-Дону;
Габриэльян Д.Д., д.т.н., профессор, заместитель начальника научно-технического комплекса «Антенные системы» по науке, ФНПЦ ФГУП «Ростовский научно-исследовательский институт радиосвязи», г. Ростов-на-Дону.
Библиографическая ссылка
Безуглов Д.А., Юхнов В.И. НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК АВТОНОМНЫХ СРЕДСТВ ИЗМЕРЕНИЙ // Фундаментальные исследования. 2015. № 11-2. С. 232-236;URL: https://fundamental-research.ru/ru/article/view?id=39316 (дата обращения: 20.02.2026).



