В данной статье описан алгоритм моделирования циклических режимов процесса бинарной ректификации. Он включает последовательность расчёта концентраций легколетучего компонента на каждой из тарелок колонны бинарной ректификации в циклических режимах для следующих случаев:
– пропускание паров через жидкость на каждой из тарелок колонны с учётом гидродинамической обстановки на тарелках, в кубе и в конденсаторе колонны;
– спуск жидкости с тарелок колонны для возможных случаев соотношения времени транспортного запаздывания перемешивания жидкости потока на тарелке и доли времени цикла спуска жидкости от времени общего цикла процесса с учётом доли замены жидкости на тарелке и коэффициента межтарельчатого перемешивания.
Известные исследования по интенсификации процесса ректификации свидетельствуют о возможности значительного повышения эффективности разделения, если обеспечить работу ректификационной колонны в циклическом режиме. При этом поочерёдно на каждой тарелке колонны с определённым периодом организуется пропускание парового потока через жидкость, находящуюся на тарелке, а затем подача пара прекращается и жидкость спускается на нижележащую тарелку.
Объектом исследования в данной работе выбрана лабораторная ректификационная установка Didacta IC18DV/92 [5] диаметром 60 мм, содержащая 11 колпачковых тарелок с высотой слива 30 мм. Рассматривалось разделение смеси этанол – вода при атмосферном давлении. Питание подавалось на 6 тарелку при температуре кипения смеси.
Целью данной работы является описание алгоритма расчета циклического режима процесса бинарной ректификации, рассмотрение особенностей алгоритма и представление примеров расчета для отдельной тарелки объекта исследования.
Краткое описание математической модели
Для исследования циклического режима нами использована модель поочерёдного движения потоков пара и жидкости в колонне непрерывной ректификации бинарной смеси [2]. Время цикла τ включает время пропускания пара γτ и время спуска жидкости (1 – γ)τ. Основные уравнения, описывающие переходные процессы на тарелке, представлены ниже.
При пропускании пара процесс массообмена на тарелке описывается уравнением
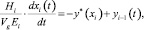(1)
где Hi – объём жидкости на ступени разделения i; Vg – расход пара по колонне; Ei – КПД по Мерфри на ступени разделения i; xi – содержание легкокипящего компонента (ЛЛК) в жидкости на тарелке i; yi – содержание ЛЛК в паре на тарелке i; y*(xi) – равновесное содержание ЛЛК в паре на тарелке i.
При спуске жидкости в блоке перемешивания на тарелке процесс описывается уравнением
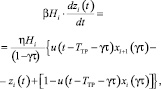(2)
где β – коэффициент межтарельчатого перемешивания; zi – концентрация ЛЛК в блоке перемешивания на тарелке i; η – доля замены жидкости на тарелке; γ – доля периода пропускания пара; τ – период цикла; TTP – время транспортного запаздывания перемешивания жидкости на тарелке; u(t – TTP – γτ) – ступенчатая знаковая функция, принимающая значение 0 при t ≤ TTP + γτ и значение 1 при t > TTP + γτ.
Если время транспортного запаздывания перемешивания жидкости TTP превышает продолжительность периода спуска жидкости, ступенчатая функция u(t – TTP – γτ) принимает значение 0. При этом концентрация ЛЛК на момент окончания периода при t = τ для всех тарелок, кроме питающей тарелки, описывается алгебраическим уравнением
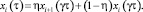(3)
Концентрация ЛЛК в случае, когда время транспортного запаздывания перемешивания жидкости меньше периода спуска жидкости, рассчитывается по формуле
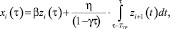(4)
Для γτ < t ≤ γτ + TTP решением дифференциального уравнения (2) будет
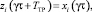(5)
т.е. за время транспортного запаздывания перемешивания жидкости при спуске жидкости не происходит изменение концентрации компонентов в блоке перемешивания.
Алгоритм моделирования циклических режимов процесса бинарной ректификации
Блок-схема общего алгоритма расчета представлена на рис. 1. В качестве исходных данных используются параметры состояния исходного статического режима (расходы питания GF и пара VD, состав питания XF, флегмовое число R, КПД тарелки по Мерфри E, профиль концентрации ЛЛК в жидкости по колонне xi) и требуемые параметры циклического режима (период цикла τ, доля периода пропускания пара γ, доля замены жидкости на тарелке η, коэффициент межтарельчатого перемешивания β).
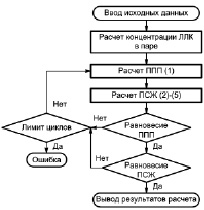
Рис. 1. Общий алгоритм расчёта циклического режима
На основании данных статического режима о содержании ЛЛК в жидкости рассчитывается профиль концентрации ЛЛК в паре для каждой тарелки yi.
Уравнение (1) при расчете на каждой ступени разделения в период пропускания пара (ППП) решается численно. В данной работе использован метод Рунге – Кутты четвертого порядка (в дальнейшем метод РК4) с суммарной ошибкой на конечном интервале интегрирования порядка h4 [4]. На каждом шаге итерации метода РК4 расчет xi необходимо начинать с нижней ступени разделения при i = 0, так как согласно принятому в модели допущению переменная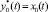 
[1]. В этом случае решение данной системы уравнений с использованием условий парожидкостного равновесия не представляет трудностей.
Блок-схема алгоритма расчета процесса в период спуска жидкости (ПСЖ) показана на рис. 2. В зависимости от соотношения времени транспортного запаздывания перемешивания жидкости и времени периода спуска жидкости концентрация xi рассчитывается по уравнению (3) (случай А) или по уравнению (4) (случай Б). Для случая Б необходимо также учитывать две особенности:
– zi = const для промежутка времени t от γτ до γτ + TTP согласно уравнению (5);
– для расчета xi, согласно уравнению (4), необходимо знать общее количество ЛЛК, прошедшего с верхней тарелки за промежуток времени от τ – TTP до τ.
Если время спуска жидкости мало и превышает время транспортного запаздывания перемешивания жидкости (случай А), расчет xi для ППП ведется сразу для момента времени τ по алгебраическому уравнению (3). В этом случае при пропускании пара концентрация ЛЛК в жидкости на тарелке постепенно снижается, а в период спуска жидкости скачкообразно возрастает.
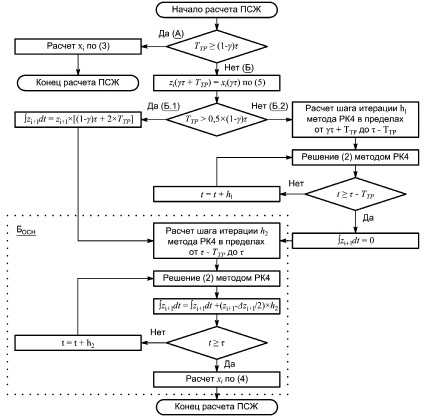
Рис. 2. Алгоритм расчета ПСЖ
Процесс расчета содержания этанола для случая А на примере двух ППП и одного ПСЖ на 7-й тарелке 11-тарельчатой колонны разделения водно-этаноловой смеси графически показан на рис. 3, А (время цикла – 10 с; время спуска жидкости – 5 с; время транспортного запаздывания перемешивания жидкости 7 с; количество шагов итерации метода РК4-10). В процессе расчета на основании исходной концентрации ЛЛК на тарелке (0,364 доли) вычисляются методом РК4 точки, соответствующие ППП. Концентрация этанола на тарелке к концу ППП (t = 5,0 c) составила 0,319. ТТР превышает время спуска жидкости, поэтому стекание жидкости происходит в поршневом режиме. Содержание этанола скачкообразно возрастает, и концентрация этанола (0,371) высчитывается сразу для времени 10 с.
Если время спуска жидкости превышает время транспортного запаздывания перемешивания жидкости (случай Б), то необходимо решать совместно уравнения (2), (4) и (5). На первом этапе, согласно уравнению (5), принимаем концентрацию ЛЛК в блоке перемешивания в момент γτ + TTP равной концентрации на тарелке. Дальнейший путь расчета зависит от величины ТТР. Возможные варианты расчета Б.1 и Б.2 представлены на рис. 4.
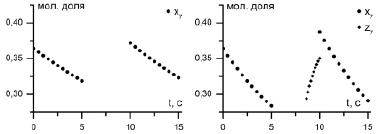
А Б
Рис. 3. Расчетное изменение во времени концентрации этанола на 7-й тарелке: а – τ = 10,0 с; γ = 0,5; ТТР = 7,0 с; б – τ = 10,0 с; γ = 0,5; ТТР = 3,5 с
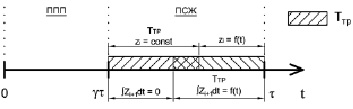
Б1
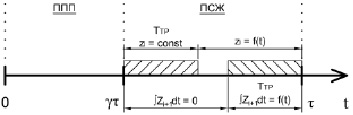
Б2
Рис. 4. Влияние величины ТТР на вычисления интеграла в уравнении (4)
Согласно уравнению (4), для расчета xi в момент окончания ПСЖ необходимо вычислить интеграл в пределах от τ – TTP до τ. При ТТР > 0,5∙(1 – γ)τ оставшееся после исключения ТТР время спуска жидкости меньше предела интегрирования, и для вычисления недостающей части интеграла необходимо производить дополнительные расчеты (случай Б.1) с последующим обращением к блоку БОСН (рис. 1).
Блок БОСН описывает решение дифференциального уравнения (2) методом РК4 для каждой ступени разделения. На каждом шаге итерации метода РК4 к текущему значению интеграла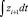 
прибавляют произведение среднего значения zi + 1 на величину шага по времени в этой итерации h2. При достижении времени окончания ПСЖ производят расчет xi для каждой ступени разделения по уравнению (4). В период спуска жидкости концентрация ЛЛК в блоке перемешивания остается неизменной за время TTP, пока идет идеальное вытеснение, а затем идёт увеличение концентрации в блоке перемешивания (рис. 3Б).
Процесс расчета содержания этанола на 7-й тарелке той же колонны описан далее для случая Б.1 и графически показан на рис. 3, Б. Для тех же параметров работы колонны, кроме величины транспортного запаздывания перемешивания жидкости (3,5 с), процесс расчета ППП аналогичен. Изменение конечной концентрации этанола по сравнению с предыдущим случаем связано с изменением объема жидкости на тарелках, которое вызвало изменение TTP. В диапазон времени от 5 до 8,5 с (за время ТТР) в ПСЖ zi остается постоянной и не вычисляется. В период времени 8,5–10 с изменение zi рассчитывается методом РК4. Затем рассчитывается xi (для t = 10 с) по уравнению (4) с использованием значения zi (для t = 10 с) и интеграла в пределах от 6,5 с до 10 с, причем часть интеграла в пределах от 6,5–8,5 с рассчитывается по выражению
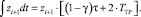
При ТТР ≤ 0,5∙(1 – γ)τ необходимо произвести расчет zi по уравнению (2) методом РК4 аналогично блоку БОСН в пределах γτ + TTP до τ – ТТР (случай Б.2). При этом значение интеграла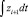 
остаётся равным нулю. По окончанию расчета уравнения (5) выполняется переход к вычислению блока БОСН аналогично случаю Б.1. В период спуска жидкости изменение концентрации ЛЛК в блоке перемешивания аналогично случаю Б.1 (рис. 3, б).
Алгоритм расчета циклического режима реализован в программном продукте [3].
Заключение
В предлагаемом алгоритме учтены возможные случаи соотношений времени спуска жидкости со временем транспортного запаздывания жидкости на тарелке. Предлагаются вычислительные процедуры, обеспечивающие сходимость расчёта циклического режима и приводится иллюстрация результатов моделирования при исходных данных с лабораторной тарельчатой ректификационной установки.
Рецензенты:
Дыда А.А., д.т.н., профессор кафедры автоматических информационных систем, Морской государственный университет им. адм. Г.И. Невельского, г. Владивосток;
Кондриков Н.Б., д.х.н., профессор, зав. кафедрой физической и аналитической химии Школы естественных наук, Дальневосточный федеральный университет, г. Владивосток.
Библиографическая ссылка
Ануфриев А.В., Кривошеев В.П. МОДЕЛИРОВАНИЕ ЦИКЛИЧЕСКИХ РЕЖИМОВ ПРОЦЕССА БИНАРНОЙ РЕКТИФИКАЦИИ // Фундаментальные исследования. – 2015. – № 11-2. – С. 227-231;URL: https://fundamental-research.ru/ru/article/view?id=39315 (дата обращения: 23.11.2024).