Эффективность процесса смешивания сыпучих материалов в аппаратах с образованием разреженных потоков компонентов значительно повышается при использовании дополнительных отбойных элементов. Актуальная проблема оценки коэффициента неоднородности получаемой смеси может быть решена с помощью стохастического подхода [4, 7, 9] с учетом эффекта ударного взаимодействия формируемых разреженных факелов [2] с отбойной поверхностью заданной формы. Пусть установка имеет вращающийся барабан с радиально расположенными гибкими элементами при частоте вращения n, который имеет некоторый зазор с подвижной лентой. Данная лента одновременно служит транспортером – для сыпучих компонентов при их послойной подаче в указанный зазор и для готовой смеси после отражения факелов разносортных материалов от установленного под углом γ плоского отбойника (рис. 1). Условно можно выделить два вида потоков – налетающие на отбойник после «срыва » твердых частиц дисперсных компонентов с гибких лопастей вращающегося барабана и отраженные от него.
Цель работы: моделирование дифференциальных функций распределения сыпучих компонентов в рабочем объеме барабанно-ленточного смесителя с гибкими элементами, расположенными радиально на вращающихся относительно горизонтальных осей цилиндрических барабанах в зависимости от угла распыливания частиц с учетом эффекта взаимодействия формируемых потоков с плоским отбойником.
Описание распределения частиц сыпучих компонентов в зависимости от их диаметров
Базируясь на стохастическом подходе [1, 3], предлагается ввести двумерные функции распределения вероятностей
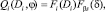i = 1, ..., r
для каждого разреженного потока частиц сыпучих компонентов по их диаметрам Di и углам отклонения δ в i факелах. Каждая из указанных функциональных зависимостей Fi(Di) и Fβs(δ) моделируется отдельно. Считается, что согласно теории ударных процессов в дисперсных системах [4] дифференциальная функция распределения для частиц i-го компонента по их диаметрам моделируется в форме
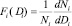(1)
для фазового пространства с элементом dΓi = dWxidDi, соответствующим совокупности одной компоненты скорости Wxi центра масс i-й сферической частицы и ее диаметра Di.
Отыскание функций вида Fi(Di) соответствует экспоненциальному убыванию числа частиц каждого из набегающих потоков для смешиваемых компонентов сыпучих материалов dNi в элементе фазового объема dΓi в зависимости от стохастической энергии частицы Ei [5, 6]
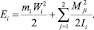(2)
Входящие в выражение (1) суммы кинетических энергий при поступательном и вращательном движениях соответствуют энергиям частиц каждого i-го потока. Дополнительно учитываются случайные моменты импульсов описанных частиц в виде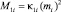 
и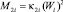 
, где обозначены: их масса mi, диаметр Di и скорость Wi. Заметим, что моменты инерции рассчитываются при вращениях частиц – после «срыва» с гибкого элемента барабана, вращающегося со скоростью n1, и за счет вторичных столкновений [8]. Константа Ai задается нормировкой 
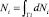. Следовательно, учитывая ρTi – истинные плотности смешиваемых компонентов и обозначения 
; 
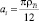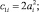с2i = 10ai, имеем
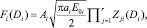(3)
где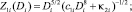 
.
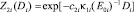Входящие в (3) параметры имеют размерности [E0i] = Дж; [κ1i] = м4с–2, [κ2i] = кг2м2 и вычисляются из системы энергетических уравнений.
В частности, E0i и κ1i – из уравнений в виде равенств – энергий потоков до столкновения со стенкой (в момент удара каждого из i разреженных исходных компонентов об отбойную поверхность), а также – при падении отраженного факела на горизонтальную ленту (рис. 1).
Рис. 1. Упрощенная схема устройства ударного действия: 1 и 2 – дозаторы; 3 и 4 – слои сыпучих материалов; 5 – лента; 6 – барабан; 7 – гибкие элементы; 8 – отбойник; 9 – дисперсная смесь
Параметр κ2i – из уравнения сохранения потоков при равенстве концентрации столкнувшихся частиц из i компонентов 
и разности между концентрациями – полного числа частиц для каждого ингредиента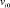 
и для общего числа частиц i сортов, не участвующих в столкновениях 
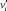, когда выполняется условие
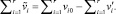
Значение 
рассчитывается для единичного объема области, в которой предполагаются возможными их взаимодействия, т.е. Zβs – зоны наиболее вероятного присутствия частиц каждого из потоков – налетающих и отраженного. Например, в качестве такой может быть выбран сектор окружности с центром в точке предполагаемого падения усредненного потока, радиусом h и углом раствора π.
Описание распределения частиц сыпучих компонентов в зависимости от угла отражения от плоского отбойника
При выборе полунормального закона для Fβs(δ) – распределения отраженных частиц по углам с учетом нормировочного множителя F0s
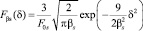(4)
наиболее вероятной областью отражения смешиваемых частиц считается часть описанного сектора для βs = β1 + β2 – суммы углов падения β1 и отражения β2 усредненных векторов перемещений потоков. Таким образом, суммы указанных концентраций 
и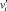 
рассчитываются с учетом коэффициента восстановления kv; концентраций числа не столкнувшихся частиц i-го налетающего потока с элементами j-го налетающего, а также – отраженного.
Формирование критерия качества смеси
Критерий качества смеси выбран в форме коэффициента неоднородности
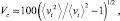(5)
когда i = 1, 2 и объемные концентрации равны
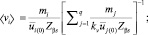(6)
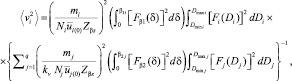(7)
где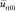 
– усредненная скорость налетающего потока; Zβs = hL/2; Zβs = πh2/2; L – расстояние между точкой касания барабана с поверхностью сыпучего компонента на ленте и точкой крепления отбойника на горизонтальной поверхности.
Входящие в выражение (7) интегральные выражения с учетом вида Fβs(δ) – распределения частиц по углам в применении соответственно к налетающему и отраженному потокам имеют вид
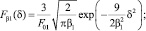(8)
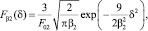(9)
где значения нормировочных параметров F01 и F02 равны
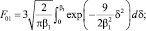(10)
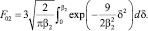(11)
Подстановка в формулу (5) для коэффициента неоднородности выражений (8), (9) для указанных распределений частиц с учетом (10), (11) приводит к следующему представлению:
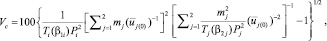(12)
где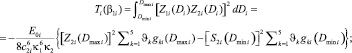 
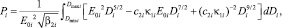
когда при ϑ1 = ϑ2 = 30, ϑ3 = 20, ϑ4 = 10, ϑ5 = 4 введены обозначения
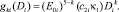
Результаты исследования и их обсуждение
Введение безразмерного параметра ε = D/Dmin2 позволяет согласно (3), (4) получить следующее представление для Qi(ε, δ) – общей функции распределения частиц по диаметрам и углам (рис. 2), применяемой в соответствии с (5)–(7) для расчета Vc (рис. 3) в зависимости от режимных параметров аппарата – частоты вращения барабана n1 и угла наклона отбойной поверхности γ. Для сравнения на рис. 4 приведем семейство кривых для qi(ε) – одномерных дифференциальных функций распределения по параметру ε.
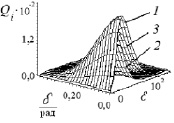
Рис. 2. Зависимости Qi(ε, δ) и Qm(ε, δ): 1 – каолин ГОСТ 21235-75 (i = 1); 2 – технический углерод П803 ГОСТ 7885-86 (i = 2); 3 – для их смеси
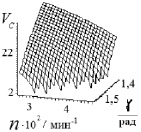
Рис. 3. Зависимость для коэффициента неоднородностей Vc(n, γ) при смешении каолина ГОСТ 21235-75 и технического углерода П803 ГОСТ 7885-86 в устройстве ударного действия
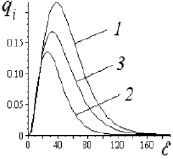
Рис. 4. Зависимости qi(ε) и qm(ε): 1 – каолин ГОСТ 21235-75 (i = 1); 2 – технический углерод П803 ГОСТ 7885-86 (i = 2); 3 – для их смеси
Пересечение диапазонов диаметров частиц для рабочих сыпучих материалов (каолина ГОСТ 21235-75 и технического углерода П803 ГОСТ 7885-86) приводит к промежуточному положению соответствующей кривой qm(ε) (кривая 3, рис. 4) или поверхности Qm(ε, δ) (поверхность 3, рис. 2) для смеси порошков. При этом наблюдается некоторое снижение значений двумерных распределений вероятностей Qi(ε, δ) и Qm(ε, δ) по сравнению с одномерными – qi(ε) и qm(ε), что объясняется наличием дополнительного перераспределения частиц описанных потоков по углу γ. Полученные распределения qi(ε) и Qi(ε, δ) позволяют различными способами оценить качество приготавливаемой смеси при выборе коэффициента неоднородностей в виде критерия (5).
Конструктивными и режимными показателями установки являются: D1 = 7,5∙10–2 м; l = 4,00∙10–2 м; L = 0,45 м; n = 300 об/мин; Wi = 10–2 м/с; α = 40°; γ = 75°. С увеличением угла наклона отбойника до значения π/2 происходит значительное улучшение качества продукта, что можно объяснить расширением условной зоны перекрещивания потоков компонентов.
Заключение
Примеры вычисления Vc по формуле (5) удовлетворительно описывают процесс смешения порошков, что подтверждается опытными данными: при n = 300 об/мин и изменении угла наклона отбойной поверхности в пределах γ = (0,54–1,72) рад экспериментальные значения имеют диапазон Vc = (19,4 – 23,2). Выражения (5)–(7) могут быть использованы при формировании инженерной методики расчета устройства ударного действия для смешивания сыпучих материалов.
Рецензенты:
Бачурин В.И., д.ф.-м.н., профессор кафедры «Высшая и прикладная математика» Ярославский филиал, ФГБОУ ВПО «Московский государственный университет путей сообщения (МИИТ)», г. Ярославль;
Мурашов А.А., д.т.н., профессор кафедры математики, Ярославское высшее военное училище противовоздушной обороны, г. Ярославль.
Библиографическая ссылка
Капранова А.Б., Верлока И.И., Лебедев А.Е. МОДЕЛИРОВАНИЕ ДВУМЕРНЫХ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ ДЛЯ ОПИСАНИЯ УДАРНОГО СМЕШИВАНИЯ СЫПУЧИХ СРЕД // Фундаментальные исследования. – 2015. – № 11-1. – С. 54-58;URL: https://fundamental-research.ru/ru/article/view?id=39283 (дата обращения: 23.11.2024).