Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Прахов И.В. 1 Бикметов А.Г. 1

---

1 Филиал ФГБОУ ВПО «Уфимский государственный нефтяной технический университет»

Применение искусственных нейронных сетей в задачах диагностики вызывает все больший интерес. Нейронные сети позволяют сократить аппарат распознавания образов без изменения достоверности результатов. Важным преимуществом использования нейронных сетей в задачах диагностики является обучаемость. Построение нейросетевой модели происходит адаптивно во время обучения без участия эксперта. При этом нейронной сети предоставляются примеры из базы данных, и она сама подстраивается под эти данные. Основной задачей теории планирования эксперимента является определение значений коэффициентов уравнений регрессии, с помощью которых определяется функциональная зависимость выходной величины от воздействующих факторов. Применение теории планирования эксперимента во время обучения искусственной нейронной сети позволяет увеличить базу данных и тем самым повысить достоверность определения технического состояния насосного оборудования с электрическим приводом.

Статья в формате PDF

471 KB

насосный агрегат

нейронная сеть

спектральный метод

обучение

повреждение

режим работы

планирование эксперимента

гармоники

реплика

фактор

1. Баширов М.Г., Прахов И.В. Исследование влияния неисправностей элементов насосно-компрессорного оборудования на параметры генерируемых двигателем электропривода высших гармонических составляющих токов и напряжений // Повышение надежности и безопасности трубчатых печей нефтеперерабатывающих и нефтехимических производств: материалы Всероссийского консультационно-методического семинара. – Уфа: Изд-во УГНТУ, 2009. – С. 114–119.

2. Прахов И.В., Баширов М.Г. Влияние режимов работы и характерных повреждений насосно-компрессорного оборудования с электрическим приводом на генерирование высших гармонических составляющих токов и напряжений // Транспорт и хранение нефтепродуктов и углеродного сырья. – 2010. – № 4. – С. 18–21.

3. Прахов И.В., Баширов М.Г., Самородов А.В. Повышение эффективности использования искусственных нейронных сетей в задачах диагностики насосно-компрессорного оборудования применением теории планирования эксперимента // Транспорт и хранение нефтепродуктов и углеводородного сырья. – 2011. – № 2. – С. 14–17.

4. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: пер. с польск. И.Д. Рудинского. – М.: Горячая линия-Телеком, 2007. – 452 с.

5. Терехов В.А. Нейросетевые системы управления: учеб. пособие для вузов / В.А. Терехов, Д.В. Ефимов, И.Ю. Тюкин. – М.: Высшая школа, 2002. – 183 с.

6. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. – М.: Изд-во «Наука», 1976. – 279 с.

В промышленности большая часть поломок машинного оборудования определяется в ненормированной работе электрооборудования, и, как следствие, степень безопасности и надежности технологических процессов во многом зависит от их технического состояния. При максимальных нагрузках, превышенный нормативный срок эксплуатации оборудования, применяемого для переработки нефти и газа, повышает вероятность появления аварийных ситуаций. Применение новых методов и средств диагностики позволит достигнуть высокого уровня промышленной безопасности при физическом и моральном износе насосного оборудования на опасных и вредных промышленных объектах.

Двигатели электропривода при определенных режимах работы, возникновении и развитии повреждений отдельных элементов механической и электрической частей насосного оборудования генерируют характерный спектр гармонических составляющих токов и напряжений прямой, обратной и нулевой последовательностей.

На основании экспериментальных исследований, которые отображают отклонения уровня неисправностей насосного оборудования, в качестве диагностических параметров предложено воспользоваться значениями параметров 3, 5, 7 и 9 гармонических составляющих токов и напряжений – коэффициент гармонических составляющих токов К_In, коэффициент гармонических напряжений К_Un, представляющие собой действующие значения гармонических составляющих, нормированных к действующему значению первой гармоники, и приведенные к периоду значения углов сдвига по фазе φ_ui(n) между соответствующими гармоническими составляющими напряжений и фазных токов.

Метод искусственных нейронных сетей наиболее приемлем для определения уровня поврежденности насосных агрегатов по значениям параметров, создаваемых двигателем электропривода гармоник напряжений и токов [1, 2].

Алгоритм выявления уровня неисправностей насосного оборудования представлен на рис. 1 [3].

Исследуемые ток и напряжение с помощью аналого-цифрового преобразователя «АЦП» преобразуются в цифровой код. Последовательность таких цифровых кодов характеризует сигнал за определённый период времени. Блок дискретного преобразования Фурье «ДПФ» раскладывает исследуемый сигнал на гармонические составляющие, из которых для анализа берутся третья, пятая, седьмая и девятая гармоники. Затем определяются действующие значения коэффициентов гармонических составляющих напряжения К_Un и тока К_In, а также угол между данными величинами φ_ui(n) [3]. Значение показателей режимов работы и поврежденности элементов насосного агрегата D_m является результатом анализа искусственной нейронной сети 1, полученного из значений диагностических параметров, находящихся в пределах нормы.

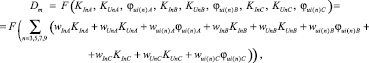(1)

где w – весовые коэффициенты нейронной сети для соответствующих диагностических параметров; m = 1, 2, 3, ..., 17 – число выходов нейронной сети 1.

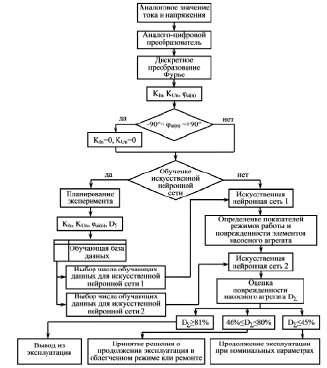
Рис. 1. Алгоритм определения уровня поврежденности насосных агрегатов

В данной работе предложен интегральный диагностический параметр поврежденности D_∑, необходимый для идентификации уровня поврежденности всего насосного агрегата.

Значение интегрального диагностического параметра поврежденности является результатом анализа искусственной нейронной сети 2, полученного из значений показателей режимов работы и поврежденности элементов насосного агрегата D_m.

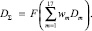(2)

Построение нейросетевой модели происходит адаптивно во время обучения. Для управляемого обучения сети пользователю необходимо организовать систему обучающих данных. Данные параметры показывают модели известных входных и соответствующих им выходных значений. Сеть изучает и пытается установить связь между входами и выходами. Если выходные значения нейронной сети не соответствуют требуемым значениям, то производится оптимизация весов нейронной сети каким-либо из математических алгоритмов до максимального соответствия с заданной точностью. Как показывает практика, сложность возникает в получении необходимого числа обучающих данных. Это является основным недостатком применения искусственных нейронных сетей в задачах диагностики насосного оборудования с электрическим приводом. Увеличение набора обучающих данных и уменьшение числа обучающих экспериментов возможно при обучении искусственной нейронной сети путем использования теории планирования эксперимента [3].

Для определения значений интегрального диагностического параметра поврежденности D_∑ и показателей режимов работы и поврежденности элементов насосного агрегата D_m необходима база данных, основной целью которой является обучение искусственных нейронных сетей.

Для применяемой нейронной сети 1 с количеством входов, равных 36, с 36 нейронами в одном скрытом слое, с числом выходов, равном 17, и с числом настраиваемых весов L = 3204 число экспериментов для обучения, согласно теореме Колмогорова – Арнольда – Хехт – Нильсена [3], должно быть в диапазоне

2(b + L + m) ≤ N ≤ 10(b + L + m); (3)

6514 ≤ N₁ ≤ 32570.

Для применения нейронной сети 2 с количеством входов b, равных 17, с количеством выходов m, равных 1, и с числом настраиваемых весов L = 306 количество обучающих экспериментов должно находиться в диапазоне 612 ≤ N₂ ≤ 3060.

Основной задачей теории планирования эксперимента является определение значений коэффициентов уравнений регрессии, с помощью которых определяется функциональная зависимость выходной величины от воздействующих факторов [6]. В качестве выходной величины используются значения коэффициентов третьей, пятой, седьмой и девятой гармонических составляющих напряжения К_Un и тока К_In и в фазах А, В, С и углы сдвига по фазе φ_ui(n) между ними, а также состояние насосного агрегата, определяемое по параметрам виброускорения прибором ИДП-03. Воздействующими факторами x_n являются различные характерные повреждения и режимы работы насоса.

С помощью уравнения регрессии определяется значение выходной величины при всех возможных сочетаниях уровней факторов, что увеличивает базу обучающих данных искусственной нейронной сети. Число экспериментов, необходимых для создания всех возможных сочетаний уровней факторов, определяется по формуле

N_д = 2^k–р, (4)

где k – число факторов; р – реплика дробного факторного эксперимента; 2 – число уровней.

При числе факторов 17 база данных, согласно формуле (4), увеличивается с 32 до 131072.

Исследовав искусственную нейронную сеть 1 с разными объемами обучающих данных в интервале (6514, 8000, 9000, 10000, 12000,15000, 20000, 25000, 32570), получили зависимость изменения достоверности результата от размера обучающих данных, представленную на рис. 2.

Из рис. 2 видно, что при обеспечении достоверности результата распознавания равной 90,6 % оптимальное количество обучающих данных составляет 12000.

Исследовав искусственную нейронную сеть 2 с разными объемами обучающих данных в интервале (612, 800, 1000, 1500, 2000, 2500, 3060), получили зависимость изменения достоверности результата от размера обучающих данных, представленную на рис. 3.

Из рис. 3 видно, что при обеспечении достоверности результата распознавания равной 86,5 % оптимальное количество обучающих данных составляет 1500.

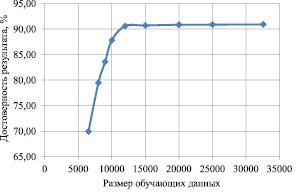
Рис. 2. Зависимость изменения достоверности результата от размера обучающих данных нейронной сети 1

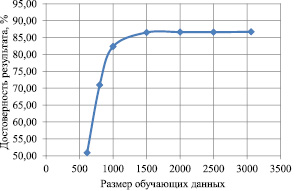
Рис. 3. Зависимость изменения достоверности результата от размера обучающих данных нейронной сети 2

Таким образом, применение метода планирования эксперимента дает возможность сократить необходимое количество обучающих экспериментов для нейронной сети 1 с 12000 до 32 при обеспечении достоверности результата распознавания равной 90,6 %, и для нейронной сети 2 – с 1500 до 32 при обеспечении достоверности результата распознавания, равной 86,5 %.

Рецензенты:

Вильданов Р.Ф., д.т.н., профессор кафедры ЭАПП, филиал ФГБОУ ВПО «Уфимский государственный нефтяной технический университет», г. Салават;

Жирнов Б.С., д.х.н., профессор, зав. кафедрой ХТП, филиал ФГБОУ ВПО «Уфимский государственный нефтяной технический университет», г. Салават.

Библиографическая ссылка