Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Локтионова О.Г. 1 Мальчиков А.В. 1 Яцун А.С. 1

---

1 ФГБОУ ВО «Юго-Западный государственный университет»

Актуальными являются исследования альтернативных принципов движения мобильных роботов, в том числе способов используемых различными животными, например змееподобные и червеподобные походки. В настоящей работе рассматривается способ передвижения трехзвенного робота, имитирующего движение змеи. Изменяемая геометрия корпуса, а также управляемые эффекты взаимодействия робота с поверхностью дают неоспоримые преимущества при движении по неровной и вязкой поверхности. Данные свойства позволяют роботу перемещаться в замкнутых пространствах завалов, трубопроводов, технологических полостях, что открывает большие возможности использования подобного рода аппаратов для поисковых и диагностических задач. В работе приводится описание конструкции трехзвенного робота. Представлено описание математической модели робота, позволяющее исследовать динамические эффекты, возникающие в процессе движения устройства при различных режимах и внешних условиях функционирования. В статье раскрыт принцип движения робототехнических устройств, в основе которого лежит создание управляемых сил трения в точках контакта устройства с поверхностью. Приведены результаты численного моделирования системы, а также анализ полученных результатов, устанавливающих зависимость средней скорости движения устройства от различных параметров системы.

Статья в формате PDF

651 KB

ползающий робот

математическая модель движения робота

управляемые силы трения

1. Черноусько Ф.JI. Движение многозвенника по горизонтальной плоскости // Прикладная математика и механика. – 2000. – Вып. 1. – С. 8–18.

2. Черноусько Ф.Л. О движении трехзвенника по плоскости // Прикладная математика и механика. – 2001. – Т. 65. – Вып. 1. – С. 15–20.

3. Мальчиков А.В. Исследование движения плоского шестизвенного внутритрубного мобильного робота / А.В. Мальчиков, С.Ф. Яцун, С.Б. Рублев // Известия Самарского научного центра Российской академии наук. – Самара, 2012. – № 4 (5). – С. 1263–1265.

4. Сорокин К.С. Управление перемещением трехзвенника на плоскости с трением // Известия РАН. Теория и системы управления. – 2009. – № 3. – С. 165–176.

5. Фигурина Т.Ю. Управляемые квазистатические движения двузвенника по горизонтальной плоскости // Изв. РАН. ТисУ. – 2004. – № 3. – С. 160–176.

6. Локтионова О.Г. Моделирование движения трехзвенного робота с управляемыми силами трения по абсолютно гладкой горизонтальной поверхности / Яцун С.Ф. Рублев С.Б. Волкова Л.Ю., Наумов Г.С. // КубГАУ. – № 91(07). – С. 1–11.

7. Яцун С.Ф. Трехзвенный ползающий робот как средство передвижения / С.Ф. Яцун, Л.Ю. Волкова, С.Б. Рублёв, Г.С. Наумов // Межд. конф. прогресс транспортных средств и систем. – 2013. – С. 293–294.

8. Яцун С.Ф. Автоматизированный мобильный комплекс для диагностики трубопроводов переменного диаметра / С.Ф. Яцун, А.В. Мальчиков // Автоматизация и современные технологии. – М., 2012. – № 12. – С. 3–8.

Одним из путей, позволяющих создать высокоэффективные устройства является копирование движения природных объектов. Особый интерес представляет создание роботов, имитирующих движение змей.

Вопросами проектирования таких устройств занимаются многие ученые, результаты исследования которых отражены в работах [1–5]. В настоящей статье рассматривается робот с возможностью движения за счет создания управляемых сил трения.

Описание робота

Трехзвенный ползающий робот представляет собой три звена 1, 2, 3 соединенных посредством шарниров 4, оснащенных поворотными сервоприводами.

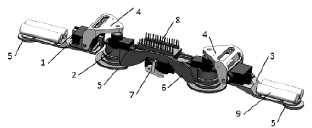
Рис. 1. Ползающий трехзвенный робот

Шарнир 4 позволяет осуществлять смещение боковых звеньев как в горизонтальной, так и в вертикальной плоскости, что обеспечивает изменение конфигурации корпуса устройства в зависимости от используемого режима перемещения.

Подъем и опускание боковых звеньев позволяет скомпенсировать неровность поверхности. Смещения звеньев в горизонтальной плоскости позволяют реализовывать продольные, поперечные, а также смешанные походки.

На каждом звене установлены фрикционные опоры 5, посредством которых робот взаимодействует с поверхностью. Центральное звено 2 оснащено системой управления величиной силы трения. Изменение силы трения осуществляется путем введения в контактирующую зону дополнительной опорной поверхности 6 с фрикционным покрытием, обеспечивающим более высокую силу трения робота с поверхностью. Робот имеет плату управления 8, закрепленную на корпусе, а также элементы питания 9, обеспечивающие автономную работу устройства. Механизм изменения типа опорной поверхности 7 показан на рис. 2.

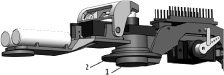
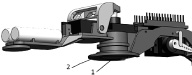
а б

Рис. 2. Опора центрального звена: а – контакт с поверхностью осуществляется стационарной опорой 1; б – контакт осуществляется дополнительной опорной поверхностью 2

Математическая модель трехзвенного робота

Для разработки математической модели рассмотрим расчетную схему, показанную на рис. 3. Положим, что каждое звено робота i = 1–3 является абсолютно твердым стержнем O_iO_i+1 длиной l_i и массой m_i, центр масс которого совпадает с центром симметрии С_i. На данном этапе исследований будем считать, что шарниры, обеспечивающие вращение звеньев в горизонтальной и вертикальной плоскостях, конструктивно располагаются на небольших расстояниях друг от друга, поэтому на расчетной схеме робота они совмещаются и располагаются в точках О₂ и О₃.

Движение устройства происходит в неподвижной абсолютной системе координат Оxyz. Для описания кинематики и динамики объекта с точками О_i, i = 1–3 звеньев связаны относительные системы координат О_ix_iy_iz_i, повернутые на углы φ_i относительно оси Оz, и 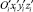, повернутые на углы θ_i относительно осей О_iу_i. Положительные направления углов отсчитываются против часовой стрелки от осей Ох и О_ix_i соответственно. Будем считать, что движение робота происходит по горизонтальной шероховатой поверхности.

В работе рассматривается такое движение устройства, при котором опорные элементы звена 2 всегда взаимодействуют с поверхностью. Это приводит к тому, что системы координат О₂x₂y₂z₂ и 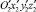совпадают. Звенья 1 и 3 могут находиться на поверхности и контактировать с ней, а могут быть подняты относительно плоскости Оху.

Движение робота по поверхности происходит за счет моментов М_1z, M_3z, обеспечивающих поворот звеньев 1 и 3 относительно звена 2 в горизонтальной плоскости, и моментов М_1y, M_3y, посредством которых указанные звенья вращаются в вертикальной плоскости, а также за счет сил трения, возникающих при взаимодействии опор с поверхностью.

Контакт робота с поверхностью осуществляется в точках O_i, i = 1–4, являющихся крайними точками звеньев. При этом возникают силы трения F_fri, направленные противоположно векторам скоростей указанных точек и описываемые моделью сухого трения.

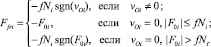
где F_0i – горизонтальная проекция равнодействующей всех сил, кроме силы сухого трения, приложенных к точке контакта; f – коэффициент трения скольжения; N_i – нормальная реакция в точке O_i; v_Oi – скорость точки O_i [6–8].

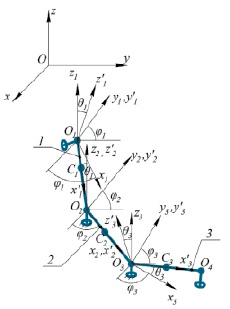
Рис. 3. Расчетная схема робота

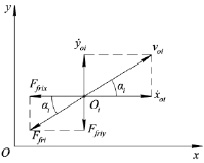
Рис. 4. Схема приложения сил трения в контактных точках

Нормальные реакции в опорных точках при взаимодействии четырех контактных элементов с поверхностью равны

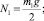
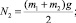
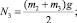
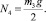
При двух опорах имеем

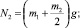
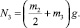
Проекции силы трения на оси Ох и Оу абсолютной системы координат определяются по формулам

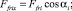
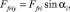
где 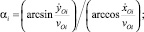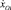, 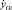– проекции скорости точки О_i на оси Ох и Оу.

Коэффициент трения между опорой и поверхностью является управляемой величиной и обусловлен изменением фрикционных свойств опорных элементов за счет использования различных материалов. В работе рассматривается один из возможных вариантов перемещения робота – змееподобное движение – при котором отрыва опорных элементов звеньев 1 и 3 от поверхности не происходит. Это позволяет от пространственной задачи перейти к плоской и рассмотреть движение устройства по горизонтальной шероховатой поверхности, совпадающей с плоскостью Оху. Движение устройства представлено в виде последовательности пяти этапов, на каждом из них поведение объекта описывается своими дифференциальными уравнениями с учетом накладываемых связей.

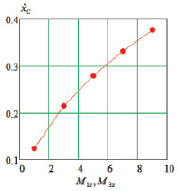
а б

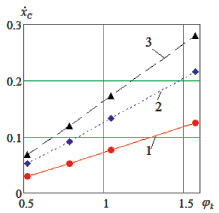
Рис. 5. График зависимостей: а – 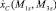при φ_k = π/2; б – 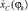при M_1z = M_3z = 1 Нм; 2 – M_1z = M_3z = 3 Nm; 3 – M_1z = M_3z = 1 Нм

Для обобщения результатов моделирования на рис. 5 представлены графики средней скорости 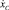перемещения робота вдоль оси Ох от значений угла φ_k и моментов, создаваемых приводами. Средняя скорость вычисляется как отношение расстояния, пройденного центром масс объекта за один цикл (пять этапов), ко времени цикла.

На рис. 5, б видно, что с увеличением значений угла φ_k средняя скорость движения робота возрастает по пропорциональному закону, причем коэффициент пропорциональности растет по мере роста φ_k.

График, представленный на рис. 5, б, позволяет сделать вывод о том, что средняя скорость устройства почти пропорциональна моментам приводов, обеспечивающих относительное движение звеньев.

Выводы

В статье предложена конструкция робота, имитирующего движение змеи, отличительной особенностью которого является управляемое трение в точках контакта робота с поверхностью. Разработана математическая модель движения робота, позволяющая рассчитать мгновенные значения скоростей точек звеньев робота, а также величину средней скорости робота в зависимости от величины управляющих моментов. Установлено, что скорость практически пропорционально зависит от максимального угла поворота звеньев механизма и величины управляющих моментов.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № № 13-08-00795 а.

Рецензенты:

Кобелев Н.С., д.т.н., профессор, заведующий кафедрой теплогазоснабжения и вентиляции, ФГБОУ ВПО «Юго-Западный государственный университет», г. Курск;

Шевякин В.Н., д.т.н., профессор, ФГБОУ ВПО «Юго-Западный государственный университет», г. Курск.

Библиографическая ссылка